物联网安全himqtt防火墙数据结构之红黑树源码分析
物联网安全himqtt防火墙数据结构之红黑树源码分析
随着5G的发展，物联网安全显得特别重要，himqtt是首款完整源码的高性能MQTT物联网防火墙 - MQTT Application FireWall，C语言编写，采用epoll模式支持IoT数十万的高并发连接，并且兼容ModSecurity部分规则。 代码非常优秀，非常值得收藏和学习。
红黑树是一种特殊的自平衡二叉树数据结构，其自旋和左旋乃天才的设计，linux内核中大量使用。阿里巴巴面试非常看重红黑树，因为从几十万的数据中，用短短的几步就可能查到所要的数据，其原理教程网上很多，今天我们从首款物联网防火墙himqtt里面上分析红黑树源码。
首先在github上下载himqtt的源码：https://github.com/qq4108863/himqtt
找到src目录下的mqtt_rbtree.c和mqtt_rbtree.h文件，结构图如下：
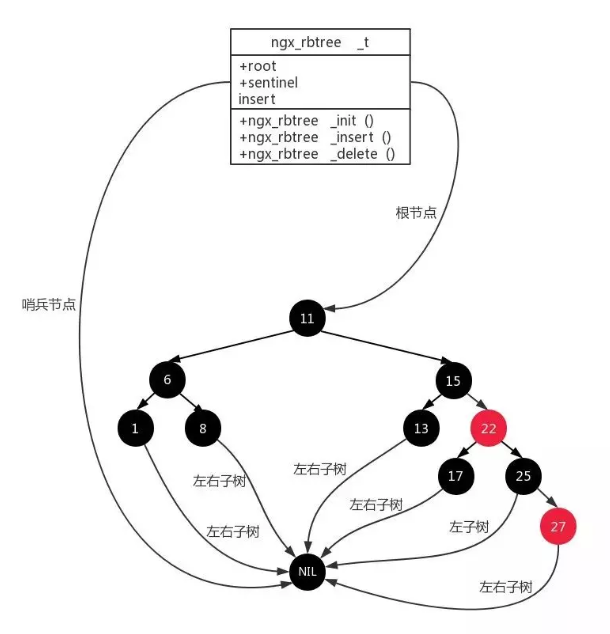
1、结构体
typedef ngx_uint_t ngx_rbtree_key_t;
typedef ngx_int_t ngx_rbtree_key_int_t;
/* 红黑树节点结构 */
typedef struct ngx_rbtree_node_s ngx_rbtree_node_t;
struct ngx_rbtree_node_s {
ngx_rbtree_key_t key; /* 节点的键值 */
ngx_rbtree_node_t *left; /* 节点的左孩子 */
ngx_rbtree_node_t *right; /* 节点的右孩子 */
ngx_rbtree_node_t *parent; /* 节点的父亲 */
u_char color; /* 节点的颜色 */
u_char data; /* */};
typedef struct ngx_rbtree_s ngx_rbtree_t;
typedef void (*ngx_rbtree_insert_pt) (ngx_rbtree_node_t *root,
ngx_rbtree_node_t *node, ngx_rbtree_node_t *sentinel);
/* 红黑树结构 */
struct ngx_rbtree_s {
ngx_rbtree_node_t *root; /* 指向树的根节点 */
ngx_rbtree_node_t *sentinel;/* 指向树的叶子节点NIL */
ngx_rbtree_insert_pt insert; /* 添加元素节点的函数指针，解决具有相同键值，但不同颜色节点的冲突问题；
* 该函数指针决定新节点的行为是新增还是替换原始某个节点*/};
2、初始化
/* 给节点着色，1表示红色，0表示黑色 */
#define ngx_rbt_red(node) ((node)->color = 1)
#define ngx_rbt_black(node) ((node)->color = 0)/* 判断节点的颜色 */
#define ngx_rbt_is_red(node) ((node)->color)
#define ngx_rbt_is_black(node) (!ngx_rbt_is_red(node))/* 复制某个节点的颜色 */
#define ngx_rbt_copy_color(n1, n2) (n1->color = n2->color)
/* 节点着黑色的宏定义 *//* a sentinel must be black */
#define ngx_rbtree_sentinel_init(node) ngx_rbt_black(node)
/* 初始化红黑树，即为空的红黑树 *//* tree 是指向红黑树的指针，
* s 是红黑树的一个NIL节点，
* i 表示函数指针，决定节点是新增还是替换
*/
#define ngx_rbtree_init(tree, s, i) \
ngx_rbtree_sentinel_init(s); \
(tree)->root = s; \
(tree)->sentinel = s; \
(tree)->insert = i
3、天才的左旋和右旋
/* 左旋转操作 */
static ngx_inline voidngx_rbtree_left_rotate(ngx_rbtree_node_t **root, ngx_rbtree_node_t *sentinel,
ngx_rbtree_node_t *node){
ngx_rbtree_node_t *temp;
/*
| |
x y
/ \ / \
a y ---left---> x c
/ \ / \
b c a b
*/
/*node = x*/
temp = node->right;/* temp为node节点的右孩子 */
node->right = temp->left;/* 设置node节点的右孩子为temp的左孩子 */
if (temp->left != sentinel) {
temp->left->parent = node;
}
temp->parent = node->parent;
if (node == *root) {
*root = temp;
} else if (node == node->parent->left) {
node->parent->left = temp;
} else {
node->parent->right = temp;
}
temp->left = node;
node->parent = temp;}
/* 右旋转操作 */
static ngx_inline voidngx_rbtree_right_rotate(ngx_rbtree_node_t **root, ngx_rbtree_node_t *sentinel,
ngx_rbtree_node_t *node){
ngx_rbtree_node_t *temp;
/*
| |
x y
/ \ / \
a y <---right-- x c
/ \ / \
b c a b
*/
/*node = y*/
temp = node->left;
node->left = temp->right;
if (temp->right != sentinel) {
temp->right->parent = node;
}
temp->parent = node->parent;
if (node == *root) {
*root = temp;
} else if (node == node->parent->right) {
node->parent->right = temp;
} else {
node->parent->left = temp;
}
temp->right = node;
node->parent = temp;}
/* 获取红黑树键值最小的节点 */
static ngx_inline ngx_rbtree_node_t *ngx_rbtree_min(ngx_rbtree_node_t *node, ngx_rbtree_node_t *sentinel){
while (node->left != sentinel) {
node = node->left;
}
return node;}
/* 插入节点 *//* 插入节点的步骤：
* 1、首先按照二叉查找树的插入操作插入新节点；
* 2、然后把新节点着色为红色（避免破坏红黑树性质5）；
* 3、为维持红黑树的性质，调整红黑树的节点（着色并旋转），使其满足红黑树的性质；
*/
4、插入值
voidngx_rbtree_insert(ngx_thread_volatile ngx_rbtree_t *tree,
ngx_rbtree_node_t *node){
ngx_rbtree_node_t **root, *temp, *sentinel;
/* a binary tree insert */
root = (ngx_rbtree_node_t **) &tree->root;
sentinel = tree->sentinel;
/* 若红黑树为空，则比较简单，把新节点作为根节点，
* 并初始化该节点使其满足红黑树性质
*/
if (*root == sentinel) {
node->parent = NULL;
node->left = sentinel;
node->right = sentinel;
ngx_rbt_black(node);
*root = node;
return;
}
/* 若红黑树不为空，则按照二叉查找树的插入操作进行
* 该操作由函数指针提供
*/
tree->insert(*root, node, sentinel);
/* re-balance tree */
/* 调整红黑树，使其满足性质，
* 其实这里只是破坏了性质4：若一个节点是红色，则孩子节点都为黑色；
* 若破坏了性质4，则新节点 node 及其父亲节点 node->parent 都为红色；
*/
while (node != *root && ngx_rbt_is_red(node->parent)) {
/* 若node的父亲节点是其祖父节点的左孩子 */
if (node->parent == node->parent->parent->left) {
temp = node->parent->parent->right;/* temp节点为node的叔叔节点 */
/* case1：node的叔叔节点是红色 */
/* 此时，node的父亲及叔叔节点都为红色；
* 解决办法：将node的父亲及叔叔节点着色为黑色，将node祖父节点着色为红色；
* 然后沿着祖父节点向上判断是否会破会红黑树的性质；
*/
if (ngx_rbt_is_red(temp)) {
ngx_rbt_black(node->parent);
ngx_rbt_black(temp);
ngx_rbt_red(node->parent->parent);
node = node->parent->parent;
} else {
/* case2：node的叔叔节点是黑色且node是父亲节点的右孩子 */
/* 则此时，以node父亲节点进行左旋转，使case2转变为case3；
*/
if (node == node->parent->right) {
node = node->parent;
ngx_rbtree_left_rotate(root, sentinel, node);
}
/* case3：node的叔叔节点是黑色且node是父亲节点的左孩子 */
/* 首先，将node的父亲节点着色为黑色，祖父节点着色为红色；
* 然后以祖父节点进行一次右旋转；
*/
ngx_rbt_black(node->parent);
ngx_rbt_red(node->parent->parent);
ngx_rbtree_right_rotate(root, sentinel, node->parent->parent);
}
} else {/* 若node的父亲节点是其祖父节点的右孩子 */
/* 这里跟上面的情况是对称的，就不再进行讲解了
*/
temp = node->parent->parent->left;
if (ngx_rbt_is_red(temp)) {
ngx_rbt_black(node->parent);
ngx_rbt_black(temp);
ngx_rbt_red(node->parent->parent);
node = node->parent->parent;
} else {
if (node == node->parent->left) {
node = node->parent;
ngx_rbtree_right_rotate(root, sentinel, node);
}
ngx_rbt_black(node->parent);
ngx_rbt_red(node->parent->parent);
ngx_rbtree_left_rotate(root, sentinel, node->parent->parent);
}
}
}
/* 根节点必须为黑色 */
ngx_rbt_black(*root);}
/* 这里只是将节点插入到红黑树中，并没有判断是否满足红黑树的性质；
* 类似于二叉查找树的插入操作，这个函数为红黑树插入操作的函数指针；
*/
voidngx_rbtree_insert_value(ngx_rbtree_node_t *temp, ngx_rbtree_node_t *node,
ngx_rbtree_node_t *sentinel){
ngx_rbtree_node_t **p;
for ( ;; ) {
/* 判断node节点键值与temp节点键值的大小，以决定node插入到temp节点的左子树还是右子树 */
p = (node->key < temp->key) ? &temp->left : &temp->right;
if (*p == sentinel) {
break;
}
temp = *p;
}
/* 初始化node节点，并着色为红色 */
*p = node;
node->parent = temp;
node->left = sentinel;
node->right = sentinel;
ngx_rbt_red(node);}
voidngx_rbtree_insert_timer_value(ngx_rbtree_node_t *temp, ngx_rbtree_node_t *node,
ngx_rbtree_node_t *sentinel){
ngx_rbtree_node_t **p;
for ( ;; ) {
/*
* Timer values
* 1) are spread in small range, usually several minutes,
* 2) and overflow each 49 days, if milliseconds are stored in 32 bits.
* The comparison takes into account that overflow.
*/
/* node->key < temp->key */
p = ((ngx_rbtree_key_int_t) (node->key - temp->key) < 0)
? &temp->left : &temp->right;
if (*p == sentinel) {
break;
}
temp = *p;
}
*p = node;
node->parent = temp;
node->left = sentinel;
node->right = sentinel;
ngx_rbt_red(node);}
5、删除值
/* 删除节点 */
voidngx_rbtree_delete(ngx_thread_volatile ngx_rbtree_t *tree,
ngx_rbtree_node_t *node){
ngx_uint_t red;
ngx_rbtree_node_t **root, *sentinel, *subst, *temp, *w;
/* a binary tree delete */
root = (ngx_rbtree_node_t **) &tree->root;
sentinel = tree->sentinel;
/* 下面是获取temp节点值，temp保存的节点是准备替换节点node ；
* subst是保存要被替换的节点的后继节点；
*/
/* case1：若node节点没有左孩子（这里包含了存在或不存在右孩子的情况）*/
if (node->left == sentinel) {
temp = node->right;
subst = node;
} else if (node->right == sentinel) {/* case2：node节点存在左孩子，但是不存在右孩子 */
temp = node->left;
subst = node;
} else {/* case3：node节点既有左孩子，又有右孩子 */
subst = ngx_rbtree_min(node->right, sentinel);/* 获取node节点的后续节点 */
if (subst->left != sentinel) {
temp = subst->left;
} else {
temp = subst->right;
}
}
/* 若被替换的节点subst是根节点，则temp直接替换subst称为根节点 */
if (subst == *root) {
*root = temp;
ngx_rbt_black(temp);
/* DEBUG stuff */
node->left = NULL;
node->right = NULL;
node->parent = NULL;
node->key = 0;
return;
}
/* red记录subst节点的颜色 */
red = ngx_rbt_is_red(subst);
/* temp节点替换subst 节点 */
if (subst == subst->parent->left) {
subst->parent->left = temp;
} else {
subst->parent->right = temp;
}
/* 根据subst是否为node节点进行处理 */
if (subst == node) {
temp->parent = subst->parent;
} else {
if (subst->parent == node) {
temp->parent = subst;
} else {
temp->parent = subst->parent;
}
/* 复制node节点属性 */
subst->left = node->left;
subst->right = node->right;
subst->parent = node->parent;
ngx_rbt_copy_color(subst, node);
if (node == *root) {
*root = subst;
} else {
if (node == node->parent->left) {
node->parent->left = subst;
} else {
node->parent->right = subst;
}
}
if (subst->left != sentinel) {
subst->left->parent = subst;
}
if (subst->right != sentinel) {
subst->right->parent = subst;
}
}
/* DEBUG stuff */
node->left = NULL;
node->right = NULL;
node->parent = NULL;
node->key = 0;
if (red) {
return;
}
/* 下面开始是调整红黑树的性质 */
/* a delete fixup */
/* 根据temp节点进行处理 ，若temp不是根节点且为黑色 */
while (temp != *root && ngx_rbt_is_black(temp)) {
/* 若temp是其父亲节点的左孩子 */
if (temp == temp->parent->left) {
w = temp->parent->right;/* w为temp的兄弟节点 */
/* case A：temp兄弟节点为红色 */
/* 解决办法：
* 1、改变w节点及temp父亲节点的颜色；
* 2、对temp父亲节的做一次左旋转，此时，temp的兄弟节点是旋转之前w的某个子节点，该子节点颜色为黑色；
* 3、此时，case A已经转换为case B、case C 或 case D；
*/
if (ngx_rbt_is_red(w)) {
ngx_rbt_black(w);
ngx_rbt_red(temp->parent);
ngx_rbtree_left_rotate(root, sentinel, temp->parent);
w = temp->parent->right;
}
/* case B：temp的兄弟节点w是黑色，且w的两个子节点都是黑色 */
/* 解决办法：
* 1、改变w节点的颜色；
* 2、把temp的父亲节点作为新的temp节点；
*/
if (ngx_rbt_is_black(w->left) && ngx_rbt_is_black(w->right)) {
ngx_rbt_red(w);
temp = temp->parent;
} else {/* case C：temp的兄弟节点是黑色，且w的左孩子是红色，右孩子是黑色 */
/* 解决办法：
* 1、将改变w及其左孩子的颜色；
* 2、对w节点进行一次右旋转；
* 3、此时，temp新的兄弟节点w有着一个红色右孩子的黑色节点，转为case D；
*/
if (ngx_rbt_is_black(w->right)) {
ngx_rbt_black(w->left);
ngx_rbt_red(w);
ngx_rbtree_right_rotate(root, sentinel, w);
w = temp->parent->right;
}
/* case D：temp的兄弟节点w为黑色，且w的右孩子为红色 */
/* 解决办法：
* 1、将w节点设置为temp父亲节点的颜色，temp父亲节点设置为黑色；
* 2、w的右孩子设置为黑色；
* 3、对temp的父亲节点做一次左旋转；
* 4、最后把根节点root设置为temp节点；*/
ngx_rbt_copy_color(w, temp->parent);
ngx_rbt_black(temp->parent);
ngx_rbt_black(w->right);
ngx_rbtree_left_rotate(root, sentinel, temp->parent);
temp = *root;
}
} else {/* 这里针对的是temp节点为其父亲节点的左孩子的情况 */
w = temp->parent->left;
if (ngx_rbt_is_red(w)) {
ngx_rbt_black(w);
ngx_rbt_red(temp->parent);
ngx_rbtree_right_rotate(root, sentinel, temp->parent);
w = temp->parent->left;
}
if (ngx_rbt_is_black(w->left) && ngx_rbt_is_black(w->right)) {
ngx_rbt_red(w);
temp = temp->parent;
} else {
if (ngx_rbt_is_black(w->left)) {
ngx_rbt_black(w->right);
ngx_rbt_red(w);
ngx_rbtree_left_rotate(root, sentinel, w);
w = temp->parent->left;
}
ngx_rbt_copy_color(w, temp->parent);
ngx_rbt_black(temp->parent);
ngx_rbt_black(w->left);
ngx_rbtree_right_rotate(root, sentinel, temp->parent);
temp = *root;
}
}
}
ngx_rbt_black(temp);}
红黑树比较复杂，但根本不用程序员自己编写，直接用就可以了，himqtt的红黑树也是来源于nginx的数据结构，非常感谢那些开源大神，有了github，人类的知识和智慧进一步得以传承。
作为程序员，会copy优秀的代码也是一种非常重要的能力，大家不用再面向你的对象编程，面向github就行了。
物联网安全himqtt防火墙数据结构之红黑树源码分析的更多相关文章
- HashMap中的TreeNode，红黑树源码分析
在看HashMap的源码时候看到了TreeNode.因此需要对其进行一个了解.是一个红黑树.可以百度一下红黑树的数据结构.分析了下源码,还是比较枯燥的 红黑树的性质:本身是一个二叉查找树(所有左节点的 ...
- 物联网安全himqtt防火墙数据结构之ringbuffer环形缓冲区
物联网安全himqtt防火墙数据结构之ringbuffer环形缓冲区 随着5G的普及,物联网安全显得特别重要,himqtt是首款完整源码的高性能MQTT物联网防火墙 - MQTT Applicatio ...
- Linux 内核里的数据结构：红黑树（rb-tree）
转自:https://www.cnblogs.com/slgkaifa/p/6780299.html 作为一种数据结构.红黑树可谓不算朴素.由于各种宣传让它过于神奇,网上搜罗了一大堆的关于红黑树的文章 ...
- Java HashMap源码分析（含散列表、红黑树、扰动函数等重点问题分析）
写在最前面 这个项目是从20年末就立好的 flag,经过几年的学习,回过头再去看很多知识点又有新的理解.所以趁着找实习的准备,结合以前的学习储备,创建一个主要针对应届生和初学者的 Java 开源知识项 ...
- 【数据结构】8.java源码关于HashMap
1.hashmap的底层数据结构 众所皆知map的底层结构是类似邻接表的结构,但是进入1.8之后,链表模式再一定情况下又会转换为红黑树在JDK8中,当链表长度达到8,并且hash桶容量超过64(MIN ...
- 【数据结构】9.java源码关于HashTable
1.hashtable的内部结构 基础存储数据的hash桶由Entry结构的数组存放而entry数据结构,有hash,key和value,还有一个指向下一个节点的引用next对象 这里就和hashma ...
- HDFS源码分析心跳汇报之数据结构初始化
在<HDFS源码分析心跳汇报之整体结构>一文中,我们详细了解了HDFS中关于心跳的整体结构,知道了BlockPoolManager.BPOfferService和BPServiceActo ...
- 【数据结构】红黑树与跳表-(SortSet)-(TreeMap)-(TreeSet)
SortSet 有序的Set,其实在Java中TreeSet是SortSet的唯一实现类,内部通过TreeMap实现的:而TreeMap是通过红黑树实现的:而在Redis中是通过跳表实现的: Skip ...
- Java数据结构和算法 - TreeMap源码理解红黑树
前言 本篇将结合JDK1.6的TreeMap源码,来一起探索红-黑树的奥秘.红黑树是解决二叉搜索树的非平衡问题. 当插入(或者删除)一个新节点时,为了使树保持平衡,必须遵循一定的规则,这个规则就是红- ...
随机推荐
- App元素定位
1.元素定位(采用Appium-desktop自带的工具) 1.1将初始化参数复制进去校验json格式正确且保存后,点击start session 初始化参数来源如下: # 定义启动设备需要的参数 d ...
- 面试必备：高频算法题终章「图文解析 + 范例代码」之 矩阵 二进制 + 位运算 + LRU 合集
Attention 秋招接近尾声,我总结了 牛客.WanAndroid 上,有关笔试面经的帖子中出现的算法题,结合往年考题写了这一系列文章,所有文章均与 LeetCode 进行核对.测试.欢迎食用 本 ...
- feof() 函数判断不准确的问题
大家在读文件时应该碰到过这样的问题,while(!feof(fp)) 函数在读文件时会多循环一次,导致 fscanf() 函数多读了一次文件. 所以也就在输出的时候会产生一些乱码. 可以看看下面的代码 ...
- [BZOJ1415][NOI2005]聪聪与可可
Description Input 数据的第1行为两个整数N和E,以空格分隔,分别表示森林中的景点数和连接相邻景点的路的条数. 第2行包含两个整数C和M,以空格分隔,分别表示初始时聪聪和可可所在的景点 ...
- python类中的self
class User: def walk(self): print(self,"正在慢慢走") # User.walk() # 会报错 TypeError: walk() miss ...
- 图像处理 - ImageMagick 简单介绍与案例
在客户端我们可以用 PhotoShop 等 GUI 工具处理静态图片或者动态 GIF 图片,不过在服务器端对于 WEB 应用程序要处理图片格式转换,缩放裁剪,翻转扭曲,PDF解析等操作, GUI 软件 ...
- 关于M23内核简介 - 待续
1.定位 M23是基于最新的ARMv8-M构架的主要关注低功耗应用的微控制器,未来会是M0.M0+的替代品. M33是基于最新的ARMv8-M构架的主要关注高能效应用的微控制器,未来会替换M3.M4. ...
- Mongodb 常见的查询语句及与 mysql 对比
db.users.find()select * from users db.users.find({"age" : 27})select * from users where ag ...
- vue-class-component使用Mixins
vue-class-component提供了mixinshelper函数,以类样式的方式使用mixins.通过使用mixins帮助程序,TypeScript可以推断mixin类型并在组件类型上继承它们 ...
- 斯坦福机器学习课程 Exercise 习题三
Exercise 3: Multivariate Linear Regression 预处理数据 Preprocessing the inputs will significantly increas ...