C语言程序设计100例之（25）：确定进制

例25 确定进制

问题描述

6*9 = 42 对于十进制来说是错误的，但是对于13进制来说是正确的。即

6（13）* 9（13）= 42（13），因为，在十三进制中，42 = 4 * 13 + 2 = 54（10）。

编写一个程序，输入三个整数p、q和r，然后确定一个进制B（2<=B<=16），使得在该进制下 p * q = r。如果 B有很多选择，输出最小的一个。例如，p = 11，q = 11，r = 121。则有 11（3） * 11（3）= 121（3），还有 11（10）* 11（10）= 121（10）。这种情况下，输出3。如果没有合适的进制，则输出0。

输入格式

三个整数p、q和r。

输出格式

所确定的进制B。如果没有合适的进制，则输出0。

输入样例

6 9 42

输出样例

（1）编程思路。

选择一个进制B，按照该进制将被乘数p、乘数q、乘积r分别转换成十进制数pb、qb和rb。然后判断等式pb*qb==rb是否成立。使得等式成立的最小B就是所求的结果。

设n位B进制数num=（a_n-1a_n-2……a₁a₀），将其按权值展开后求和就可得到对应的十进制数ret。

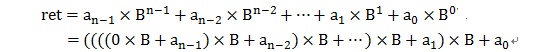
由上式可以看出，B进制数num转换为十进制数ret可以写成一个循环。方法是：另ret初始值为0，从高位到低位循环分离出num的各位数字digit，执行 ret=ret*b+digit，循环结束就可得B进制数num对应的十进制数ret。

编写函数int b2ten(int num,int b)完成b进制数num转换为十进制数。

由于转换时需要从高位向低位分离数字，而用循环

while (num!=0)

{

digit = num%10;

num = num/10;

}

能方便地完成从低位向高位分离出num的各位数字。因此，可采用一个数组digit[]来保存从低位向高位分离出的各位数字，同时num中数字的位数保存到变量cnt中。

（2）源程序。

#include <stdio.h>

int b2ten(int num,int b);

int main()

{

int b,p,r,q;

int pb,qb,rb; // 用来存储转换为十进制后的结果

scanf("%d%d%d",&p,&q,&r);

for(b=2;b<=16;b++)

{

pb=b2ten(p,b);

qb=b2ten(q,b);

rb=b2ten(r,b);

if(pb==-1 || qb==-1 || rb==-1) continue;

if (pb*qb==rb)

{

printf("%d\n",b);

break;

}

if(b==17)

printf("0\n");

return 0;

}

int b2ten(int num,int b)

{

int ret=0,digit[10];

int cnt=0;

while (num!=0)

{

digit[cnt++]=num%10;

num=num/10;

}

cnt--;

while (cnt>=0)

{

if (digit[cnt]>=b) return -1; // 数字超过B进制的数码范围

ret=ret*b+digit[cnt];

cnt--;

}

return ret;

}

习题25

25-1 Faulty Odometer

本题选自北大POJ题库（http://poj.org/problem?id=2719）。

Description

You are given a car odometer which displays the miles traveled as an integer. The odometer has a defect, however: it proceeds from the digit 3 to the digit 5, always skipping over the digit 4. This defect shows up in all positions (the one's, the ten's, the hundred's, etc.). For example, if the odometer displays 15339 and the car travels one mile, odometer reading changes to 15350 (instead of 15340).

Input

Each line of input contains a positive integer in the range 1..999999999 which represents an odometer reading. (Leading zeros will not appear in the input.) The end of input is indicated by a line containing a single 0. You may assume that no odometer reading will contain the digit 4.

Output

Each line of input will produce exactly one line of output, which will contain: the odometer reading from the input, a colon, one blank space, and the actual number of miles traveled by the car.

Sample Input

2003

2005

239

250

1399

1500

999999

Sample Output

13: 12

15: 13

2003: 1461

2005: 1462

239: 197

250: 198

1399: 1052

1500: 1053

999999: 531440

（1）编程思路。

本题的题意是：有一个里程表，表盘上的数字4坏了，因此所有的数字4无法显示，3之后显示5，39之后显示50，…。先给出里程表上显示的数字，求实际的里程应为多少？

由于里程表上无数字4，因此可以将里程表上的数看成是一个9进制数，有0,1,2,3,5,6,7,8,9共9个数码，规则逢九进一。因此本题实质是将一个9进制数转换为一个十进制数。

（2）源程序。

#include <stdio.h>

int main()

{

char odometer[10];

int actual,i,d;

while(scanf("%s",odometer) && odometer[0]!='0')

{

actual=0;

for (i=0;odometer[i]!='\0';i++)

{

d=odometer[i]-'0';

if (d>3) d--;

actual=actual*9+d;

}

printf("%s: %d\n",odometer,actual);

}

return 0;

}

25-2 Skew Binary

本题选自北大POJ题库（http://poj.org/problem?id=1565）。

Description

When a number is expressed in decimal, the kth digit represents a multiple of 10k. (Digits are numbered from right to left, where the least significant digit is number 0.) For example,

81307(10) = 8 * 10^4 + 1 * 10 ^3 + 3 * 10^2 + 0 * 10^1 + 7 * 10^0

= 80000 + 1000 + 300 + 0 + 7

= 81307.

When a number is expressed in binary, the kth digit represents a multiple of 2^k . For example,

10011(2) = 1 * 2^4 + 0 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0

= 16 + 0 + 0 + 2 + 1

= 19.

In skew binary, the kth digit represents a multiple of 2^(k+1)-1. The only possible digits are 0 and 1, except that the least-significant nonzero digit can be a 2. For example,

10120(skew) = 1 * (2^5-1) + 0 * (2^4-1) + 1 * (2^3-1) + 2 * (2^2-1) + 0 * (2^1-1)

= 31 + 0 + 7 + 6 + 0

= 44.

The first 10 numbers in skew binary are 0, 1, 2, 10, 11, 12, 20, 100, 101, and 102. (Skew binary is useful in some applications because it is possible to add 1 with at most one carry. However, this has nothing to do with the current problem.)

Input

The input contains one or more lines, each of which contains an integer n. If n = 0 it signals the end of the input, and otherwise n is a nonnegative integer in skew binary.

Output

For each number, output the decimal equivalent. The decimal value of n will be at most 2^31-1 = 2147483647.

Sample Input

10120

200000000000000000000000000000

1000000000000000000000000000000

100

11111000001110000101101102000

Sample Output

2147483646

2147483647

1041110737

（1）编程思路。

按题目描述中给出的展开式进行展开计算即可。

（2）源程序。

#include <stdio.h>

#include <string.h>

int main()

{

char bin[33];

int i,value,p;

while (scanf("%s",bin) && strcmp(bin,"0")!=0)

{

p=1; value=0;

for (i=strlen(bin)-1;i>=0;i--)

{

p=p*2;

value+=(bin[i]-'0')*(p-1);

}

printf("%d\n",value);

}

return 0;

}

25-3 数列

本题选自洛谷题库（https://www.luogu.org/problem/P1062）。

题目描述

给定一个正整数k(3≤k≤15)，把所有k的方幂及所有有限个互不相等的k的方幂之和构成一个递增的序列，例如，当k=3，时，这个序列是：1,3,4,9,10,12,13,…

（该序列实际上就是：3^0,3^1,3^0+3^1,3^2,3^0+3^2,3^1+3^2,3^0+3^1+3^2,…）

请你求出这个序列的第N项的值（用10进制数表示）。

例如，对于k=3，N=100，正确答案应该是981。

输入格式

2个正整数，用一个空格隔开：

k N（k、N的含义与上述的问题描述一致，且3≤k≤15,10≤N≤1000）。

输出格式

1个正整数。

输入样例

3 100

输出样例

981

（1）编程思路。

先分析样例

k=3时，数列为：1,3,4,9,10,12,13，…

转换成三进制就是：1,10,11,100,101,110,111，…

看起来像是二进制，转化成十进制就是：1,2,3,4,5,6,7，…

显然，第n项就是n。

编写一个程序，把上面的过程逆回去，即先把n转换成二进制，再把它当成K进制，重新转换为十进制，就可以得到结果。

（2）源程序1。

#include <stdio.h>

int main()

{

int a[11]={0},k,n,cnt,i;

scanf("%d%d",&k,&n);

cnt=0;

while (n!=0)

{

a[cnt++]=n%2;

n/=2;

}

long long s=0;

for (i=cnt-1;i>=0;i--)

s=s*k+a[i];

printf("%lld\n",s);

return 0;

}

（3）源程序2。

#include <stdio.h>

int main()

{

int k,n;

scanf("%d%d",&k,&n);

long long s=0,p=1;

while (n!=0)

{

s=s+(n%2)*p;

p*=k;

n/=2;

}

printf("%lld\n",s);

return 0;

}