LeetCode刷题总结-数组篇（上）

数组是算法中最常用的一种数据结构，也是面试中最常考的考点。在LeetCode题库中，标记为数组类型的习题到目前为止，已累计到了202题。然而，这202道习题并不是每道题只标记为数组一个考点，大部分习题都有两到三个考点。比如，考查数组+哈希表、数组+动态规划+数学、数组+回溯等。

看到如此多考点标签，如果盲目地按照一个标签内部所有习题的顺序去刷题，会让人有点错乱感。对于时间比较紧凑的同学来说，题目的数量比较多，想在较短时间内刷完是一个很大的挑战。因此，本文针对时间较紧凑的同学精选一些数组类型的代表性题目，进行分类总结，希望能够起到一点帮助（PS：其实是作者希望借此进一步加深自己对考点的认知，建立一个有效的知识体系… …）。

标记为数组类型的题目有200多道题，本文的重点关注那些主要考察数组的题目。对于考察点主要放在其它考点（比如：二分查找、双指针、哈希表等）上的题目，作者计划把这些题目放在后序总结篇章中。按照作者刷题的情况，在属于数组考点系列的题目中，划分为四个常考问题：子数组问题、矩阵问题、O(n)类型问题和思维转换类型问题。

• 子数组问题：就是给定一个数组，围绕该数组的子数组列出诸多难题，等待我们来解答。
• 矩阵问题：给定一个矩阵（或者称为二维数组），围绕该矩阵列出不同方式遍历矩阵中元素等难题，等待我们来解答。
• O(n)类型问题：O(n)是指时间复杂度为O(n)，给定的题目题意一般很容易理解，其一般解法（俗称暴力解法，时间复杂度一般为O(n^2)，甚至更高）也很简单，但是题目要求你的解法时间复杂度为O(n)。看到这些题目的某些解答后，会让我们忍不住夸赞：真乃神人、好厉害、奇异特解、巧妙、强、优雅。
• 思维转换类型问题：其解答不属于上述三种类型问题，但是解答方式有点巧妙，或者说该类型题目较为基础，很可能考察你的快速应用代码能力的题目。（PS: 其实是作者自己也不好划分，但是认为有点价值的题目… …）

本文是《LeetCode刷题总结-数组篇（上）》，总结归纳有关子数组问题的题目。本期题目数量共17题，其中难度为简单有1题，难度为中等的有12题，难度为困难的有4题。具体题目信息及解答见下文。

例1 最大子序和

题号：53，难度：简单

题目描述：

解题思路：

本题最为经典和广泛的解法是应用动态规划的思想来解答，其时间复杂度为O(n)。题目中鼓励尝试使用更为精妙的分治法求解，通过翻阅相关解答和评论发现，分治法并没有动态规划解答的优雅，其时间复杂度为O(nlogn)，也并不是最优。所以，介绍一下应用动态规划解题的思路。

从数组第一个元素开始遍历，用一个一维数组存储遍历到当前元素的最大连续子数组的和。

当遍历到第i个元素时，如果前i-1和元素中连续子数组和加上第i个元素时比第i个元素的值要大，那么就更新dp[i] = dp[i-1] + nums[i]，否则dp[i] = nums[i]。

具体代码：

class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length + 1];
        int result = nums[0];
        for(int i = 0;i < nums.length;i++) {
            dp[i+1] = Math.max(dp[i]+nums[i], nums[i]);
            result = Math.max(dp[i+1], result);
        }
 
        return result;
    }
}

执行结果：

例2 乘积最大子序列

题号：152，难度：中等

题目描述：

解题思路：

这题其实是例1 最大子序和一个变例，由加法变换成了乘法操作（依旧是应用动态规划的思路）。此时需要做的改变是定义两个变量来存储当前子序列的乘积，一个是保存最大值，一个是保存最小值（包含负数的子序列）。

具体代码：

class Solution {
    public int maxProduct(int[] nums) {
        int result = nums[0], n_max = 1, n_min = 1;
        for(Integer n: nums) {
            if(n < 0) {
                int temp = n_max;
                n_max = Math.max(n_min * n, n);
                n_min = Math.min(temp * n, n);
            } else {
                n_max = Math.max(n_max * n, n);
                n_min = Math.min(n_min * n, n);
            }
 
            result = Math.max(n_max, result);
        }
 
        return result;
    }
}

执行结果：

例3 子集

题号：78，难度：中等。（可参考子集II, 题号90，难度：中等）

题目描述：

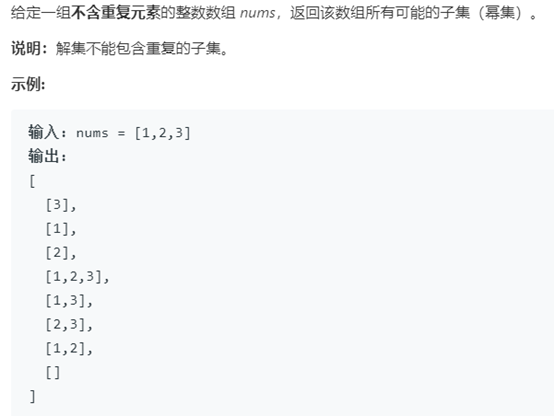
解题思路：

本题考查我们应用回溯来求解所有子集的问题，在一些算法教材中最经典的问题时求解全排列的问题，解法和这道题类似。

此题需要特别注意的是，首先采用链表在递归过程中添加元素，在回溯时删除元素，能够有效提高时间效率。其次，给递归调用程序设计一个start参数，可以避免同一个元素被重复递归调用，达到了剪枝效果。

最后，在结果列表中采用重新创建一个列表存储子集的结果，是因为在递归函数中列表参数只对应一个地址，采用重新创建相当于应用了深拷贝的思想，避免了结果均为空集的情况。

具体代码：

class Solution {
    private List<List<Integer>> result;
 
    public List<List<Integer>> subsets(int[] nums) {
        result = new ArrayList<>();
        if(nums.length <= 0)
            return result;
        dfs(nums, 0, new LinkedList<Integer>());
 
        return result;
    }
 
    public void dfs(int[] nums, int start, LinkedList<Integer> list) {
        result.add(new ArrayList<Integer>(list));
        for(int i = start;i < nums.length;i++) {
            list.addLast(nums[i]);
            dfs(nums, i + 1, list);
            list.removeLast();
        }
    }
}

执行结果：

例4 最长连续序列

题号：128，难度：困难

题目描述：

解题思路：

采用哈希表存储数组中所有元素，然后应用哈希表查询当前元素的左右两边序列数字是否存在，查询操作的时间复杂度为O(1)，所以整体的时间复杂度为O(n)。

具体代码：

class Solution {
    public int longestConsecutive(int[] nums) {
        int result = 0;
        Set<Integer> set = new HashSet<>();
        for(Integer n: nums)
            set.add(n);
        for(Integer n: nums) {
            if(set.contains(n)) {
                int len = 1;
                int temp = n;
                while(set.contains(--temp)) {
                    len++;
                    set.remove(temp);
                }
                temp = n;
                while(set.contains(++temp)) {
                    len++;
                    set.remove(temp);
                }
                result = Math.max(result, len);
            }
        }
 
        return result;
    }
}

执行结果：

例5 乘积小于K的子数组

题号：713，难度：中等

题目描述：

解题思路：

本题考查应用双指针的思想，一前一后同时往后遍历。

具体代码：

class Solution {
    public int numSubarrayProductLessThanK(int[] nums, int k) {
        int result = 0, left = 0, right = 0;
        int target = 1;
        while(right < nums.length) {
            target *= nums[right++];
            while(left < right && target >= k)
                target = target / nums[left++];
            result += (right - left);
        }
 
        return result;
    }
}

执行结果:

例6 和为K的子数组

题号：560，难度：中等

题目描述：

解题思路：

本题采用哈希表存储从数组第一个元素不断往后的子序列和，然后判断到当前元素的序列总和减去K的值在哈希表中有多少个，即为包含当前元素的子序列可以得到目标结果，利用前后子序列的差可以得到目标子序列和为K。

具体代码：

class Solution {
    public int subarraySum(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0, 1);
        int sum = 0, result = 0;
 
        for(int i = 0; i < nums.length; ++i) {
            sum += nums[i];
            if(map.containsKey(sum-k))
                result += map.get(sum-k);
            map.put(sum, map.getOrDefault(sum, 0)+1);
        }
 
        return result;
    }
}

执行结果：

例7 可被K整除的子数组

题号：974，难度：中等

题目描述：

解题思路：

从第一个元素开始，求取连续子数组的余数（sum % k），采用Map存储每个余数的个数。

相同余数的子数组个数大于等于2时，任意选取其中两个子数组余数相减，即余数抵消，可得到一个符合题目要求的sum。（此处的个数计算方式为：n*(n-1) / 2）

但是，此处有两个需要注意的点:

(1) 如果余数为0，最终0的余数个数只有一个时（1*（1-1）/2 = 0），这样计算会漏掉（如果为多个，也会有遗漏，可以自己计算，可以自己稍微琢磨）。所以，在初始化Map时，添加以下代码：

map.put(0, 1); 

(2) 如果余数为负数，就不能执行相同余数相减抵消的操作。此时，需要做以下处理：

// sum % K 正常计算方法
 
((sum % K) + K) % K   // 如果为负数时，需要转换为正数，这个转换原

具体代码：

class Solution {
    public int subarraysDivByK(int[] A, int K) {
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0, 1);
        int result = 0;
        int sum = 0;
 
        for(Integer a: A) {
            sum += a;
            map.put(((sum % K) + K) % K , map.getOrDefault(((sum % K) + K) % K, 0)+1);
        }
        // System.out.println("map = "+map);
        for(Integer key: map.keySet())
            result += map.get(key) * (map.get(key) - 1) / 2;
 
        return result;
    }
}

执行结果：

例8 三个无重叠子数组的最大和

题号：689，难度：困难

题目描述：

解题思路：

采用动态规划求解，状态转移方程：dp[2][n] = max(dp[2][n-1], dp[1][n-k] + sumRange(n, n -k+1))。其中一维长度为3，表示三个子数组。

具体代码（代码引用自LeetCode的一个题解）：

class Solution {
     public int[] maxSumOfThreeSubarrays(int[] nums, int k) {
        int[][] dp = new int[3][nums.length];
        int[] cummulative = new int[nums.length];
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            cummulative[i] = sum;
        }
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < nums.length; j++) {
                if (j < (i + 1) * k - 1) {
                    dp[i][j] = 0;
                } else {
                    if (i == 0) {
                        // 易错点: 当k=1的时候，边界条件需要处理一下。
                        dp[i][j] = Math.max(j > 0 ? dp[i][j - 1] : 0, rangeSum(cummulative, j - k + 1, j));
                    } else {
                        dp[i][j] = Math.max(j > 0 ? dp[i][j - 1]: 0, rangeSum(cummulative, j - k + 1, j) + dp[i - 1][j - k]);
                    }
                }
 
            }
        }
        int[] ans = new int[3];
        int length = dp[2].length - 1;
        for (int i = 2; i >= 0; i--) {
            int[] row = dp[i];
            for (int j = length - 1; j >= 0; j--) {
                if (row[j] != row[length]) {
                    ans[i] = j - k + 2;
                    length = j - k + 1;
                    break;
                }
            }
        }
        return ans;
    }
 
    private int rangeSum(int[] cummulative, int left, int right) {
        if (left == 0) {
            return cummulative[right];
        } else {
            return cummulative[right] - cummulative[left - 1];
        }
    }
 
}

执行结果：

例9 最长重复子数组

题号：718，难度：中等

题目描述：

解题思路：

本题既可以用哈希表来解答，也可以用动态规划的思想来解答。应用动态规划的思路解答的时间效率最高。此处介绍一下动态规划的解题思路。dp[i][j]表示A [i-1]为终点,B[j-1]为终点时两者的最长公共子数组。具体更新策略见代码。

具体代码：

class Solution {
      public int findLength(int[] A, int[] B) {
 
        int[][] dp = new int[A.length + 1][B.length + 1];
        int res = 0;
        for (int i = 1; i <= A.length; i++)
            for (int j = 1; j <= B.length; j++) {
 
                if (A[i - 1] == B[j - 1])
                    dp[i][j] = dp[i - 1][j - 1] + 1;
 
                res = Math.max(res, dp[i][j]);
            }
 
        return res;
    }
}

执行结果：

例10 匹配子序列的单词数

题号：792，难度：中等

题目描述：

解题思路：

要特别注意子序列的含义，子序列是按照从前往后的顺序任意多个元素组成的序列，其中的顺序不能更改。因此，不能应用哈希表统计字母的个数来判断是否包含某个单词。此处可采用暴力法直接匹配查找，时间效率较低。此处可采用二分查找来优化匹配结果，能提高时间效率。

具体代码（贴一个LeetCode上评论的代码）：

class Solution {
    List<Integer> index[]=new ArrayList[26];
 
    public int numMatchingSubseq(String S, String[] words) {
         for(int i=0;i<S.length();i++){
            char ch=S.charAt(i);
            if(index[ch-'a']==null)
                index[ch-'a']=new ArrayList();
            index[ch-'a'].add(i);
         }
         int res=0,pre;
         for(String str:words){
            pre=-1;
            for(int i=0;i<str.length();i++){
                pre=helper(str.charAt(i)-'a',pre);
                if(pre==-1)
                    break;
            }
            if(pre!=-1)
                res++;
         }
         return res;
    }
 
    private int helper(int i,int pre){
        if(index[i]==null)
            return -1;
 
        int l=0,r=index[i].size()-1;
        if(pre==-1)
            return index[i].get(0);
        if(index[i].get(r)<=pre)
            return -1;
 
        while(l<r){
            int mid=(l+r)/2;
            if(index[i].get(mid)<=pre)
                l=mid+1;
            else
                r=mid;
        }
 
        return index[i].get(l);
   }
}

执行结果：

例11 区间子数组个数

题号：795， 难度：中等

题目描述：

解题思路：

最大元素满足大于等于L小于等于R的子数组个数 = 最大元素小于等于R的子数组个数 - 最大元素小于L的子数组个数。

具体代码：

class Solution {
    public int numSubarrayBoundedMax(int[] A, int L, int R) {
        return numSubarrayBoundedMax(A, R) - numSubarrayBoundedMax(A, L - 1);
    }
 
    private int numSubarrayBoundedMax(int[] A, int Max) {
        int res = 0;
        int numSubarry = 0;
        for (int num : A) {
            if (num <= Max) {
                numSubarry++;
                res += numSubarry;
            } else {
                numSubarry = 0;
            }
        }
        return res;
    }
}

执行结果：

例12 子数组的最小值之和

题号：907，难度：中等

题目描述：

解题思路：

参考自LeetCode的评论解答：计算每个数在子数组中最小的次数。

具体代码：

class Solution {
    public int sumSubarrayMins(int[] A) {
        long res = 0;
        long mod = 1000000007;
        for (int i = 0; i<A.length; i++) {
            int l = i-1;
            for (; l>=0 && A[i] < A[l]; l--) ;
            int r = i+1;
            for (; r<A.length && A[i] <= A[r]; r++) ;
 
            res += (i-l)*(r-i)*A[i];
        }
        return (int)(res % mod);
    }
}

执行结果：

例13 子序列宽度之和

题号：891，难度：困难

题目描述：

解题思路：

具体可参考LeetCode的一篇题解。

具体代码：

class Solution {
    public int sumSubseqWidths(int[] A) {
        final int MOD = (int) (1e9 + 7);
        Arrays.sort(A);
        int n = A.length;
        long res = 0;
        long p = 1;
        for (int i = 0; i < n; ++i) {
            res = (res + (A[i] - A[n - 1 - i]) * p) % MOD;
            p = (p << 1) % MOD;
        }
        return (int) ((res + MOD) % MOD);
    }
}

执行结果：

例14 环形子数组的最大和

题号：918， 难度：中等

题目描述：

解题思路：

因为题目要求有环形，所以需要定义两个变量。一个变量存储当前无环形是的连续最大子数组和，一个存储无环形连续最小子数组和。最后采用数组的总和减去最小和，和已经保存的最大和进行比较。另外，需要注意一点如果数组全部为负数时，此时直接返回子数组的最大值（因为此时，最小子数组和就是数组的和）。

具体代码：

class Solution {
    public int maxSubarraySumCircular(int[] A) {
        int max = A[0];
        int min = A[0];
        int maxSoFar = A[0];
        int minSoFar = A[0];
        int sum = A[0];
        for (int i=1;i<A.length;i++) {
          sum += A[i];
          maxSoFar = Math.max(A[i],maxSoFar+A[i]);
          minSoFar = Math.min(A[i],minSoFar+A[i]);
          max = Math.max(max,maxSoFar);
          min = Math.min(min,minSoFar);
        }
        if (max < 0)
            return max;
        return Math.max(max,sum-min);
    }
}

执行结果:

例15 最长湍流子数组

题号：978，难度：中等

题目描述：

解题思路：

采用连续三个位置数据是否符合湍流特征来判断，时间复杂度为O(n)。

具体代码(引用自LeetCode一个评论代码)：

class Solution {
    public int maxTurbulenceSize(int[] A) {
        int N = A.length;
        int ans = 1;
        int anchor = 0;
 
        for (int i = 1; i < N; ++i) {
            int c = Integer.compare(A[i-1], A[i]);
            if (i == N-1 || c * Integer.compare(A[i], A[i+1]) != -1) {
                if (c != 0) ans = Math.max(ans, i - anchor + 1);
                anchor = i;
            }
        }
 
        return ans;
    }
}

执行结果：

例16 两个非重叠子数组的最大和

题号：1031，难度：中等

题目描述：

解题思路：

采用滑动窗口的思路来解答，对长度为L的数组，采用大小为L的滑动窗口，对于长度为M的数组采用大小为M的窗口。然后，通过两个窗口之间的距离来遍历。

具体代码：

class Solution {
    public  int maxSumTwoNoOverlap(int[] A, int L, int M) {
        int len = A.length, dpL[] = new int[len - L + 1], dpM[] = new int[len - M + 1], max = 0;
        for (int i = 0; i < L; i++)
            dpL[0] += A[i];
        for (int i = 0; i < M; i++)
            dpM[0] += A[i];
        for (int i = 1; i < len - L + 1; i++)
            dpL[i] = dpL[i - 1] + A[i + L - 1] - A[i - 1];
        for (int i = 1; i < len - M + 1; i++)
            dpM[i] = dpM[i - 1] + A[i + M - 1] - A[i - 1];
        for (int i = 0; i < len - L - M + 1; i++) {
            int count = len - i - L - M;
            while (count >= 0) {
                max = Math.max(max, Math.max(dpL[i] + dpM[i + L + count], dpM[i] + dpL[i + M + count]));
                count--;
            }
        }
        return max;
    }
}

执行结果：

例17 子数组中占绝大多数的元素

题号：1157，难度：困难

题目描述：

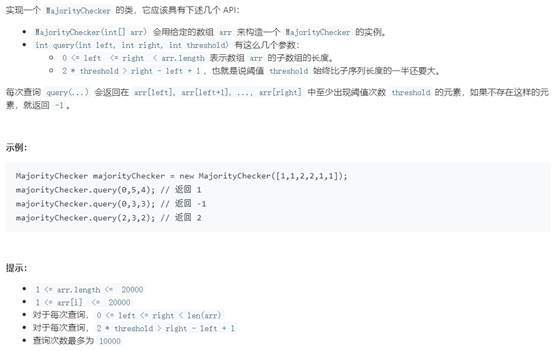
解题思路：

采用哈希数组来解答，一旦哈希数组中目标元素值大于等于threshold，就返回目标数字，否则返回-1。

具体代码：

class MajorityChecker {
 
    private int[] nums;
    private int[] ans;
    private int max;
 
    public MajorityChecker(int[] arr) {
        nums = arr;
        max = arr[0];
        for(int x : arr)
            if(x > max)
                max = x;
 
    }
 
    public int query(int left, int right, int threshold) {
        ans = new int[max + 5];
        for(int i = left;i <= right;i++){
            if(++ans[nums[i]] >= threshold)
                return nums[i];
        }
        return -1;
    }
}

执行结果：