Admiral（双向BFS + Hash）

Problem Description

Suppose that you are an admiral of a famous naval troop. Our naval forces have got 21 battleships. There are 6 types of battleships. First, we have got one flagship in which the admiral must be and it is denoted by number 0. Others are denoted by number from 1 to 5, each of them has 2, 3, 4, 5, 6 ships of its kind. So, we have got 21 battleships in total and we must take a giant battle against the enemy. Hence, the correct strategy of how to arrange each type of battleships is very important to us. The shape of the battlefield is like the picture that is shown below. 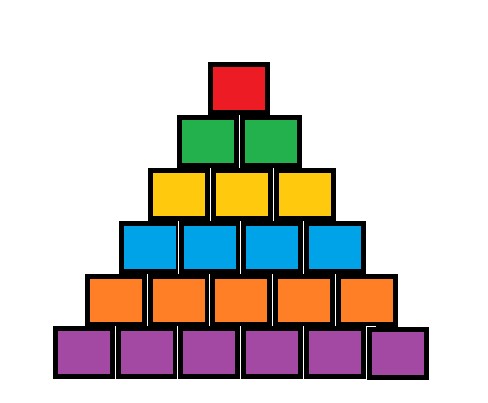To simplify the problem, we consider all battleships have the same rectangular shape.Fortunately, we have already known the optimal state of battleships. As you can see, the battlefield consists of 6 rows. And we have 6 types of battleship, so the optimal state is that all the battleships denoted by number i are located at the i-th row. Hence, each type of battleship corresponds to different color. You are given the initial state of battlefield as input. You can change the state of battlefield by changing the position of flagship with adjacent battleship. Two battleships are considered adjacent if and only if they are not in the same row and share parts of their edges. For example, if we denote the cell which is at i-th row and j-th position from the left as (i,j), then the cell (2,1) is adjacent to the cells (1,0), (1,1), (3,1), (3,2). Your task is to change the position of the battleships minimum times so as to reach the optimal state. Note: All the coordinates are 0-base indexed.

Input

The first line of input contains an integer T (1 <= T <= 10), the number of test cases.  Each test case consists of 6 lines. The i-th line of each test case contains i integers, denoting the type of battleships at i-th row of battlefield, from left to right.

Output

For each test case, if you can’t reach the goal in no more than 20 moves, you must output “too difficult” in one line. Otherwise, you must output the answer in one line.

SampleInput

1
1
2 0
2 1 2
3 3 3 3
4 4 4 4 4
5 5 5 5 5 5

SampleOutput

3

题意就是给你一个6*6的塔，上下两个相邻的单位可以进行交换，问最少进行几次交换，可以得到
0
1 1
2 2 2
3 3 3 3
……………………
这种状态，开始思路是用A*做，结果A*不是很熟练，没搞出来，写了个直接搜索炸了，然后我也是看了一下网上博客，使用双向搜索就行了。
思路就是从末尾开始往前搜索10步，从开始状态往后搜索10步，分别状态压缩一下存在map中，然后就看有没有两种相同的状态，否则就输出太难了。
代码：

 #include <bits/stdc++.h>
 using namespace std;
 #define ll long long
 int fx[][] = {,,,,-,-,-,};    //左下，右下，左上，右上

 struct node{
     ll p[][];
     int r,c;
     int flag;
     int step;

     node(){}
     node(int _r,int _c,int _flag,int _step):r(_r),c(_c),flag(_flag),step(_step){}
 };

 queue<node>q;
 map<ll,ll>p[];　　//分别存储两个方向的bfs状态

 ll _hash(node a){　　//用hash压缩路径状态
     ll res = ;
     for(int i = ; i < ; i++){
         for(int j = ; j <= i; j++){
             res = res* + a.p[i][j];
         }
     }
     return res;
 }

 int bfs(node &s,node &e){
     while(!q.empty()){
         q.pop();
     }
     p[].clear();
     p[].clear();
     q.push(s);
     q.push(e);
     p[s.flag][_hash(s)] = ;　　//必须要标记一下，因为后面会用到count函数查询是否存在
     p[e.flag][_hash(e)] = ;
     while(!q.empty()){
         node now = q.front();
         q.pop();
         ll sta = _hash(now);
         if(p[!now.flag].count(sta)){
             int num = p[!now.flag][sta] +  now.step;
             if(num <= )
                 return num;
             else
                 continue;
         }

         if(now.step >= )　　//处理10步即可
             continue;
         for(int i = ; i < ; i++){
             node nxt = now;
             nxt.step++;
             nxt.r += fx[i][];
             nxt.c += fx[i][];
             if(nxt.r <  || nxt.r >  || nxt.c <  || nxt.c > nxt.r)
                 continue;
             swap(nxt.p[now.r][now.c],nxt.p[nxt.r][nxt.c]);
             if(p[nxt.flag].count(_hash(nxt)) == )
                 p[nxt.flag][_hash(nxt)] = nxt.step;
             q.push(nxt);
         }
     }
     return -;
 }

 int main(){
     int t;
     cin>>t;
     node s, e;
     while(t--){
         for(int i = ; i < ; i++){
             for(int j = ; j <= i; j++){
                 cin>>s.p[i][j];
                 if(s.p[i][j] == )
                     s.r = i, s.c = j;
                 e.p[i][j] = i;
             }
         }
         s.flag = ;
         s.step = ;
         e = node(,,,);
         int ans = bfs(s,e);
         if(ans >=  && ans <= )
             cout << ans << endl;
         else
             cout << "too difficult" << endl;
     }
     return ;
 }