什么是 B 树?
本文提到的「B-树」,就是「B树」,都是 B-tree 的翻译,里面不是减号-,是连接符-。因为有人把 B-tree 翻成 「B-树」,让人以为「B树」和「B-树」是两种树,实际上两者就是同一种树。
Mysql数据库里面的索引是基于什么数据结构了呢?
主要是基于Hash表或者B+树。
B+树的具体实现细节?B-树和B+树有什么区别呢?联合索引在B+树中如何存储呢?
要知道这些,我们需要先了解什么是B-树。数据库索引之所以要使用树结构存储,是因为树的查询效率高,而且可以保持有序。为什么索引不使用二叉查找来树来实现呢?(///二叉查找树查询的时间复杂读是0(logN),性能已经足够高了啊,难道B树可以比它更快?)其实从算法逻辑上讲,二叉查找树的查找速度和比较次数都是最小的,但是为我们不得不考虑一个现实的问题:磁盘 IO。
数据库索引是存储在磁盘上的,当数据量比较打的时候,索引的大小可能有几个G甚至更多。当我们利用索引查询的时候,能把整个索引全部加载到内存吗?不可能,能做的只有逐一的加载每一个磁盘页对应着索引树的节点。

如果我们利用二叉查找树作为索引结构,情形是什么呢?假设树的高度是4,查找的值是10,流程如下:
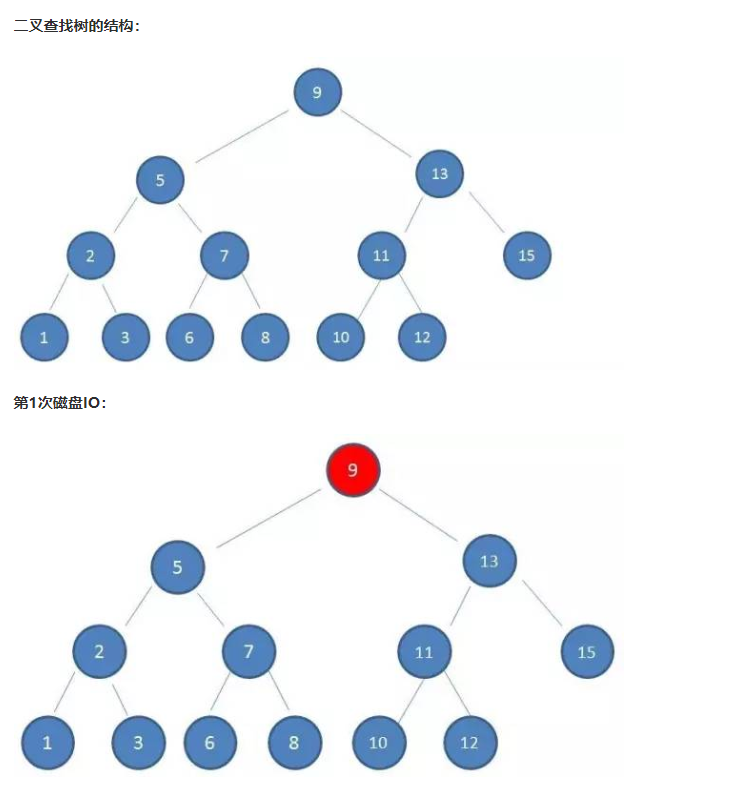


由上可以看出,磁盘IO的次数是由索引树高度决定,所以为了减少磁盘IO次数,我们需要减少树的高度,这就是B-树的特征之一。
B树的定义:
两种定义:用阶定义的B树 & 用阶定义的B树
用阶定义的B树 :
B 树又叫平衡多路查找树。一棵m阶的B 树 (注:切勿简单的认为一棵m阶的B树是m叉树,虽然存在四叉树,八叉树,KD树,及vp/R树/R*树/R+树/X树/M树/线段树/希尔伯特R树/优先R树等空间划分树,但与B树完全不等同)的特性如下:
- 树中每个结点最多含有m个孩子(m>=2);
- 除根结点和叶子结点外,其它每个结点至少有[ceil(m / 2)]个孩子(其中ceil(x)是一个取上限的函数);
- 若根结点不是叶子结点,则至少有2个孩子(特殊情况:没有孩子的根结点,即根结点为叶子结点,整棵树只有一个根节点);
- 所有叶子结点都出现在同一层,叶子结点不包含任何关键字信息(其实,关键是把什么当做叶子结点,因为如红黑树中,每一个NULL指针即当做叶子结点,只是没画出来而已)。
- 每个非终端结点中包含有n个关键字信息: (n,P0,K1,P1,K2,P2,......,Kn,Pn)。其中:
a) Ki (i=1...n)为关键字,且关键字按顺序升序排序K(i-1)< Ki。
b) Pi为指向子树根的接点,且指针P(i-1)指向子树种所有结点的关键字均小于Ki,但都大于K(i-1)。
c) 关键字的个数n必须满足: [ceil(m / 2)-1]<= n <= m-1。如下图所示:

用度定义的B树:
针对上面的5点,再阐述下:B树中每一个结点能包含的关键字(如之前上面的D H和Q T X)数有一个上界和下界。这个下界可以用一个称作B树的最小度数(算法导论中文版上译作度数,最小度数即内节点中节点最小孩子数目)m(m>=2)表示。
每个非根的内结点至多有m个子女,每个非根的结点必须至少含有m-1个关键字,如果树是非空的,则根结点至少包含一个关键字;
每个结点可包含至多2m-1个关键字。所以一个内结点至多可有2m个子女。如果一个结点恰好有2m-1个关键字,我们就说这个结点是满的(而稍后介绍的B*树作为B树的一种常用变形,B*树中要求每个内结点至少为2/3满,而不是像这里的B树所要求的至少半满);
当关键字数m=2(t=2的意思是,mmin=2,m可以>=2)时的B树是最简单的(有很多人会因此误认为B树就是二叉查找树,但二叉查找树就是二叉查找树,B树就是B树,B树是一棵含有m(m>=2)个关键字的平衡多路查找树),此时,每个内结点可能因此而含有2个、3个或4个子女,亦即一棵2-3-4树,然而在实际中,通常采用大得多的t值。
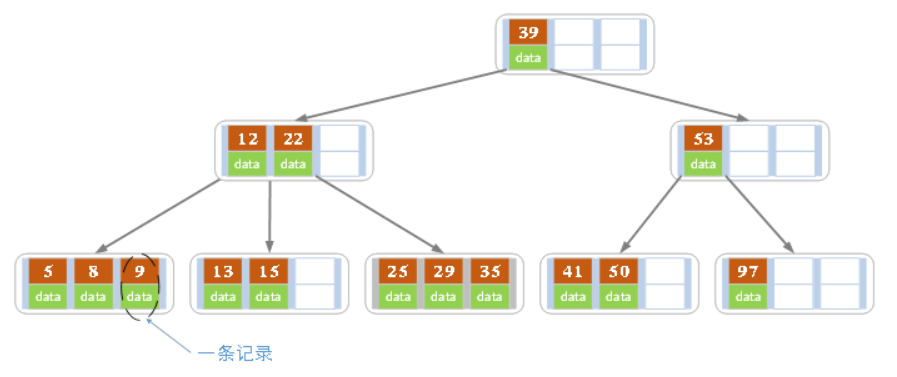
上图是一颗阶数为4的B树。在实际应用中的B树的阶数m都非常大(通常大于100),所以即使存储大量的数据,B树的高度仍然比较小。每个结点中存储了关键字(key)和关键字对应的数据(data),以及孩子结点的指针。我们将一个key和其对应的data称为一个记录。
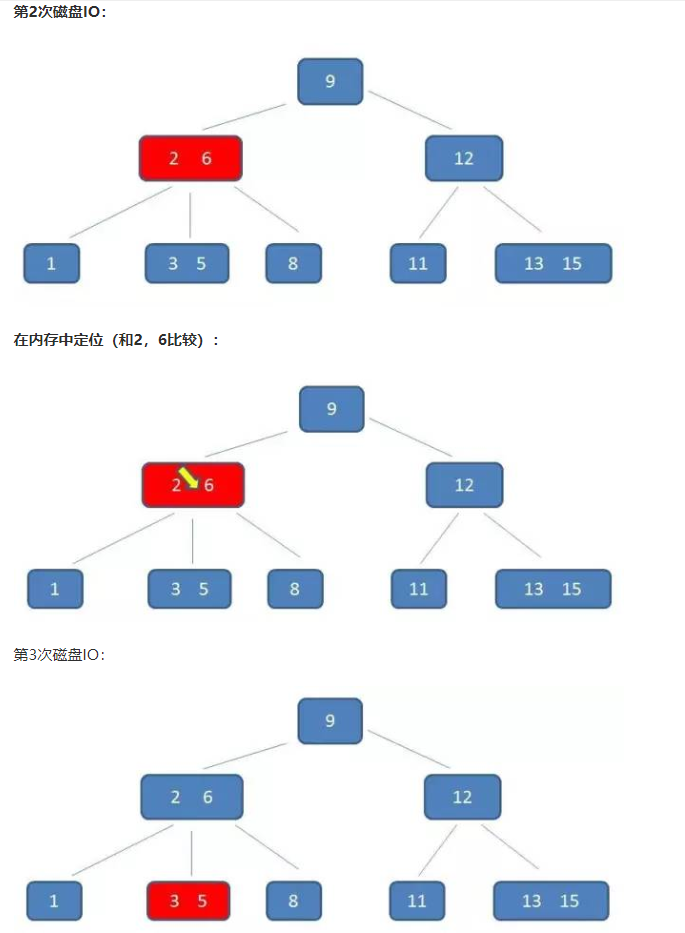
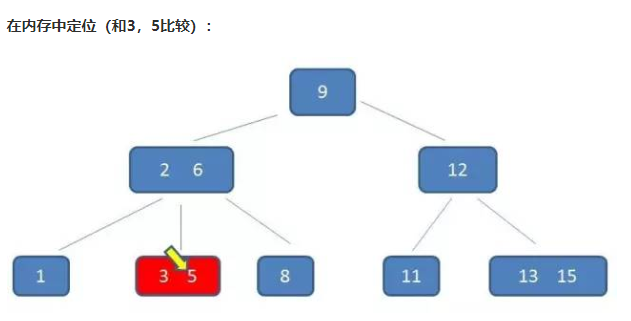
B-树的查询:
演示如下:假设查询5


插入:
B-树的插入过程比较复杂,我们只举一个最金典的例子,插入4

删除:11
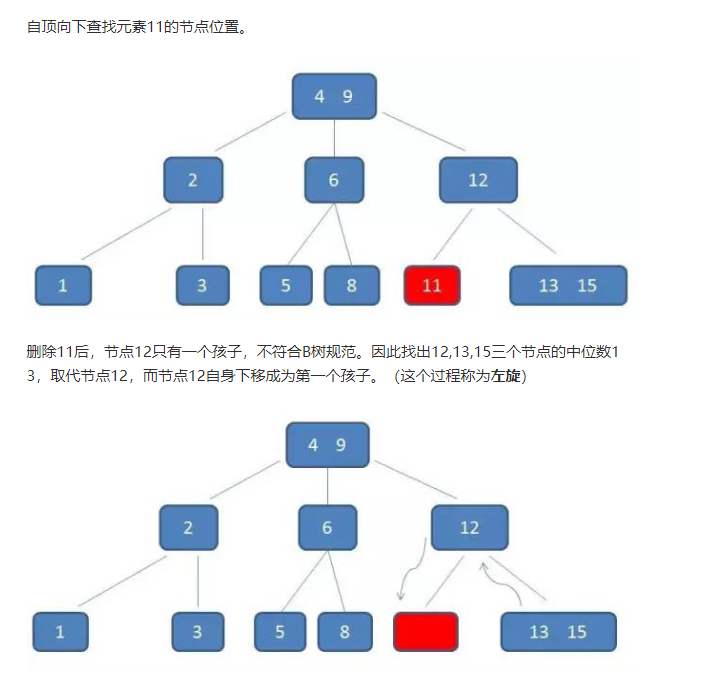
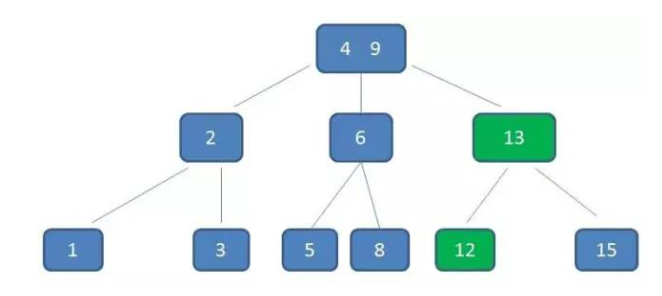
什么是 B 树?的更多相关文章
- B树——算法导论(25)
B树 1. 简介 在之前我们学习了红黑树,今天再学习一种树--B树.它与红黑树有许多类似的地方,比如都是平衡搜索树,但它们在功能和结构上却有较大的差别. 从功能上看,B树是为磁盘或其他存储设备设计的, ...
- ASP.NET Aries 入门开发教程8:树型列表及自定义右键菜单
前言: 前面几篇重点都在讲普通列表的相关操作. 本篇主要讲树型列表的操作. 框架在设计时,已经把树型列表和普通列表全面统一了操作,用法几乎是一致的. 下面介绍一些差距化的内容: 1:树型列表绑定: v ...
- 再讲IQueryable<T>,揭开表达式树的神秘面纱
接上篇<先说IEnumerable,我们每天用的foreach你真的懂它吗?> 最近园子里定制自己的orm那是一个风生水起,感觉不整个自己的orm都不好意思继续混博客园了(开个玩笑).那么 ...
- HDU1671——前缀树的一点感触
题目http://acm.hdu.edu.cn/showproblem.php?pid=1671 题目本身不难,一棵前缀树OK,但是前两次提交都没有成功. 第一次Memory Limit Exceed ...
- 算法与数据结构(十一) 平衡二叉树(AVL树)
今天的博客是在上一篇博客的基础上进行的延伸.上一篇博客我们主要聊了二叉排序树,详情请戳<二叉排序树的查找.插入与删除>.本篇博客我们就在二叉排序树的基础上来聊聊平衡二叉树,也叫AVL树,A ...
- [C#] C# 知识回顾 - 表达式树 Expression Trees
C# 知识回顾 - 表达式树 Expression Trees 目录 简介 Lambda 表达式创建表达式树 API 创建表达式树 解析表达式树 表达式树的永久性 编译表达式树 执行表达式树 修改表达 ...
- bzoj3207--Hash+主席树
题目大意: 给定一个n个数的序列和m个询问(n,m<=100000)和k,每个询问包含k+2个数字:l,r,b[1],b[2]...b[k],要求输出b[1]~b[k]在[l,r]中是否出现. ...
- bzoj1901--树状数组套主席树
树状数组套主席树模板题... 题目大意: 给定一个含有n个数的序列a[1],a[2],a[3]--a[n],程序必须回答这样的询问:对于给定的i,j,k,在a[i],a[i+1],a[i+2]--a[ ...
- bzoj3932--可持久化线段树
题目大意: 最近实验室正在为其管理的超级计算机编制一套任务管理系统,而你被安排完成其中的查询部分.超级计算机中的 任务用三元组(Si,Ei,Pi)描述,(Si,Ei,Pi)表示任务从第Si秒开始,在第 ...
- jquery-treegrid树状表格的使用(.Net平台)
上一篇介绍了DataTable,这一篇在DT的基础之上再使用jquery的一款插件:treegrid,官网地址:http://maxazan.github.io/jquery-treegrid/ 一. ...
随机推荐
- 小米平板2 win10 MIUI互刷教程
在这篇文章中,我们会为大家提供Windows 10版小米平板2刷入MIUI和MIUI版小米平板2刷入Windows 10的两组教程. 不过从Win 10刷MIUI需要用原生安卓系统过渡来统一bios版 ...
- 支持向量机(SVM)举例
例(1) 无核(No kernel or linear kernel) 代码和数据集来自于https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes ...
- python selenium简单安装及使用
1.安装 pip install selenium 2.下载浏览器对应的Driver 链接地址:https://sites.google.com/a/chromium.org/chromedriver ...
- 剑指Offer_编程题_19
题目描述 输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2, ...
- Hbase CMS GC 调优。
export HBASE_OPTS="-XX:+UseConcMarkSweepGC" export HBASE_LOG_DIR=/app/hbase/logexport HBAS ...
- 1.3浅谈Spring(IOC容器的实现)
这一节我们来讨论IOC容器到底做了什么. 还是借用之前的那段代码 ClassPathXmlApplicationContext app = new ClassPathXmlApplicationCon ...
- CMDB资产管理系统开发【day25】:windows客户端开发
1.目录结构 PS Y:\MadkingClient> tree /f 卷 netgame 的文件夹 PATH 列表 卷序列号为 ACE3-896E Y:. ├─bin │ NedStark.p ...
- MVCC 能解决幻读吗?
MySQL通过MVCC(解决读写并发问题)和间隙锁(解决写写并发问题)来解决幻读 MySQL InnoDB事务的隔离级别有四级,默认是“可重复读”(REPEATABLE READ). 未提交读(REA ...
- [物理学与PDEs]第5章习题4 广义 Hookean 定律的张量的对称性
设材料是超弹性的, 并设参考构形为自然状态, 证明由线性化得到的张量 ${\bf A}=(a_{ijkl})=\sex{2\cfrac{\p \bar p_{ij}}{c_{kl}}}$ 具有以下的对 ...
- bzoj2733 永无乡 splay树的启发式合并
https://vjudge.net/problem/HYSBZ-2733 给一些带权点,有些点是互相连通的, 然后给出2种操作,在两点间加一条边,或者询问一个点所在的连通块内的第k小值的编号 并查集 ...
