机器学习 - 正则化L1 L2

L1 L2 Regularization

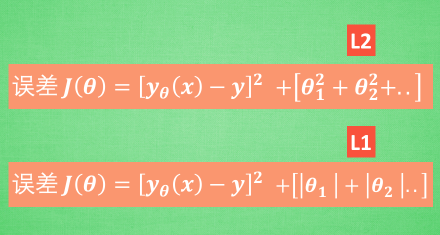
表示方式：

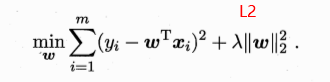
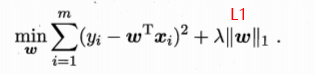
$L_2\text{ regularization term} = ||\boldsymbol w||_2^2 = {w_1^2 + w_2^2 + ... + w_n^2}$

执行 L₂ 正则化对模型具有以下影响

• 使权重值接近于 0（但并非正好为 0）
• 使权重的平均值接近于 0，且呈正态（钟形曲线或高斯曲线）分布。

模型开发者通过以下方式来调整正则化项的整体影响：用正则化项的值乘以名为 lambda（又称为正则化率）的标量。也就是说，模型开发者会执行以下运算：

$\text{minimize(Loss(Data|Model)} + \lambda \text{ complexity(Model))}$

增加 lambda 值将增强正则化效果。 例如，lambda 值较高的权重直方图可能会如图 2 所示。

降低 lambda 的值往往会得出比较平缓的直方图，如图 3 所示。

参考：

https://developers.google.com/machine-learning/crash-course/regularization-for-simplicity/lambda?hl=zh-cn

https://zhuanlan.zhihu.com/p/25707761