2019南昌邀请赛网络预选赛 J.Distance on the tree（树链剖分）

传送门

题意：

　　给出一棵树，每条边都有权值；

　　给出 m 次询问，每次询问有三个参数 u,v,w ，求节点 u 与节点 v 之间权值 ≤ w 的路径个数；

题解：

　　昨天再打比赛的时候，中途，凯少和我说，这道题，一眼看去，就是树链剖分，然鹅，太久没写树链剖分的我一时也木有思路；

　　今天上午把树链剖分温习了一遍，做了个模板题；

　　下午再想了一下这道题，思路喷涌而出............

　　首先，介绍一下相关变量：

 int fa[maxn];//fa[u]:u的父节点
 int son[maxn];//son[u]:u的重儿子
 int dep[maxn];//dep[u]:u的深度
 int siz[maxn];//siz[u]:以u为根的子树节点个数
 int tid[maxn];//tid[u]:u在线段树中的位置
 int top[maxn];//top[u]:u所在重链的祖先节点
 int e[maxn][];//e[i][0]与e[i][1]有条权值为e[i][2]的边
 vector<int >v[maxn<<];//v[i]:存储线段树中i号节点的所有边的权值

　　（树链剖分，默认来看这篇博客的都会辽，逃）　　

　　下面重点介绍一下v[]的作用（将样例2中的权值改为了10）：

　　

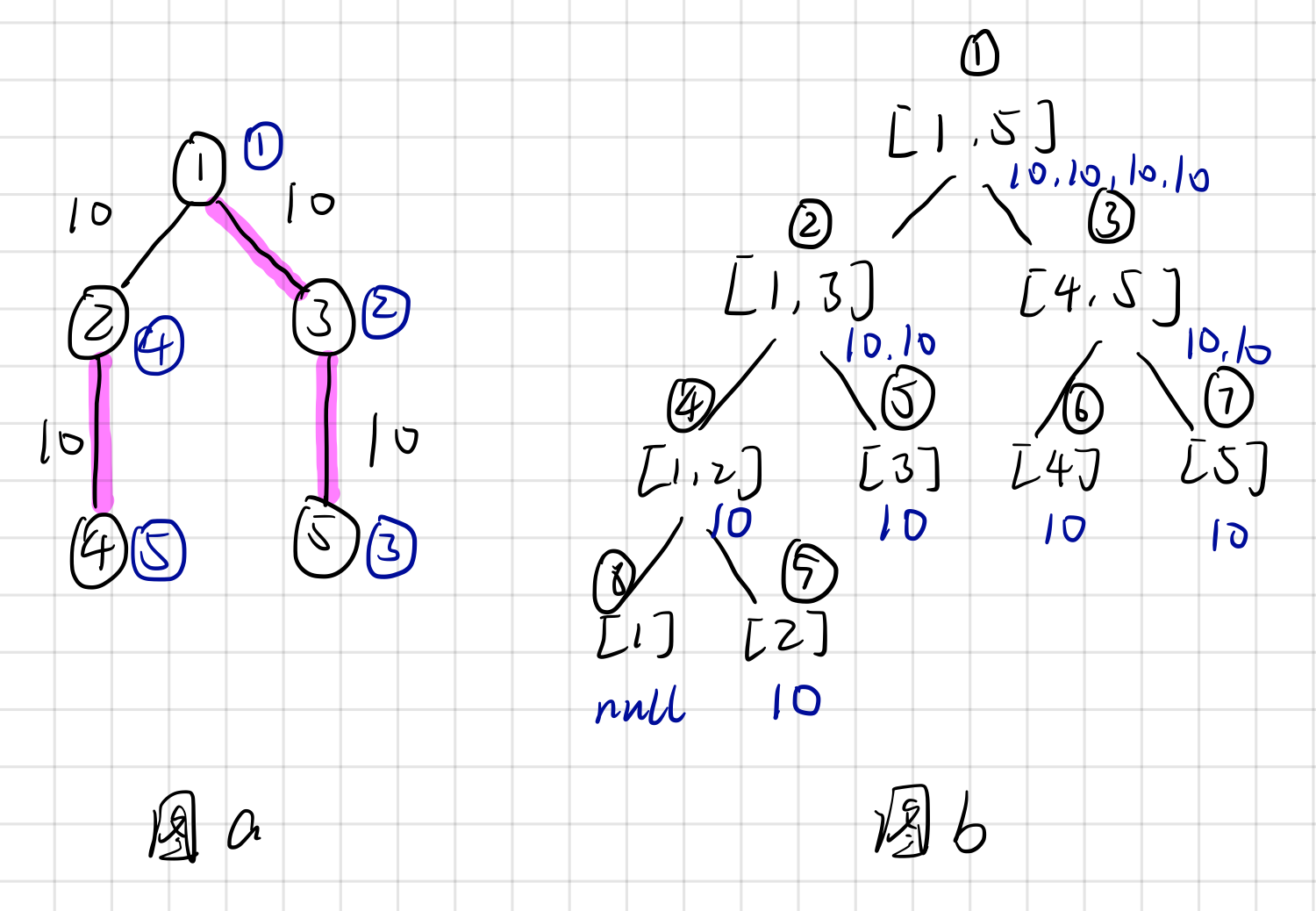
　　由树链剖分可知（图a，紫色部分代表重链）

　　　　tid[1]=1,tid[3]=2,tid[5]=3;

　　　　tid[2]=4,tid[4]=5;

　　那么，线段树维护啥呢？

 struct SegmentTree
 {
     int l,r;
     int mid()
     {
         return l+((r-l)>>);
     }
 }segTree[maxn<<];
 vector<int >v[maxn<<];//v[i]:存储线段树中i号节点的所有边的权值

　　对于我而言，此次线段树，主要维护节点 i 的左右区间[l,r]，重点是 v[] 中维护的东西；

　　首先将边权存到线段树中，如何存呢？

　　对于边 u,v,w ，（假设 fa[v]=u），将 w 存在 v[ tid[ v ] ]中；

　　看一下Update()函数：

 //将节点x在线段树中对应的pos位置的v中加入val
 void Update(int x,int val,int pos)
 {
     if(segTree[pos].l == segTree[pos].r)
     {
         v[pos].push_back(val);//val加入到v[pos]中
         return ;
     }
     int mid=segTree[pos].mid();
     if(x <= mid)
         Update(x,val,ls(pos));
     else
         Update(x,val,rs(pos));
 }

　　例如上图b：

　　①-② : 10 ,调用函数Update(tid[2],10,1) ⇔ v[tid[2]].push_back(10)

　　①-③ : 10 ,调用函数Update(tid[3],10,1) ⇔ v[tid[3]].push_back(10)

　　②-④ : 10 ,调用函数Update(tid[4],10,1) ⇔ v[tid[4]].push_back(10)

　　③-⑤ : 10 ,调用函数Update(tid[5],10,1) ⇔ v[tid[5]].push_back(10)

　　线段树中的节点9中的v存储一个10

　　线段树中的节点5中的v存储一个10

　　线段树中的节点6中的v存储一个10

　　线段树中的节点7中的v存储一个10

　　这个就是Update()函数的作用；

　　接下来的pushUp()函数很重要：

 void pushUp(int pos)
 {
     if(segTree[pos].l == segTree[pos].r)
         return;
 
     pushUp(ls(pos));
     pushUp(rs(pos));
 
     //将ls(pos),rs(pos)中的元素存储到pos中
     for(int i=;i < v[ls(pos)].size();++i)
         v[pos].push_back(v[ls(pos)][i]);
     for(int i=;i < v[rs(pos)].size();++i)
         v[pos].push_back(v[rs(pos)][i]);
     sort(v[pos].begin(),v[pos].end());//升序排列
 }

　　调用pushUp(1)，将所有的pos 的 ls(pos),rs(pos) 节点信息更新到pos节点；

　　调用完这个函数后，你会发现：

　　v[1]:10,10,10,10（[1,5]中的所有节点到其父节点的权值，根节点为null）

　　v[2]:10,10（[1,3]中的所有节点到其父节点的权值）

　　v[3]:10,10（[4,5]中的所有节点到其父节点的权值）

　　v[4]:10（[1,2]中的所有节点到其父节点的权值）

　　v[5]:10（[3,3]中的所有节点到其父节点的权值）

　　v[6]:10（[4,4]中的所有节点到其父节点的权值）

　　v[7]:10（[5,5]中的所有节点到其父节点的权值）

　　v[8]:null（根节点为null）

　　v[9]:10（[2,2]中的所有节点到其父节点的权值）

　　你会发现，v[i]中存的值就是[ tree[i].l , tree[i].r ]中所有节点与其父节点的权值；

　　接下来就是询问操作了：

 int BS(int pos,int w)
 {
     int l=-,r=v[pos].size();
     while(r-l > )
     {
         int mid=l+((r-l)>>);
         if(v[pos][mid] <= w)
             l=mid;
         else
             r=mid;
     }
     return l+;
 }
 int Query(int l,int r,int pos,int w)
 {
     if(v[pos][] > w)//当前区间的如果最小的值要 > w，直接返回0
         return ;
     if(segTree[pos].l == l && segTree[pos].r == r)
         return BS(pos,w);//二分查找pos区间值 <= w 得个数（还记得pushUp()中的sort函数么？
 
     int mid=segTree[pos].mid();
     if(r <= mid)
         return Query(l,r,ls(pos),w);
     else if(l > mid)
         return Query(l,r,rs(pos),w);
     else
         return Query(l,mid,ls(pos),w)+Query(mid+,r,rs(pos),w);
 }

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 #define ls(x) (x<<1)
 #define rs(x) (x<<1|1)
 #define INF 0x3f3f3f3f
 #define mem(a,b) memset(a,b,sizeof(a))
 const int maxn=1e5+;
 
 int n,m;
 int fa[maxn];//fa[u]:u的父节点
 int son[maxn];//son[u]:u的重儿子
 int dep[maxn];//dep[u]:u的深度
 int siz[maxn];//siz[u]:以u为根的子树节点个数
 int tid[maxn];//tid[u]:u在线段树中的位置
 int top[maxn];//top[u]:u所在重链的祖先节点
 int e[maxn][];//e[i][0]与e[i][1]有条权值为e[i][2]的边
 vector<int >v[maxn<<];//v[i]:存储线段树中i号节点的所有边的权值
 int num;
 int head[maxn];
 struct Edge
 {
     int to;
     int w;
     int next;
 }G[maxn<<];
 void addEdge(int u,int v,int w)
 {
     G[num].to=v;
     G[num].w=w;
     G[num].next=head[u];
     head[u]=num++;
 }
 struct SegmentTree
 {
     int l,r;
     int mid()
     {
         return l+((r-l)>>);
     }
 }segTree[maxn<<];
 void DFS1(int u,int f,int depth)
 {
     fa[u]=f;
     son[u]=-;
     siz[u]=;
     dep[u]=depth;
     for(int i=head[u];~i;i=G[i].next)
     {
         int v=G[i].to;
         if(v == f)
             continue;
         DFS1(v,u,depth+);
 
         siz[u] += siz[v];
 
         if(son[u] == - || siz[v] > siz[son[u]])
             son[u]=v;
     }
 }
 void DFS2(int u,int anc,int &k)
 {
     top[u]=anc;
     tid[u]=++k;
     if(son[u] == -)
         return ;
     DFS2(son[u],anc,k);
 
     for(int i=head[u];~i;i=G[i].next)
     {
         int v=G[i].to;
         if(v != fa[u] && v != son[u])
             DFS2(v,v,k);
     }
 }
 void pushUp(int pos)
 {
     if(segTree[pos].l == segTree[pos].r)
         return;
 
     pushUp(ls(pos));
     pushUp(rs(pos));
 
     //将ls(pos),rs(pos)中的元素存储到pos中
     for(int i=;i < v[ls(pos)].size();++i)
         v[pos].push_back(v[ls(pos)][i]);
     for(int i=;i < v[rs(pos)].size();++i)
         v[pos].push_back(v[rs(pos)][i]);
     sort(v[pos].begin(),v[pos].end());//升序排列
 }
 void buildSegTree(int l,int r,int pos)
 {
     segTree[pos].l=l;
     segTree[pos].r=r;
     if(l == r)
         return ;
 
     int mid=l+((r-l)>>);
     buildSegTree(l,mid,ls(pos));
     buildSegTree(mid+,r,rs(pos));
 }
 //将节点x在线段树中对应的pos位置的v中加入val
 void Update(int x,int val,int pos)
 {
     if(segTree[pos].l == segTree[pos].r)
     {
         v[pos].push_back(val);//val加入到v[pos]中
         return ;
     }
     int mid=segTree[pos].mid();
     if(x <= mid)
         Update(x,val,ls(pos));
     else
         Update(x,val,rs(pos));
 }
 int BS(int pos,int w)
 {
     int l=-,r=v[pos].size();
     while(r-l > )
     {
         int mid=l+((r-l)>>);
         if(v[pos][mid] <= w)
             l=mid;
         else
             r=mid;
     }
     return l+;
 }
 int Query(int l,int r,int pos,int w)
 {
     if(v[pos][] > w)//当前区间的如果最小的值要 > w，直接返回0
         return ;
     if(segTree[pos].l == l && segTree[pos].r == r)
         return BS(pos,w);//二分查找pos区间值 <= w 得个数（还记得pushUp()中的sort函数么？
 
     int mid=segTree[pos].mid();
     if(r <= mid)
         return Query(l,r,ls(pos),w);
     else if(l > mid)
         return Query(l,r,rs(pos),w);
     else
         return Query(l,mid,ls(pos),w)+Query(mid+,r,rs(pos),w);
 }
 int Find(int u,int v,int w)//查询节点u到节点v之间权值小于等于w得路径个数
 {
     int ans=;
     int topU=top[u];
     int topV=top[v];
     while(topU != topV)
     {
         if(dep[topU] > dep[topV])
         {
             swap(u,v);
             swap(topU,topV);
         }
         ans += Query(tid[top[v]],tid[v],,w);
         v=fa[topV];
         topV=top[v];
     }
     if(u == v)
         return ans;
     if(dep[u] > dep[v])
         swap(u,v);
     return ans+Query(tid[son[u]],tid[v],,w);
 }
 void Solve()
 {
     DFS1(,,);
     int k=;
     DFS2(,,k);
 
     buildSegTree(,k,);
 
     for(int i=;i < n;++i)
     {
         if(dep[e[i][]] > dep[e[i][]])
             swap(e[i][],e[i][]);//令fa[e[i][1]] = e[i][0]，方便更新操作
         Update(tid[e[i][]],e[i][],);//将e[i][2]加入到tid[e[i][1]]中
     }
     pushUp();//更新线段树中所有的pos
 
     for(int i=;i <= m;++i)
     {
         int u,v,w;
         scanf("%d%d%d",&u,&v,&w);
         printf("%d\n",Find(u,v,w));
     }
 }
 void Init()
 {
     num=;
     mem(head,-);
     for(int i=;i < *maxn;++i)
         v[i].clear();
 }
 int main()
 {
 //    freopen("C:\\Users\\hyacinthLJP\\Desktop\\in&&out\\contest","r",stdin);
     while(~scanf("%d%d",&n,&m))
     {
         Init();
         for(int i=;i < n;++i)
         {
             scanf("%d%d%d",e[i]+,e[i]+,e[i]+);
             addEdge(e[i][],e[i][],e[i][]);
             addEdge(e[i][],e[i][],e[i][]);
         }
         Solve();
     }
     return ;
 }