[FJOI2018]领导集团问题

dp[i][j]，i为根子树，最上面的值是j，选择的最大值

观察dp方程

1.整体Dp已经可以做了。

2.考虑优美一些的做法：

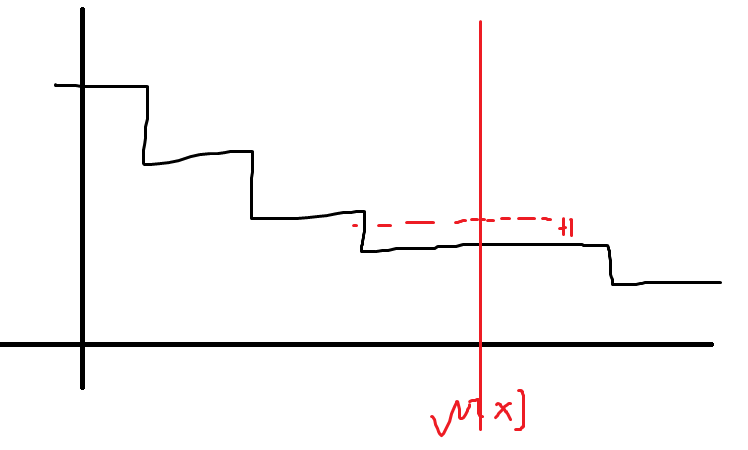
dp[i]如果对j取后缀最大值，显然是不上升的分段函数

而段数就是子树sz

树形Dp的时候，子树之间可以直接把分段函数按位相加。对于<=w[x]的，可以额外获得从dp[i][w[x]]+1得到的转移

1.用map维护，启发式合并，但是合并整体加上一些数不能维护具体值，所以维护差分值！

2.额外转移，找到前驱p，p+1到w[x]整体+1，差分数组上，就是dp[x][w[x]]++,dp[x][p]--

任何时候，如果键值变成0，必须删除。否则第二问就错了。

分段函数、整体Dp都是基于整体上值域个数有限进行的trick

整体Dp运用线段树合并，还可以支持打标记，适用面其实更广。

[九省联考2018]秘密袭击coat

分段函数，通常处理后缀最值，由于单调，通过记录差分数组可以O(1)进行区间加减，启发式合并。如果涉及区间函数平移操作，表现更为灵活。

模拟赛 yjqb

[FJOI2018]领导集团问题的更多相关文章

  1. [FJOI2018]领导集团问题 mulitset合并

    P4577 [FJOI2018]领导集团问题 链接 luogu bzoj 他是个重题 bzoj4919: [Lydsy1706月赛]大根堆 代码改改就过了 思路 求树上的lis,要好好读题目的!!! ...

  2. 【BZOJ5469】[FJOI2018]领导集团问题（动态规划，线段树合并）

    [BZOJ5469][FJOI2018]领导集团问题(动态规划,线段树合并) 题面 BZOJ 洛谷 题解 题目就是让你在树上找一个最大的点集,使得两个点如果存在祖先关系,那么就要满足祖先的权值要小于等 ...

  3. P4577 [FJOI2018]领导集团问题

    P4577 [FJOI2018]领导集团问题 我们对整棵树进行dfs遍历,并用一个multiset维护对于每个点,它的子树可取的最大点集. 我们遍历到点$u$时: 不选点$u$,显然答案就为它的所有子 ...

  4. 5469: [FJOI2018]领导集团问题

    5469: [FJOI2018]领导集团问题 链接 题意: 要求在一棵树内选一个子集,满足子集内的任意两个点u,v,如果u是v的祖先,那么u的权值小于等于v. 分析: dp[u][i]表示在u的子树内 ...

  5. 题解-FJOI2018 领导集团问题

    题面 FJOI2018 领导集团问题 给一棵树 \(T(|T|=n)\),每个点有个权值 \(w_i\),从中选出一个子点集 \(P=\{x\in {\rm node}|x\in T\}\),使得 \ ...

  6. 「题解报告」P4577 [FJOI2018]领导集团问题

    题解 P4577 [FJOI2018]领导集团问题 题解区好像没有线段树上又套了二分的做法,于是就有了这片题解. 题目传送门 怀着必 WA 的决心交了两发,一不小心就过了. 题意 求一个树上最长不下降 ...

  7. 洛谷P4577 [FJOI2018]领导集团问题(dp 线段树合并)

    题意 题目链接 Sol 首先不难想到一个dp,设\(f[i][j]\)表示\(i\)的子树内选择的最小值至少为\(j\)的最大个数 转移的时候维护一个后缀\(mx\)然后直接加 因为后缀max是单调不 ...

  8. 洛谷4577 & LOJ2521：[FJOI2018]领导集团问题——题解

    https://www.luogu.org/problemnew/show/P4577 https://loj.ac/problem/2521 参考:https://www.luogu.org/blo ...

  9. bzoj5469 [FJOI2018]领导集团问题

    题目描述: bz luogu 题解: 相当于树上$LIS$问题. 考虑一维情况下的贪心,我们可以用multiset启发式合并搞. 代码: #include<set> #include< ...

随机推荐

  1. Unity协程的坑

    unity终止协程提供了  StopAllCoroutines() 和 StopCoroutines() 两个方法, 但是都只能终止该文件内的 IEnumerator. 并且具体使用有点坑, 见如下实 ...

  2. Linux中ftp的常用命令

    转自:https://www.jb51.net/article/103904.htm FTP命令 ftp> ascii # 设定以ASCII方式传送文件(缺省值) ftp> bell # ...

  3. 常用SMTP地址

    1.QQ邮箱(mail.qq.com) POP3服务器地址:pop.qq.com(端口:110) SMTP服务器地址:smtp.qq.com(端口:25) 2.搜狐邮箱(sohu.com): POP3 ...

  4. 定时任务 Cron表达式

    Cron表达式由6~7项组成,中间用空格分开.从左到右依次是: 秒.分.时.日.月.周几.年(可省略) Cron表达式的值可以是数字,也可以是以下符号: "*":所有值都匹配 &q ...

  5. python之单元测试_生成测试报告

    (1)HTMLTestRunner.py的下载路径:https://pan.baidu.com/s/1Yk2E8d8bIo5_rmpussOE9Q 提取码:0jae (2)HTMLTestRunner ...

  6. Scrapy案例01-爬取传智播客主页上的老师信息

    目录 1. 新建scrapy项目 2. 爬虫文件: 2.1. 查看需要爬取内容存在哪里: 2.2. 设置item需要保存的数据变量 2.3. 创建爬虫文件 2.4. 保存数据 2.5. yield的用 ...

  7. JavaScript Uncaught TypeError: Cannot read property 'value' of null

    用 JavaScript 操作 DOM 时出现如下错误: Uncaught TypeError: Cannot set property 'value' of null Uncaught TypeEr ...

  8. Spring系列-SpringBoot 学习路径

    学习spring boot 已经有很长一段时间,与其说学习,不如说是使用. 在过去的很长时间我一直奉行实用主义,任何技术我都是在应用中使用,很少是因为为了学习而学习. 当然,有那么几次心血来潮,去专门 ...

  9. Python爬虫 爬取百合网的女人们和男人们

    学Python也有段时间了,目前学到了Python的类.个人感觉Python的类不应称之为类,而应称之为数据类型,只是数据类型而已!只是数据类型而已!只是数据类型而已!重要的事情说三篇. 据书上说一个 ...

  10. Codeforces Global Round 2 Solution

    这场题目设置有点问题啊,难度:Div.2 A->Div.2 B->Div.2 D->Div.2 C->Div.2 D->Div.1 D-> Div.1 E-> ...