Tinghua Data Mining 7

SVM

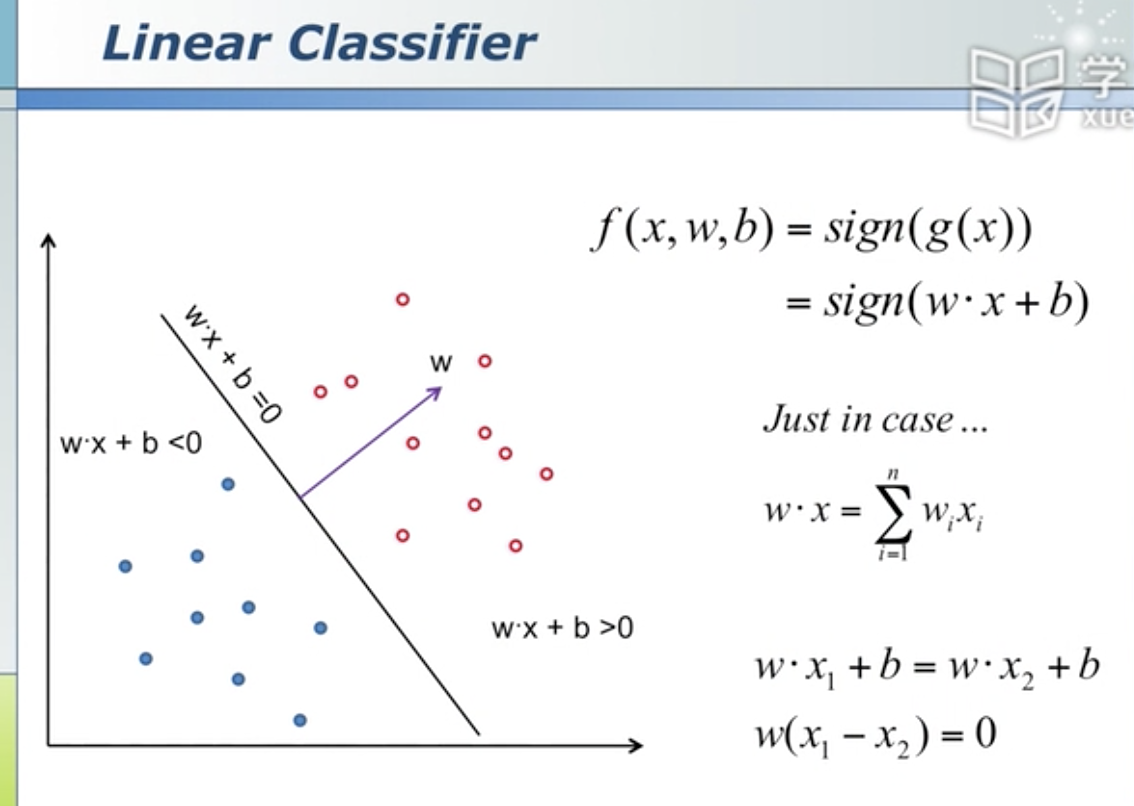
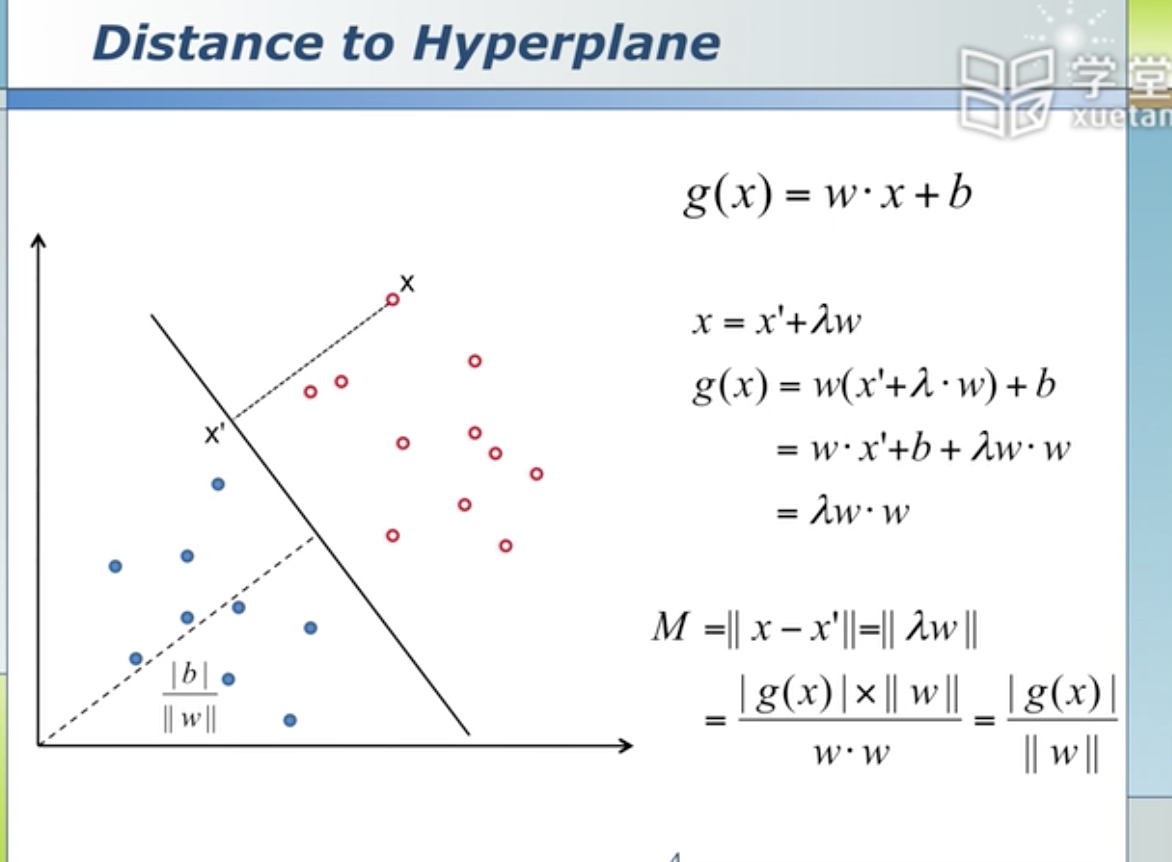
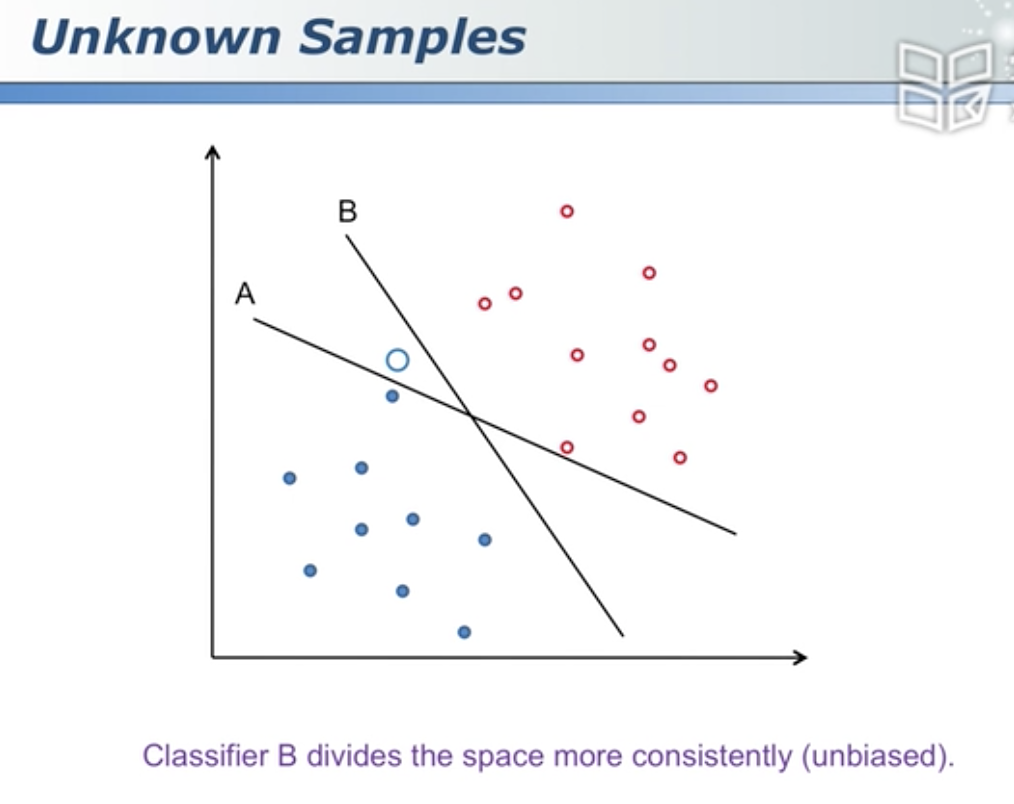
B分割得更加无偏 比较公平

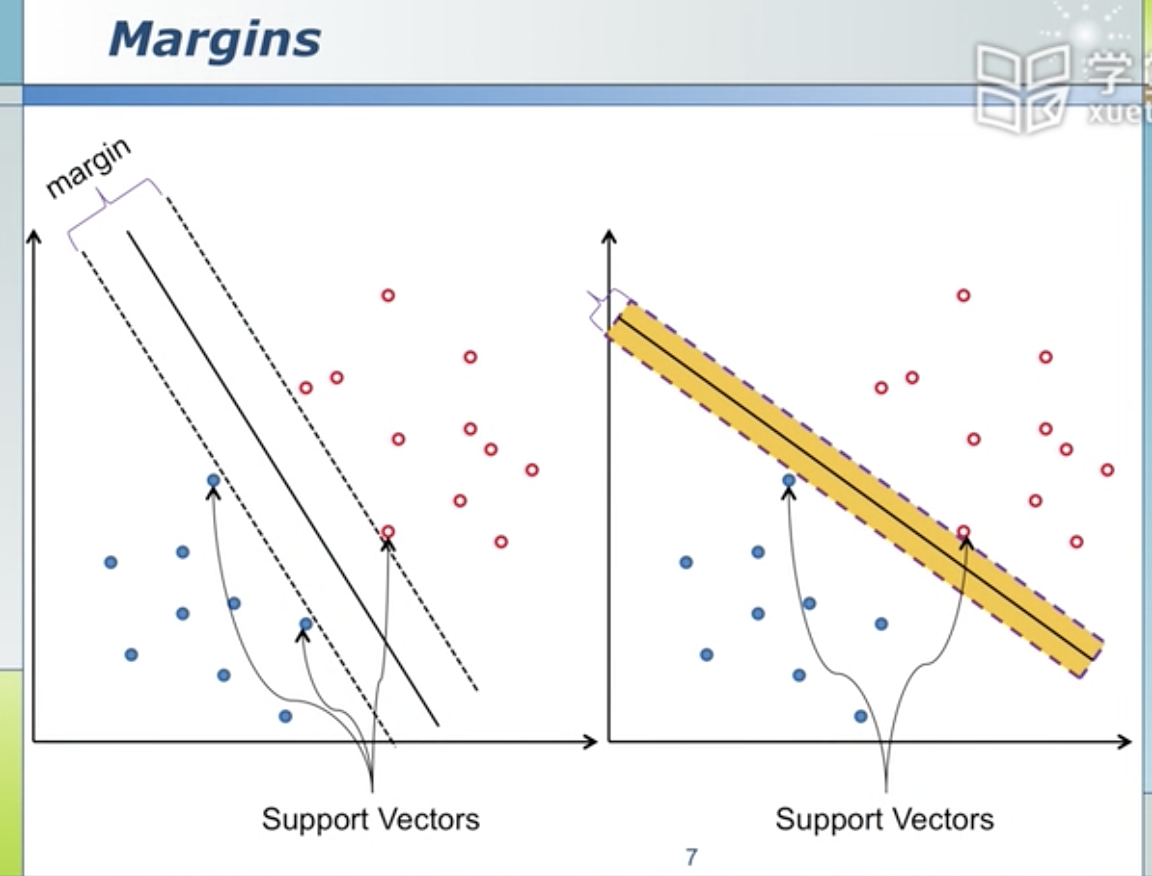
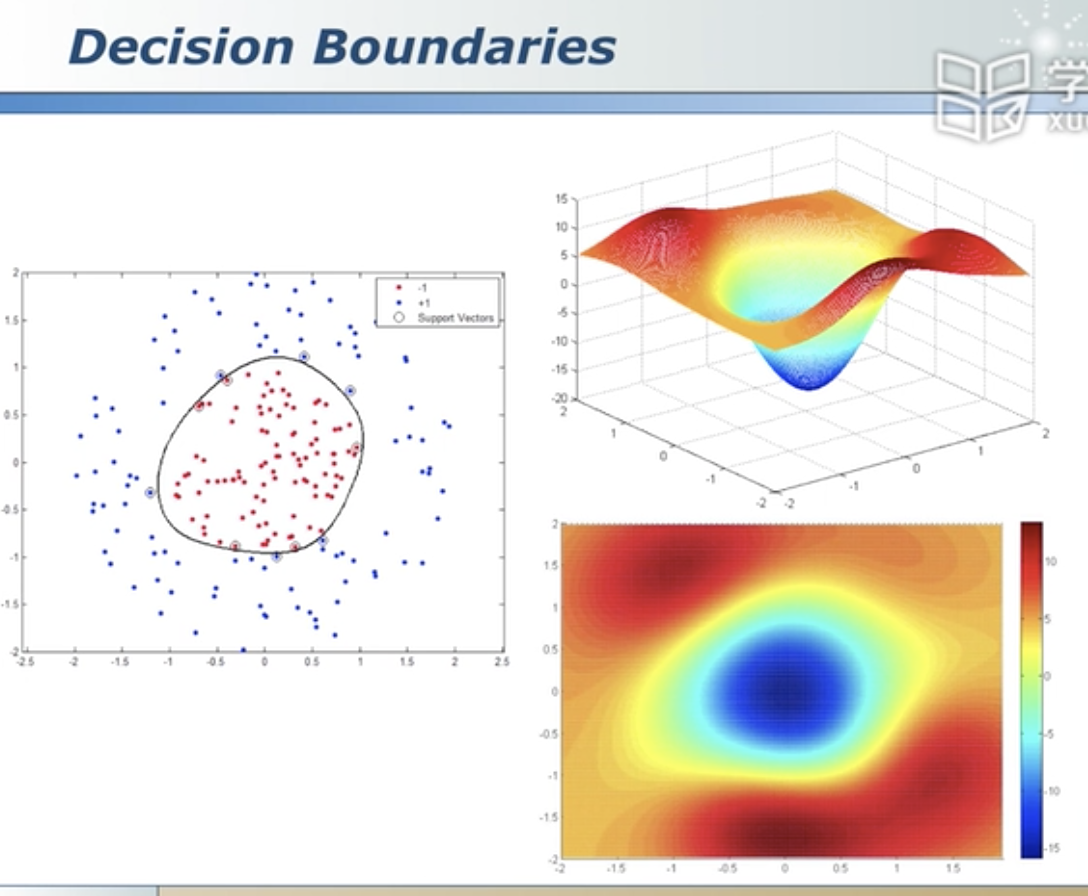
卡着分界面的点叫支持向量，就好比托着分界面 支持向量决定了可移动的范围，这个范围就叫margin 分界面可移动的距离

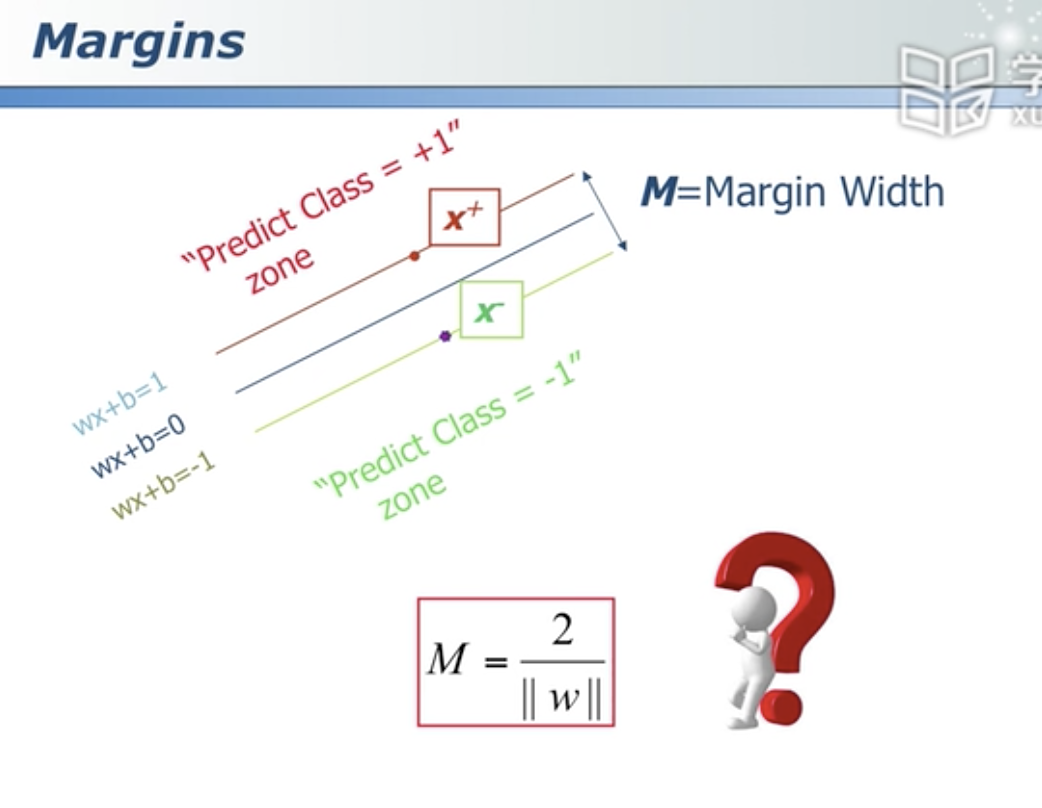
前提是先要被分对

对偶问题一般是不等价的，但是在SVM这里，在满足一些条件的前提下，是等价的。对偶之后，只有alpha，没有w和b

很多alpha是等于0的，只有少数的alpha是不等于0的，非0的乘起来 支持向量

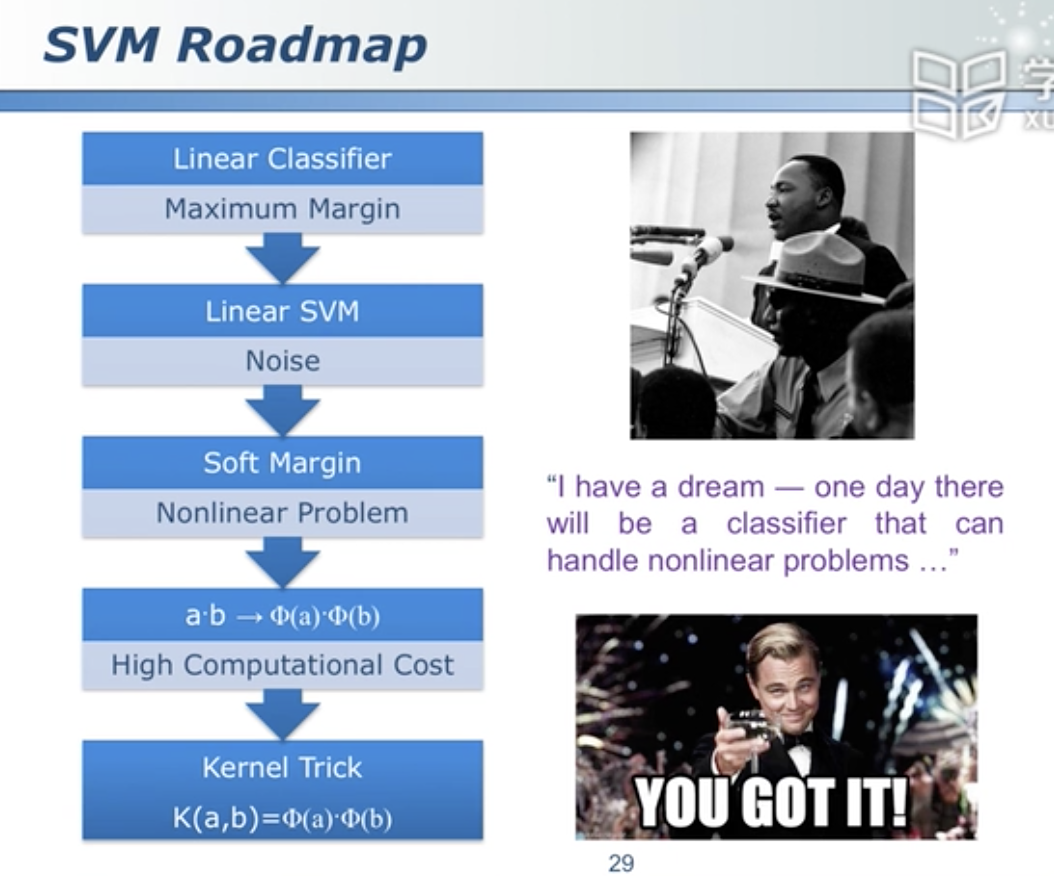
放宽了约束条件，比如学生学的太差，60分及格的话有人过不了，于是说加上10分之后能够有60分就可以了。
既然放宽了，在目标函数中就要有所体现，要加上一个惩罚量。

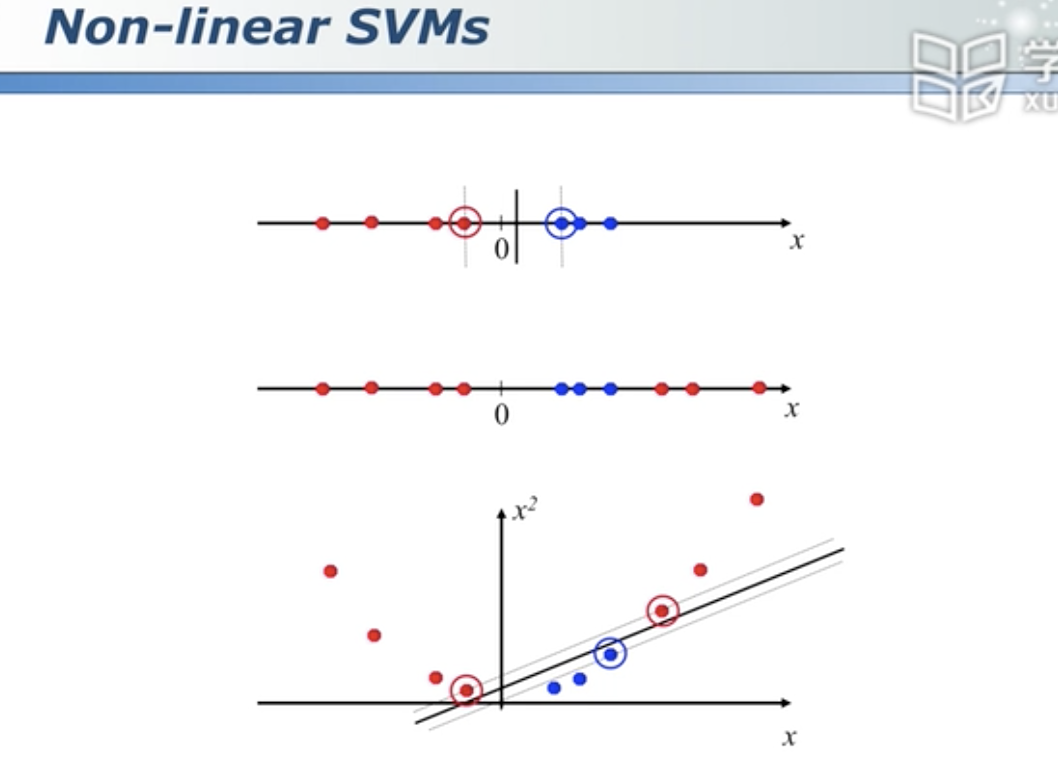
映射不是唯一的。

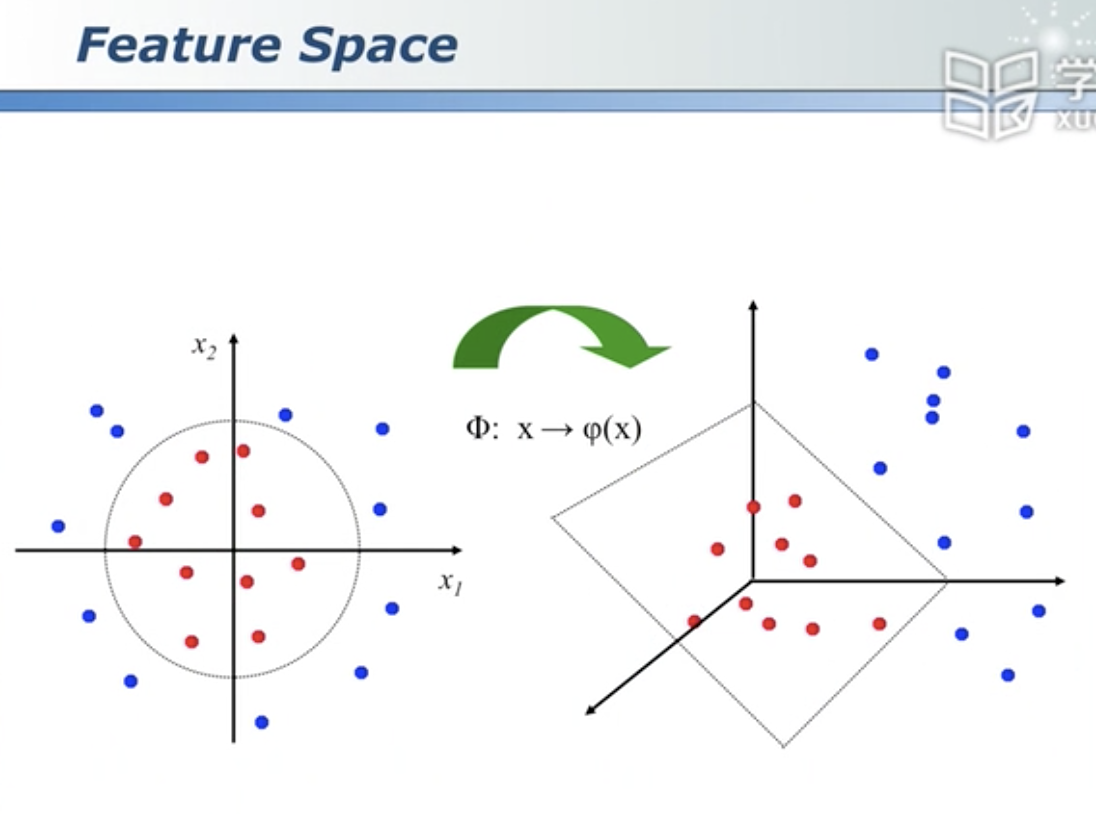
不用去设计映射，因为高维空间的数据长什么样子你也不知道，它都是使用集中固定的映射方法。这是其中一种。

向量作内积

既发挥了高维空间中好划分的优点，又回避了高维空间计算量大的缺点，使用原始空间计算。刷了一个小把戏，小聪明。

多项式核函数是映射到 m^2 / 2 维 而高斯核函数是映射到无穷维，但是只用在原来的维度做运算。核函数是不能随便定义的，必须满足一定的条件才行。