bzoj 3527: [Zjoi2014]力 快速傅里叶变换 FFT

题目大意：

给出n个数\(q_i\)定义

\[f_i = \sum_{i<j}{\frac{q_iq_j}{(i-j)^2}} - \sum_{i>j}\frac{q_iq_j}{(i-j)^2}
\]

设\(E_i = \frac{f_i}{q_i}\)，求所有的\(E_i\)

题解:

我们把\(f_i\)代入\(E_i\)的表达式中，有

\[E_i = \sum_{i<j}{\frac{q_j}{(i-j)^2}} - \sum_{i>j}\frac{q_j}{(i-j)^2}
\]

然后我们考虑每个\(q_i\)对\(E_i\)的贡献

我们把贡献做成如下表格，每个格子上的值和列坐标的积是对行坐标的贡献

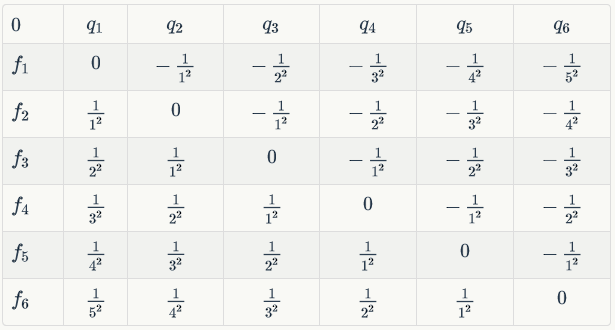
博客园吞我表格，，只能传图了

我们发现正负分布有规律，所以我们把正贡献的负贡献分开计算

我们发现它的每一部分是满足卷积的形式的

即\((q_1,q_2,q_3,...)*(0,\frac{1}{1^2},\frac{1}{2^2},\frac{1}{3^2},...)\)

证明。。。

考虑\(f_3\),卷积后的第三位上，为\(\frac{q_1}{2^2}+\frac{q_2}{1^2}\)恰好是答案

所以FFT上啊

对于负贡献的话把\(q\)数组反过来即可

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
inline void read(int &x){
	x=0;char ch;bool flag = false;
	while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
	while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
inline int cat_max(const int &a,const int &b){return a>b ? a:b;}
inline int cat_min(const int &a,const int &b){return a<b ? a:b;}
const int maxn = 400010;
const double pi = acos(-1);
struct complex{
	double x,y;
	complex(){}
	complex(double a,double b){x=a;y=b;}
	complex operator + (const complex &r){return complex(x+r.x,y+r.y);}
	complex operator - (const complex &r){return complex(x-r.x,y-r.y);}
	complex operator * (const complex &r){return complex(x*r.x-y*r.y,x*r.y+y*r.x);}
	complex operator / (const double &r){return complex(x/r,y/r);}
};
void FFT(complex *x,int n,int p){
	for(int i=0,t=0;i<n;++i){
		if(i > t) swap(x[i],x[t]);
		for(int j=n>>1;(t^=j) < j;j >>= 1);
	}
	for(int m=2;m<=n;m<<=1){
		complex wn(cos(p*2*pi/m),sin(p*2*pi/m));
		for(int i=0;i<n;i+=m){
			complex w(1,0),u;
			int k = m>>1;
			for(int j=0;j<k;++j,w=w*wn){
				u = x[i+j+k]*w;
				x[i+j+k] = x[i+j] - u;
				x[i+j] = x[i+j] + u;
			}
		}
	}
	if(p == -1) for(int i=0;i<n;++i) x[i] = x[i]/n;
}
double q[maxn];
complex a[maxn],b[maxn],c1[maxn],c2[maxn];
int main(){
	int n;read(n);
	for(int i=0;i<n;++i) scanf("%lf",&q[i]);
	int len ;
	for(int i=1;(i>>2) < n;i<<=1) len = i;
	//	printf("%d\n", len);
	for(int i=0;i<n;++i){
		a[i] = complex(q[i],0);
		if(i != 0) b[i] = complex(1.0/i/i,0);
	}
	FFT(a,len,1);FFT(b,len,1);
	for(int i=0;i<len;++i) c1[i] = a[i]*b[i];
	memset(a,0,sizeof a);
	for(int i=0;i<n;++i) a[i] = complex(q[n-i-1],0);
	FFT(a,len,1);
	for(int i=0;i<len;++i) c2[i] = a[i]*b[i];
	//for(int i=0;i<n;++i) printf("%lf %lf || %lf %lf\n",c1[i].x,c1[i].y,c2[i].x,c2[i].y);
	FFT(c1,len,-1);FFT(c2,len,-1);
	for(int i=0;i<n;++i) printf("%.3lf\n",c1[i].x - c2[n-i-1].x);
	getchar();getchar();
	return 0;
}