LDA模型了解及相关知识

什么是LDA？

　　LDA是基于贝叶斯模型的，涉及到贝叶斯模型离不开“先验分布”，“数据（似然）”和"后验分布"三块。贝叶斯相关知识：先验分布 + 数据（似然）= 后验分布。

　　贝叶斯模型通过数学和概率的形式表达, 设 似然(数据)为二项分布：

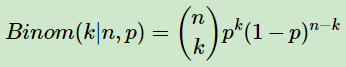
其中p我们可以理解为好人的概率，k为好人的个数，n为好人坏人的总数。似然（数据）较为容易理解，但是先验分布较难，因为要求先验分布和数据（似然）对应的二项分布集合后，得到的后验分布在后面还可以作为先验分布！即是说，我们希望先验分布和后验分布的形式应该是一样的，这样的分布我们一般叫共轭分布。在我们的例子里，希望找到和二项分布共轭的分布。二项分布共轭的分布其实就是Beta分布。Beta分布的表达式为：

其中ΓΓ是Gamma函数，满足Γ(x)=(x−1)!  假设有多个分类而不是二项分布，诸如三维分布。 则在三维时。用三维的Beta分布来表达先验后验分布， 三项的多项分布来表达数据（似然）。

　   三项的多项分布好表达，我们假设数据中的第一类有m1个好人，第二类有m2个坏人，第三类为m3=n−m1−m2个不好不坏的人,对应的概率分别为p1,p2,p3=1−p1−p2，则对应的多项分布为：

　超过二维的Beta分布我们一般称之为狄利克雷(以下称为Dirichlet )分布。也可以说Beta分布是Dirichlet 分布在二维时的特殊形式。从二维的Beta分布表达式，我们很容易写出三维的Dirichlet分布如下：

　　

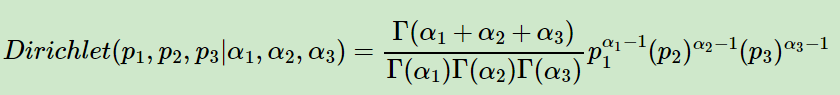
　 多维的狄利克雷(以下称为Dirichlet )分布的概率密度函数就可以写成，用向量表示概率和计数，这样多维的狄利克雷分布可以表示为：Dirichlet(p→|α→),而多项分布可以表示为：multi(m→|n,p→)。

    K维的狄利克雷分布表示：

　而多项分布和Dirichlet 分布也满足共轭关系。

LDA来做什么？

  Hava this question?

(1) 有M段文字，对应第d段文字由Nd 个词组成。

(2) 找到每一段文字的主题分布和每一个主题中词的分布。在LDA模型中，我们需要先假定一个主题数目K，同时所有的分布就都基于K个主题展开。LDA模型的具体表示：

　

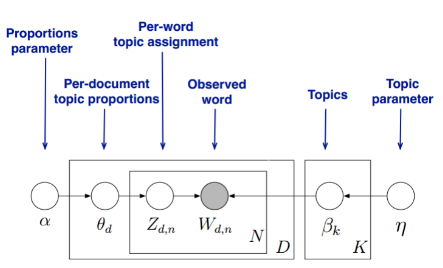
　　LDA假设文字主题的先验分布是Dirichlet分布，即对于任一文字d, 其主题分布θ_d为：

　　

　　  其中，α为分布的超参数，是一个K维向量。

　　LDA假设主题中词的先验分布是Dirichlet分布，即对于任一主题k, 其词分布β_k为：

　　 其中，η为分布的超参数(超参数一般就是根据经验确定的变量。在深度学习中，超参数有：学习速率，迭代次数，层数，每层神经元的个数等，也可以理解为在机器学习的上下文中，超参数是在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。通常情况下，需要对超参数进行优化，给学习机选择一组最优超参数，以提高学习的性能和效果。)，是一个V维向量。V代表词汇表里所有词的个数。

　　对于数据中任一一段文字d中的第n个词，我们可以从主题分布θ_d中得到它的主题编号z_dn的分布为：

　　而对于该主题编号，得到我们看到的词w_dn的概率分布为：

·　　上面的模型中，我们有M个文字主题的Dirichlet分布，而对应的数据有M个主题编号的多项分布，这样(α→θ_d→z_d)就组成了Dirichlet-multi共轭，可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。

　　

　　 如果在第d个文档中，第k个主题的词的个数为：n_d^(k), 则对应的多项分布的计数可以表示。

LDA的模型结构？

　　基于LDA模型可以实现我们想要的每一篇文档的主题分布和每一个主题中词的分布。

　　一般有两种方法，第一种是基于Gibbs采样算法求解，第二种是基于变分推断EM算法求解。

LDA的应用？

使用scikit-learn来学习LDA主题模型在scikit-learn中,LDA主题模型的类在sklearn.decomposition.LatentDirichletAllocation包中，其算法实现主要基于变分推断EM算法。

sklearn.decomposition.LatentDirichletAllocation类库的主要参数：

(1):n_topics:隐含主题数K，需要调参。---->K的大小取决于对我们主题划分的需求。 区分动物、植物，还是非生物粗粒度需求时，K值取较小；如果目标是区分不同的动物以及不同的植物等细粒度需求时，K值需要取很大，上千上万，这就要求训练文档的数量要非常多。

(2):doc_topic_prior: 分析的这段文字主题先验Dirichlet分布θ_d的超参数α。没有这段文字主题分布的先验知识时，设定默认值1/K。

(3)：topic_word_prior:即我们的主题词先验Dirichlet分布β_k的参数η。一般如果我们没有主题分布的先验知识，可以使用默认值1/K。

(4):learning_method: 即LDA的求解算法。有 ‘batch’ 和 ‘online’两种选择。 ‘batch’即变分推断EM算法，"online"即在线变分推断EM算法，在"batch"的基础上引入了分步训练，将训练样本分批，逐步一批批的用样本更新主题词分布的算法。注意： 样本量不大只是用来学习的话用"batch"比较好，这样可以少很多参数要调。而样本太多太大的话，"online"则是首选。

(5): blearning_decay：仅仅在算法使用"online"时有意义，取值最好在(0.5, 1.0]，以保证"online"算法渐进的收敛。主要控制"online"算法的学习率，默认是0.7。一般不用修改这个参数。

(6）:learning_offset：仅仅在算法使用"online"时有意义，取值要大于1。用来减小前面训练样本批次对最终模型的影响。

(7): max_iter ：EM算法的最大迭代次数

(8):total_samples：仅仅在算法使用"online"时有意义， 即分步训练时每一批文档样本的数量。在使用partial_fit函数时需要。

(9）batch_size: 仅仅在算法使用"online"时有意义， 即每次EM算法迭代时使用的文档样本的数量。

(10）mean_change_tol :即E步更新变分参数的阈值，所有变分参数更新小于阈值则E步结束，转入M步。一般不用修改默认值。

(11） max_doc_update_iter: 即E步更新变分参数的最大迭代次数，如果E步迭代次数达到阈值，则转入M步。

注意：主题数KK是LDA主题模型最重要的超参数。

scikit-learn LDA中文主题模型Demo，平台信息：IDE:spyder   Python 3.6.2   内存 8GB 所以支持库均使用Anaconda3按照

1. 首先创建三个txt文件，每个文件中都有一段文字，并先用jieba分词库对每一段txt文字进行分词（jieba相关知识），另行保存,其中涉及到suggest_freq(segment, tune=True) 可调节单个词语的词频的用法等。

2.导入停用词表。

3.接着将词转化为词频向量，由于LDA是基于词频统计的，因此一般不用TF-IDF来做文档。

4.应用得到的所有文档中各个词的词频向量，来使用LDA主题模型。设K=2

 lda = LatentDirichletAllocation(n_topics=2,
                                 learning_offset=50.,
                                 random_state=0)
 docres = lda.fit_transform(cntTf)

5.通过fit_transform函数，我们就可以得到文档的主题模型分布在docres中。而主题词 分布则在lda.components_中。我们将其打印出来。

权重tf-idf权重

相关知识

（1）余弦相似度：在数据分析和数据挖掘中衡量个体间的相似度和类别。最常见的是数据分析中的相关分析，数据挖掘中的分类和聚类算法，如K最近邻（KNN）和K均值（K-Means）。

　　 衡量个体间差异的方法典型方法---->余弦相似度。

　　 设个体A、B都包含了N维的特征，个体A={a_1,a₂................a_n},个体B={b_1,b₂................b_n}

　　比较典型的为(1)距离度量：用于衡量个体间在空间上的距离，距离越远说明相差的差距就越大,典型的有欧氏距离、曼哈顿距离等。

　　　　　　　　(2)相似度度量：即计算个体间的相似程度，与距离度量相反，相似度度量的值越小，说明个体间相似度越小，差异越大。

　　向量空间余弦相似度：余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上。公式如下：

　总结：距离度量衡量的是空间中各点的绝对距离，跟各个点所在的位置坐标（即个体特征维度的数值）直接相关。余弦相似度衡量的是空间向量的夹角，更加的是体现在方向上的差异，而不是位置。如果保持A点的位置不变，B点朝原方向远离坐标轴原点，那么这个时候余弦相似度cosθ是保持不变的，因为夹角不变，而A、B两点的距离显然在发生改变，这就是欧氏距离和余弦相似度的不同之处。

　　欧氏距离：能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异；

　　余弦相似度：是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分用户兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦相似度对绝对数值不敏感）。

　　类似于我进入淘宝频繁的搜索某个关键词，如"外套",随着搜索次数的增加我的欧氏距离不断提高，即我对外套这个关键词的价值不断提高，而不会增加我对外套关键词的余弦相似度，便于区分我的不同类别兴趣，而对单个类别的搜索次数的增加不敏感。

　　问题给的数据的欧式距离是怎么计算的？？给出了权重。