浅谈分词算法（3）基于字的分词方法（HMM）

目录

• 前言
• 目录
• 隐马尔可夫模型（Hidden Markov Model，HMM）
• HMM分词
  • 两个假设
  • Viterbi算法
• 代码实现
  • 实现效果
  • 完整代码
• 参考文献

前言

在浅谈分词算法（1）分词中的基本问题我们讨论过基于词典的分词和基于字的分词两大类，在浅谈分词算法（2）基于词典的分词方法文中我们利用n-gram实现了基于词典的分词方法。在（1）中，我们也讨论了这种方法有的缺陷，就是OOV的问题，即对于未登录词会失效在，并简单介绍了如何基于字进行分词，本文着重阐述下如何利用HMM实现基于字的分词方法。

目录

浅谈分词算法（1）分词中的基本问题

浅谈分词算法（2）基于词典的分词方法

浅谈分词算法（3）基于字的分词方法（HMM）

浅谈分词算法（4）基于字的分词方法（CRF）

浅谈分词算法（5）基于字的分词方法（LSTM）

隐马尔可夫模型（Hidden Markov Model，HMM）

首先，我们将简要地介绍HMM。HMM包含如下的五元组：

• 状态值集合Q={q1,q2,...,qN}，其中N为可能的状态数；
• 观测值集合V={v1,v2,...,vM}，其中M为可能的观测数；
• 转移概率矩阵A=[aij]，其中aij表示从状态i转移到状态j的概率；
• 发射概率矩阵（也称之为观测概率矩阵）B=[bj(k)]，其中bj(k)表示在状态j的条件下生成观测vk的概率；
• 初始状态分布π.

一般地，将HMM表示为模型λ=(A,B,π)，状态序列为I，对应测观测序列为O。对于这三个基本参数，HMM有三个基本问题：

• 概率计算问题，在模型λ下观测序列O出现的概率；
• 学习问题，已知观测序列O，估计模型λ的参数，使得在该模型下观测序列P(O|λ)最大；
• 解码（decoding）问题，已知模型λ与观测序列O，求解条件概率P(I|O)最大的状态序列I。

HMM分词

在（1）中我们已经讨论过基于字分词，是如何将分词转换为标签序列问题，这里我们简单阐述下HMM用于分词的相关概念。将状态值集合Q置为{B,E,M,S}，分别表示词的开始、结束、中间（begin、end、middle）及字符独立成词（single）；观测序列即为中文句子。比如，“今天天气不错”通过HMM求解得到状态序列“B E B E B E”，则分词结果为“今天/天气/不错”。

通过上面例子，我们发现中文分词的任务对应于解码问题：对于字符串C={c1,...,cn}，求解最大条件概率



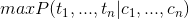
其中，ti表示字符ci对应的状态。

两个假设

在求条件概率



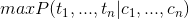
我们利用贝叶斯公式可得



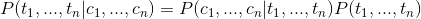
类似于n-gram的情况，我们需要作出两个假设来减少稀疏问题：

• 有限历史性假设: ti 只由 ti-1 决定
• 独立输出假设：第 i 时刻的接收信号 ci 只由发送信号 ti 决定

即如下：





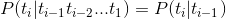
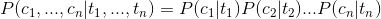
这样我们就可以将上面的式子转化为：



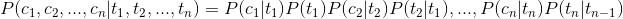
而在我们的分词问题中状态T只有四种即{B,E,M,S}，其中P(T)可以作为先验概率通过统计得到，而条件概率P(C|T)即汉语中的某个字在某一状态的条件下出现的概率，可以通过统计训练语料库中的频率得出。

Viterbi算法

有了以上东东，我们应如何求解最优状态序列呢？解决的办法便是Viterbi算法；其实，Viterbi算法本质上是一个动态规划算法，利用到了状态序列的最优路径满足这样一个特性：最优路径的子路径也一定是最优的。定义在时刻t状态为i的概率最大值为δt(i)，则有递推公式：



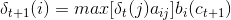
其中，ot+1即为字符ct+1。

代码实现

我们基于HMM实现一个简单的分词器，这里我主要从jieba分词中抽取了HMM的部分[3]，具体逻辑如下：

prob_start.py定义初始状态分布π：

P={'B': -0.26268660809250016,
 'E': -3.14e+100,
 'M': -3.14e+100,
 'S': -1.4652633398537678}

prob_trans.py转移概率矩阵A：

P={'B': {'E': -0.510825623765990, 'M': -0.916290731874155},
 'E': {'B': -0.5897149736854513, 'S': -0.8085250474669937},
 'M': {'E': -0.33344856811948514, 'M': -1.2603623820268226},
 'S': {'B': -0.7211965654669841, 'S': -0.6658631448798212}}

prob_emit.py定义了发射概率矩阵B，比如，P("和"|M)表示状态为M的情况下出现“和”这个字的概率（注：在实际的代码中汉字都用unicode编码表示）；

P={'B': {'一': -3.6544978750449433,
       '丁': -8.125041941842026,
       '七': -7.817392401429855,
    ...}
 'S': {':': -15.828865681131282,
       '一': -4.92368982120877,
       ...}
 ...}

关于模型的训练作者给出了解解释：“来源主要有两个，一个是网上能下载到的1998人民日报的切分语料还有一个msr的切分语料。另一个是我自己收集的一些txt小说，用ictclas把他们切分（可能有一定误差）。 然后用python脚本统计词频。要统计的主要有三个概率表：1)位置转换概率，即B（开头）,M（中间),E(结尾),S(独立成词）四种状态的转移概率；2）位置到单字的发射概率，比如P("和"|M)表示一个词的中间出现”和"这个字的概率；3) 词语以某种状态开头的概率，其实只有两种，要么是B，要么是S。”

在seg_hmm.py中viterbi函数如下：

PrevStatus = {
    'B': 'ES',
    'M': 'MB',
    'S': 'SE',
    'E': 'BM'
}

def viterbi(obs, states, start_p, trans_p, emit_p):
    V = [{}]  # tabular
    path = {}
    for y in states:  # init
        V[0][y] = start_p[y] + emit_p[y].get(obs[0], MIN_FLOAT)
        path[y] = [y]
    for t in range(1, len(obs)):
        V.append({})
        newpath = {}
        for y in states:
            em_p = emit_p[y].get(obs[t], MIN_FLOAT)
            (prob, state) = max(
                [(V[t - 1][y0] + trans_p[y0].get(y, MIN_FLOAT) + em_p, y0) for y0 in PrevStatus[y]])
            V[t][y] = prob
            newpath[y] = path[state] + [y]
        path = newpath

    (prob, state) = max((V[len(obs) - 1][y], y) for y in 'ES')

    return (prob, path[state])

为了适配中文分词任务，Jieba对Viterbi算法做了如下的修改：

• 状态转移时应满足PrevStatus条件，即状态B的前一状态只能是E或者S，...
• 最后一个状态只能是E或者S，表示词的结尾。

与此同时，这里在实现地推公式时，对其求对数，将相乘转化成了相加：



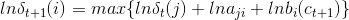
这也就是概率矩阵中出现了负数，是因为对其求了对数。

实现效果

我们写一个简单的自测函数：

if __name__ == "__main__":
    ifile = ''
    ofile = ''
    try:
        opts, args = getopt.getopt(sys.argv[1:], "hi:o:", ["ifile=", "ofile="])
    except getopt.GetoptError:
        print('seg_hmm.py -i <inputfile> -o <outputfile>')
        sys.exit(2)
    for opt, arg in opts:
        if opt == '-h':
            print('seg_hmm.py -i <inputfile> -o <outputfile>')
            sys.exit()
        elif opt in ("-i", "--ifile"):
            ifile = arg
        elif opt in ("-o", "--ofile"):
            ofile = arg

    with open(ifile, 'rb') as inf:
        for line in inf:
            rs = cut(line)
            print(' '.join(rs))
            with open(ofile, 'a') as outf:
                outf.write(' '.join(rs) + "\n")

运行如下：

完整代码

我将完整的代码放到了github上，同上一篇文章类似，这里代码基本是从结巴抽取过来，方便大家学习查阅，模型我也直接拿过来，并没有重新找语料train，大家可以瞅瞅：

https://github.com/xlturing/machine-learning-journey/tree/master/seg_hmm

参考文献

1. 《统计学习方法》 李航
2. 【中文分词】隐马尔可夫模型HMM
3. github jieba
4. 结巴模型的数据是如何生成的
5. 一个隐马尔科夫模型的应用实例：中文分词