BZOJ5120 [2017国家集训队测试]无限之环 费用流

欢迎访问~原文出处——博客园-zhouzhendong

去博客园看该题解

---

题目传送门 - BZOJ5120

---

题意概括

　　原题挺简略的。

---

题解

　　本题好难。

　　听了任轩笛大佬<国家队神犇>的讲课才略会。

　　然而费用流我也是第一次写。而且这题的费用流是特殊的（简化的）。

　　于是我抄了任爷的代码。

　　然而，我因为常量写错，找了一个小时……

　　这里的work和add我都是直接抄的……懒得打，打完还不一定找得出。反正做法是懂了。

　　本题很坑。

　　对于40分，还是比较好拿的，插头dp+滚动（然而我忘记开滚动炸了内存……）就可以了。（代码在最后）

　　据说插头dp+map可以卡到100？

　　这里讲标算做法。

　　我们考虑网络流。

　　对于两个管口相接，我们只需要建一条流量为1的边。

　　但是每一个格子的管子都会转。（除了直线）

　　然而旋转需要费用。

　　所以我们考虑在自身旋转后，建边要加上费用。

　　我们设一个格子的4个接口分别为a，b，c，d，如下图：

　　

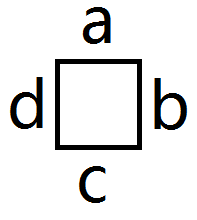
　　如果分情况讨论，那么实在麻烦。实际上我们可以通过自身连边来完成旋转。

　　首先我们考虑管子的本质情况：有7种。那么我们可以有相印的连边方案。（二元组中左边为容量，右边为费用）

　　

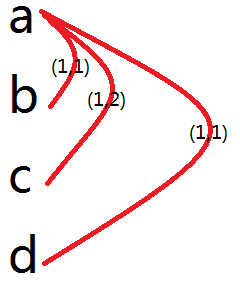
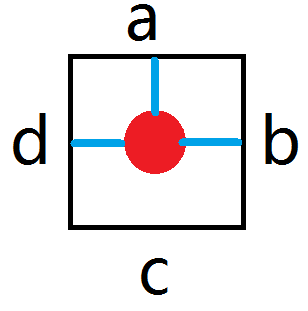
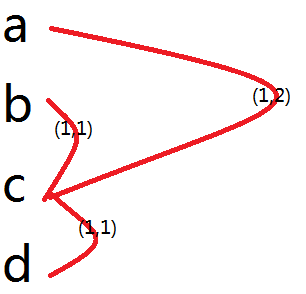
这个……自身建图是不用的。

这个，以及下面的那个建不出图，所以题目说了不能转；哈哈哈哈哈哈哈

　　还有一种情况是空的，那么也是不需要自身转移的。

　　通过自身转移的建图，我们就可以通过费用来完成旋转。

　　然后就是源点的建边，汇点的建边。

　　当然，别忘记，对于每一个格子。

　　然而，我们要记得连上连接接口的边。

　　但是我们发现，这个不仔细考虑会错掉。

　　我们把格子按照(行号+列号)的奇偶性黑白染色。

　　我们发现黑格子的管子一定是接上白格子的。

　　于是我们人为规定，让流从黑格子流向白格子。

　　这样就能确定某一个节点（其实就是方格边上的4点）是从源点流来还是流向汇点了。

　　最后感叹一句：这样做真妙啊！

---

代码

#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <map>
using namespace std;
typedef long long LL;
const int NM=2005,N=8205,M=N*20,Inf=2333333;
int dx[4]={-1, 0, 1, 0};
int dy[4]={ 0, 1, 0,-1};
struct Edge{
    int x,y,z,flow,nxt;
    Edge (){}
    Edge (int a,int b,int c,int d,int e){
        x=a,y=b,z=c,flow=d,nxt=e;
    }
}E[M];
int n,m,S,T,cnt,tot,res,ans,sum;
int id[NM][NM][4],dis[N],vis[N],fst[N],Q[N],pre[N];
int cnt_bit_1(int x){
    int ans=0;
    while (x)
        ans+=x&1,x>>=1;
    return ans;
}
bool check_block(int x,int y){
    return 1<=x&&x<=n&&1<=y&&y<=m;
}
void Add_Edge(int x,int y,int flow,int z){
    E[++cnt]=Edge(x,y,z,flow,fst[x]),fst[x]=cnt;
    E[++cnt]=Edge(y,x,-z,0,fst[y]),fst[y]=cnt;
}
void Add(int x,int y,int flow,int z,int color){
    if (color==1)
        Add_Edge(x,y,flow,z);
    else if (x==S)
        Add_Edge(y,T,flow,z);
    else
        Add_Edge(y,x,flow,z);
}
void work(int i,int j,int type,int dir,int color){
    int *A=id[i][j];
    if (type==1){
        Add(S,A[dir],1,0,color);
        Add(A[dir],A[(dir+1)%4],1,1,color);
        Add(A[dir],A[(dir+2)%4],1,2,color);
        Add(A[dir],A[(dir+3)%4],1,1,color);
    }
    if (type==2){
        Add(S,A[dir],1,0,color);
        Add(S,A[(dir+1)%4],1,0,color);
        Add(A[dir],A[(dir+2)%4],1,1,color);
        Add(A[(dir+1)%4],A[(dir+3)%4],1,1,color);
    }
    if (type==3){
        Add(S,A[dir],1,0,color);
        Add(S,A[(dir+2)%4],1,0,color);
    }
    if (type==4){
        Add(S,A[dir],1,0,color);
        Add(S,A[(dir+1)&3],1,0,color);
        Add(S,A[(dir+2)&3],1,0,color);
        Add(A[dir],A[(dir+3)&3],1,1,color);
        Add(A[(dir+1)&3],A[(dir+3)&3],1,2,color);
        Add(A[(dir+2)&3],A[(dir+3)&3],1,1,color);
    }
    if (type==5){
        Add(S,A[dir],1,0,color);
        Add(S,A[(dir+1)%4],1,0,color);
        Add(S,A[(dir+2)%4],1,0,color);
        Add(S,A[(dir+3)%4],1,0,color);
    }
}
bool SPFA(){
    int head=0,tail=0,qmod=8191;
    int x,y;
    memset(vis,0,sizeof vis);
    memset(dis,63,sizeof dis);
    memset(pre,0,sizeof pre);
    Q[tail=(tail+1)&qmod]=S;
    dis[S]=0,vis[S]=1,pre[S]=0;
    while (head!=tail){
         vis[x=Q[head=(head+1)&qmod]]=0;
         for (register int i=fst[x];i;i=E[i].nxt)
            if (E[i].flow&&dis[x]+E[i].z<dis[y=E[i].y]){
                dis[y]=dis[x]+E[i].z;
                pre[y]=i;
                if (!vis[y]){
                    vis[y]=1;
                    Q[tail=(tail+1)&qmod]=y;
                }
            }
    }
    return dis[T]<Inf;
}
void Flowing(){
    for (register int i=pre[T];i;i=pre[E[i].x])
        E[i].flow--,E[i^1].flow++;
    ans++,res+=dis[T];
}
int main(){
    scanf("%d%d",&n,&m);
    memset(fst,0,sizeof fst);
    tot=sum=0,cnt=1;
    S=++tot,T=++tot;
    for (int i=1;i<=n;i++)
        for (int j=1,x;j<=m;j++){
            scanf("%d",&x);
            for (int k=0;k<4;k++)
                id[i][j][k]=++tot;
            if (x==1) work(i,j,1,0,(i+j)&1);
            if (x==2) work(i,j,1,1,(i+j)&1);
            if (x==3) work(i,j,2,0,(i+j)&1);
            if (x==4) work(i,j,1,2,(i+j)&1);
            if (x==5) work(i,j,3,0,(i+j)&1);
            if (x==6) work(i,j,2,1,(i+j)&1);
            if (x==7) work(i,j,4,0,(i+j)&1);
            if (x==8) work(i,j,1,3,(i+j)&1);
            if (x==9) work(i,j,2,3,(i+j)&1);
            if (x==10) work(i,j,3,1,(i+j)&1);
            if (x==11) work(i,j,4,3,(i+j)&1);
            if (x==12) work(i,j,2,2,(i+j)&1);
            if (x==13) work(i,j,4,2,(i+j)&1);
            if (x==14) work(i,j,4,1,(i+j)&1);
            if (x==15) work(i,j,5,0,(i+j)&1);
            sum+=cnt_bit_1(x);
        }
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
            if ((i+j)&1)
                for (int k=0;k<4;k++){
                    int x=i,y=j;
                    int x_=i+dx[k],y_=j+dy[k];
                    if (!check_block(x_,y_))
                        continue;
                    Add_Edge(id[x][y][k],id[x_][y_][(k+2)%4],1,0);
                }
    ans=res=0;
    while (SPFA())
        Flowing();
    printf("%d",(ans*2==sum)?res:-1);
    return 0;
}

　　

40分的插头dp

#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
using namespace std;
const int N=2005,M=20,S=1<<17,Inf=100000;
int n,m,b[N],a[N],dp[2][S];
int Ha(int a,int b){
	//1<=a<=n,1<=b<=m
	return (a-1)*m+b-1 + 1;
}
void Hab(int v,int &a,int &b){
	v--;
	a=v/m+1;
	b=v%m+1;
}
int rotate(int v,int k){
	return ((v>>k)|(v<<(4-k)))&15;
}
int main(){
	bool tag=0;
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++)
		for (int j=1;j<=m;j++)
			scanf("%d",&b[Ha(i,j)]);
	if (n<m)
		tag=1;
	if (tag==1){
		swap(n,m);
		for (int i=1;i<=n;i++)
			for (int j=1;j<=m;j++)
				a[Ha(i,j)]=rotate(b[(m-j)*n+i],3);/*b[(m-j)*n+i]*/
		// (m-j+1,i)
	}
	else
		for (int i=1;i<=n*m;i++)
			a[i]=b[i];
/*	for (int i=1;i<=n;i++,puts(""))
		for (int j=1;j<=m;j++)
			printf("%d ",a[Ha(i,j)]);*/
	memset(dp,63,sizeof dp);
	dp[0][0]=0;
	int s=1<<(m+1),x1=0,x0=1;
	for (int i=1;i<=n*m;i++){
		x1^=1,x0^=1;
		memset(dp[x1],63,sizeof dp[x1]);
		int x,y,cost;
		Hab(i,x,y);
		for (int j=0;j<s;j++){
			if (dp[x0][j]>Inf)
				continue;
			if (a[i]==5){
				if ((j&1)||!((j>>y)&1))
					continue;
				dp[x1][j]=min(dp[x1][j],dp[x0][j]);
				continue;
			}
			if (a[i]==10){
				if (y==m)
					continue;
				if (!(j&1)||((j>>y)&1))
					continue;
				dp[x1][j]=min(dp[x1][j],dp[x0][j]);
				continue;
			}
			for (int k=0;k<4;k++){
				int dir=rotate(a[i],k);
				int a1=dir&1,a2=(dir>>1)&1,a3=(dir>>2)&1,a4=(dir>>3)&1;
				if ((a1^((j>>y)&1))||(a4^(j&1))||(y==m&&a2))
					continue;
				int j_=((j&(s-2))|a2)&(s-1-(1<<y))|(a3<<y);
				dp[x1][j_]=min(dp[x1][j_],dp[x0][j]+(k==3?1:k));
			}
		}
	}
/*	for (int i=0;i<=n*m;i++,puts(""))
		for (int j=0;j<s;j++)
			printf("%10d ",dp[i][j]);*/
	int ans=dp[x1][0];
	if (ans>Inf)
		ans=-1;
	printf("%d",ans);
	return 0;
}