bzoj 3560 DZY Loves Math V - 线性筛 - 扩展欧几里得算法

给定n个正整数a1,a2,…,an，求

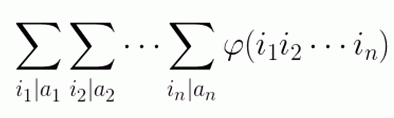
的值（答案模10^9+7）。

Input

第一行一个正整数n。

接下来n行，每行一个正整数，分别为a1,a2,…,an。

Output

仅一行答案。

Sample Input

3
6
10
15

Sample Output

1595

Hint

1<=n<=10^5，1<=ai<=10^7。共3组数据。

---

　　题目大意 (题目过于简洁，完全不需要大意)

　　题目虽然很简洁，但是处处挖着坑等你跳。

　　原计划两个小时把今天讲的例题A完，实际上两个小时都被这道题坑走了(懒惰于重新推公式的下场。。。)

　　//假设读者知道什么是积性函数以及欧拉函数的积性

　　欧拉函数的积性可以表现在这种形式(里面p + 下标都表示互不相同的质数):

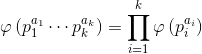
　　所以，我们可以把每个不同的素数分开进行计算贡献，然后再求积(因为我们是把每个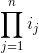像上述形式拆分求phi值，所以是求积)。

　　于是我们成功得到了某个更长的式子:(其中b_(p)i表示a_i中质因子p的指数)

　　由于欧拉函数在此不好运用某些套路快速求结果，所以考虑运用欧拉函数神奇的性质将其拆开。我们知道有关欧拉函数有(同样，p是质数)

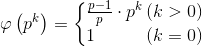
　　虽然当指数为0的时候为特殊情况，但是可以加点黑科技是它不是那么地特殊:

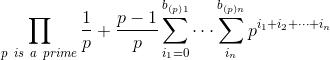
　　是滴，多加了一个1/p就解决了问题。现在继续化简:

$\prod_{p\ is\ a\ prime}\frac{1}{p} + \frac{p - 1}{p}\left ( \sum_{i_{1} = 0}^{b_{\left ( p \right )1}}p^{i_{1}} \right )\cdots \left( \sum_{i_{n} = 0}^{b_{\left ( p \right )n}}p^{i_{n}} \right )$

　　然后得到了：

$\prod_{p\ is\ a\ prime}\frac{1 + \left (p - 1  \right )\left ( \sum_{i_{1} = 0}^{b_{\left ( p \right )1}}p^{i_{1}} \right )\cdots \left( \sum_{i_{n} = 0}^{b_{\left ( p \right )n}}p^{i_{n}} \right )}{p}$

　　此时计算的时间复杂度能够接受。但是由于在模意义下做除法需要乘逆元，由于p是小于1e7的质数，所以一定和1e9 + 7互质，所以逆元一定存在。

　　关于这道题还有很神奇的东西，存有哪些不同的素数用STL(Standard Templates Library Sometimes/Standard TLE/MLE Library)，然而MLE。。。求解释。。。好像和理论算的不太一样。。

　　所以就用一个黑科技。用pair的第一位存是什么素数，第二位存指数。然后sort一下，就可以AC了。

Code

 /**
  * bzoj
  * Problem#3560
  * Accepted
  * Time: 1276ms
  * Memory: 7940k
  */
 #include <bits/stdc++.h>
 #ifndef WIN32
 #define Auto "%lld"
 #else
 #define Auto "%I64d"
 #endif
 using namespace std;
 typedef bool boolean;
 #define smax(a, b) a = max(a, b)
 #define LL long long

 const int moder = 1e9 + ;
 LL mpow(LL a, LL pos) {
     if(pos == )    return ;
     if(pos == )    return a;
     LL temp = mpow(a, pos >> );
     temp = (temp * temp) % moder;
     if(pos & )    temp = (temp * a) % moder;
     return temp;
 }

 void exgcd(LL a, LL b, LL& d, LL& x, LL& y) {
     if(!b) {
         d = a;
         x = , y = ;
     } else {
         exgcd(b, a % b, d, y, x);
         y -= (a / b) * x;
     }
 }

 int inv(int a, int moder) {
     LL d, x, y;
     exgcd(a, moder, d, x, y);
     return (x < ) ? (x + moder) : (x);
 }

 const int limit = ;
 int num = ;
 int prime[];
 boolean vis[limit + ];
 inline void Euler() {
     for(int i = ; i <= limit; i++) {
         if(!vis[i])    prime[num++] = i;
         for(int j = ; j < num && i * prime[j] <= limit; j++) {
             vis[i * prime[j]] = true;
             if((i % prime[j] == ))
                 break;
         }
     }
 }

 int n;
 int* arr;
 int cnt = ;
 pair<int, int> ds[];
 inline void init() {
     scanf("%d", &n);
     arr = new int[(n + )];
     for(int i = ; i <= n; i++) {
         scanf("%d", arr + i);
     }
 }

 LL getSum(int p, int c) {
     LL a = (mpow(p, c + ) - );
     LL b = inv(p - , moder);
     return (a * b) % moder;
 }

 LL res = ;
 inline void solve() {
     for(int i = , x; i <= n; i++) {
         x = arr[i];
         for(int j = ; prime[j] * prime[j] <= x && arr[i] > ; j++) {
             if((arr[i] % prime[j]) == ) {
                 ds[cnt].first = prime[j], ds[cnt].second = ;
                 while((arr[i] % prime[j]) == )
                     arr[i] /= prime[j], ds[cnt].second++;
                 cnt++;
             }
         }
         if(arr[i] > )
             ds[cnt].first = arr[i], ds[cnt++].second = ;
      }
     sort(ds, ds + cnt);

     int p, c;
     for(int id = ; id < cnt; ) {
         p = ds[id].first;
         LL P = ;
         for(int i = id; (id < cnt && ds[i].first == ds[id].first) ? (true) : (id = i, false); i++) {
             c = ds[i].second;
             P = (P * getSum(p, c)) % moder;
         }
         P = ((P * (p - ) + ) % moder) * inv(p, moder) % moder;
         res = (res * P) % moder;
     }
     printf(Auto, res);
 }

 int main() {
     Euler();
     init();
     solve();
     return ;
 }