(原)IOU的计算
转载请注明出处:
http://www.cnblogs.com/darkknightzh/p/9043395.html
参考网址:
https://github.com/deepinsight/insightface/blob/master/src/align/align_megaface.py中IOU的计算。
理解不对的地方敬请谅解。
IOU是两个矩形的交集与两个矩形并集的比值(可以这样理解吧)。
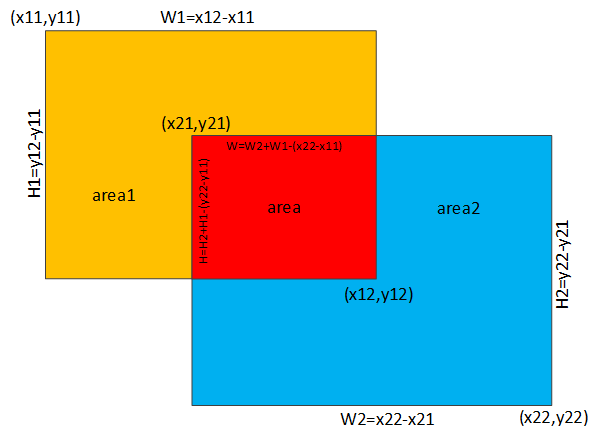
如下图所示:
黄色矩形起点坐标(x11,y11),终点坐标(x12,y12)
蓝色矩形起点坐标(x21,y21),终点坐标(x22,y22)。
则:
黄色矩形宽W1=x12-x11,高H1=y12-y11
黄色矩形宽W2=x22-x21,高H1=y22-y21
两个矩形交集(红色矩形)宽W=W1+W2-(x22-x11)=x12-x11
两个矩形交集(红色矩形)高H=H1+H2-(y22-y11)=y12-y11
红色矩形面积(两个矩形交集)为area=W*H
两个矩形并集为area1+area2-area
如果x12<x21或者y12<y21,说明两个矩形无公共区域,IOU=0;
否则,IOU=area/(area1+area2-area)
(原)IOU的计算的更多相关文章
- vga显示原理即相关计算
行扫描周期:完成一行扫描所需时间: 行时序时间(a,b,c,d,e):完成一个像素点显示得时间 场扫描周期:完成所有行(一帧扫描所需时间) 场时序时间(o,p,q,r,s):完成一行显示得时间,一个完 ...
- 目标检测——IoU 计算
Iou 的计算 我们先考虑一维的情况:令 \(A = [x_1,x_2], B = [y_1, y_2]\),若想要 \(A\) 与 \(B\) 有交集,需要满足如下情况: 简言之,要保证 \(A\) ...
- 使用Python的yield实现流计算模式
首先先提一下上一篇<如何猜出Y combinator>中用的方法太复杂了.其实在Lambda演算中实现递归的思想很简单,就是函数把自己作为第一个参数传入函数,然后后面就是简单的Lambda ...
- 原码 & 反码 & 补码 & 详解
本篇文章讲解了计算机的原码, 反码和补码. 并且进行了深入探求了为何要使用反码和补码, 以及更进一步的论证了为何可以用反码, 补码的加法计算原码的减法. 论证部分如有不对的地方请各位牛人帮忙指正! 希 ...
- CRC(Cyclic Redundancy Check)循环冗余校验码与海明码的计算题
(17)采用CRC进行差错校验,生成多项式为G(X)=X4+X+1,信息码字为10111,则计算出的CRC校验码是 (17) .A.0000 B.0100 C.0010 D.1100试题 ...
- 原代码,反码,解释和具体的补充 Java在>>和>>>差异
前两天分析 HashMap 的 hash 算法的时间,会见 >> 和 >>> 这两个符号.然后检查以下信息,我脑子里在某一时刻.今天遇到,我没想到居然忘 0-0.... ...
- java 变量及数据类型、原码、反码、补码
Java基础——变量及数据类型 变量的概念 内存中的一个存储区域 变量名+数据类型 可在同一类型范围内不断变化 为什么定义变量: 用于不断的存放同一类型的常量,并可以重复使用 使用变量注意: 变量的作 ...
- Java 原码 反码 补码
本篇文章讲解了计算机的原码, 反码和补码. 并且进行了深入探求了为何要使用反码和补码, 以及更进一步的论证了为何可以用反码, 补码的加法计算原码的减法. 论证部分如有不对的地方请各位牛人帮忙指正! 希 ...
- 目标识别(object detection)中的 IoU(Intersection over Union)
首先直观上来看 IoU 的计算公式: 由上述图示可知,IoU 的计算综合考虑了交集和并集,如何使得 IoU 最大,需要满足,更大的重叠区域,更小的不重叠的区域. 两个矩形窗格分别表示: 左上点.右下点 ...
随机推荐
- Github+阿超运算
感谢自己寒假能够稍稍做一点努力. Github个人页面<构建之法阅读笔记二可见>: https://github.com/Heartxy8990 申请教程: http://jingyan. ...
- 图片裁切展示css
.wen_photo{ overflow:hidden;}.wen_photo img{ margin:0; padding:0; width:100%; height: 100%; object-f ...
- docker使用dockerfile 构建redis镜像
FROM redis WORKDIR /data VOLUME /data EXPOSE RUN echo "success---------success" ENTRYPOINT ...
- ubuntu安装nodejs出现./config.gypi错误
报错的内容如下: xxx@xxx [/usr/local/src/node-v0.8.3]# ./configure { 'target_defaults': { 'cflags': [], 'def ...
- BASH if/while/until loop
#/bin/bash ]; then counter=" counter1=" echo "for loop:" $); do echo $i done ); ...
- File类基本用法
[例子1]创建一个新文件. import java.io.*; class hello{ public static void main(String[] args) { File f=new Fil ...
- Android-LruCache与DiskLruCache
Android LruCache与DiskLruCache 学习自 Android开发艺术探索 https://blog.csdn.net/guolin_blog/article/details/28 ...
- Alpha冲刺随笔三:第三天
课程名称:软件工程1916|W(福州大学) 作业要求:项目Alpha冲刺(十天冲刺) 团队名称:葫芦娃队 作业目标:在十天冲刺里对每天的任务进行总结. 随笔汇总:https://www.cnblogs ...
- {}+[]与console.log({}+[])结果不同?从JavaScript的大括号谈起
看到这样一个问题:为什么直接在控制台运行{} + []和用console.log({} + [])输出,两者结果不一样? 于是乎打开chrome的控制台运行了一下: 为什么结果会这样呢?不得已学习一下 ...
- grpc使用客户端技巧
grpc 使用技巧,最近在做的项目是服务端是go语言提供服务使用的是grpc框架. java在实现客户端的时候,参数的生成大部分采用创建者模式.java在接受go服务端 返回数据的时候,更多的是通过p ...
