dp进阶——饥饿的奶牛

饥饿的奶牛oj上n只有1000，过于水，O（n^2）的算法很容易水过，洛谷上这是一道提高加的题，很难啊，所以要好好拿来练习今天写博客再次复习一下，oi最怕遗忘了。

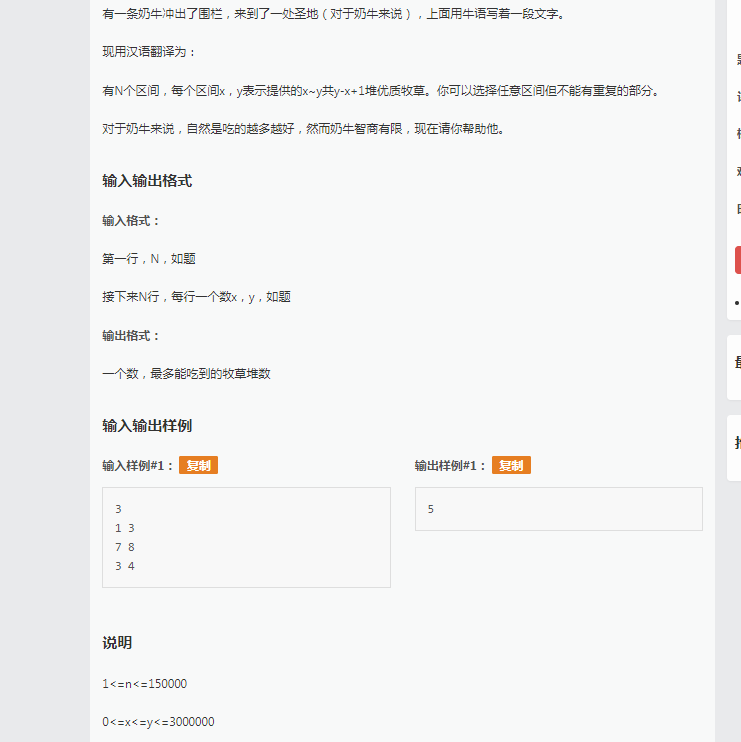
这道题呢实质是一个区间覆盖的dp，首先是设f[i]表示前i个草地所能获得的最大值，这也就很简单的找到了状态转移方程。

如果当前的前j草地和第i草地不相交f[i]=max(f[i],f[j]+s[i].y-s[i]. x+1);最后所要找的就是max(f[i]);这样一道很简单复杂度为O(n^2)的算法被打出来了。

必须要排序因为在进行判断两个区间是否相交的时候直接用s[i].x>s[i].y,排序的目的很显然是为了让每个判断都能把已判断过的边也直接判断出来，要不有可能一些状态是不合法的转移，这样判断就可以是两个区间或和其他已经累加上的区间是否相交了。

#include<iostream>
#include<cstdio>
#include<map>
#include<vector>
#include<iomanip>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
using namespace std;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
const int maxn=;
int n,ans=,f[maxn];
struct bwy
{
    int x,y;
}s[maxn];
int wy(bwy x,bwy y)//闻道玉门犹被遮，应将性命逐轻车
{
    if(x.x==y.x)return x.y<y.y;
    return x.x<y.x;
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    memset(f,,sizeof(f));
    for(int i=;i<=n;i++)
        s[i].x=read(),s[i].y=read();
    sort(s+,s++n,wy);
    for(int i=;i<=n;i++)
    {
        for(int j=;j<i;j++)
            if(s[j].y<s[i].x)f[i]=max(f[i],f[j]+s[i].y-s[i].x+);
    }
    for(int i=;i<=n;i++)
        ans=max(ans,f[i]);
    printf("%d\n",ans);
    return ;
}

这个代码a掉oj上的这道题完全没问题了，洛谷上就TLE了，正常现象。于是考虑到算法的优化。

因为f[i]表示的是第i个草堆所能得到的最大值所以f[i]>=f[j]，这就满足了一个单调性，我可以通过去找离当前的f[i]最近的f[j]且不和f[i]这个区间相交来进行不必要再次循环一遍从0到i来更新最优解，这就是策略，至于咋么找那就是二分了快速查找，二分查找找出这个j值从而进行对i的更新。

和chty学长的一番交流发现自己排序错了，因为在查找的时候是要保证f[j].y<f[i].x.所以假如是全部靠左端点排序的话你的mid值后面的区间是可能仅仅是左端点是小于当前的但是呢其他点的右端点很可能就将其全部涵盖所以你判断当前的点的右端点是出现问题的，这就保证不了两个区间是不相交的了。于是采用右端点排序使右端点递增就可以保证其他的点也小于当前的点的左端点了。

所以应该讲右端点排序然后比的时候是f[j].y<f[i].x这样的话之前的右端点就可以全部小于当前的左端点了，不会有上方情况的发生。右端点排序后dp的时候就可以继承i-1的最优解了因为后面的点不可能和最优解相交且和不优解相交，这样就可以保证啦。。。想了好久的问题终于因为这一个排序所解决。

下面是代码二分专属：

#include<iostream>
#include<cstdio>
#include<map>
#include<vector>
#include<iomanip>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
using namespace std;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
const int maxn=;
struct bwy
{
    int x,y;
}s[maxn];
int wy(bwy x,bwy y)//闻道玉门犹被遮，应将性命逐轻车
{
    if(x.y==y.y)return x.x<y.x;
    return x.y<y.y;
}
int n,f[maxn],ans=;
int find(int x)
{
    int l=,r=x;
    while(l+<r)
    {
        int mid=(l+r)>>;
        if(s[mid].y<s[x].x)l=mid;
        else r=mid;
    }
    if(s[r].y<s[x].x)return r;
    if(s[l].y<s[x].x)return l;
    return -;
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    for(int i=;i<=n;i++)s[i].x=read(),s[i].y=read();
    sort(s+,s++n,wy);
    for(int i=;i<=n;i++)
    {
        int j=find(i);
        if(j!=-)f[i]=max(f[i-],f[j]+s[i].y-s[i].x+);
        else f[i]=max(f[i-],s[i].y-s[i].x+);
    }
    for(int i=;i<=n;i++)
        ans=max(ans,f[i]);
    printf("%d\n",ans);
    return ;
}

其实呢这道题让学长来看就是一个01背包直接看出来，可能对dp十分的熟悉吧。

这里我采用临街表存相同的点的右坐标加上当前的区间的值即可这样的话每次访问到当前的j(正序循环)如果j连边的话就行更新，当然在更新之前要把上个f[i-1]过继下来因为满足了单调性所以可以这样最好f[m]即为最大值。很简单超快的！

#include<iostream>
#include<cstdio>
#include<map>
#include<vector>
#include<iomanip>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
using namespace std;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
const int maxn=;
int n,m,lin[maxn],ver[maxn],len=,nex[maxn],f[maxn];
void add(int x,int y)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
}
struct bwy
{
    int x,y;
}s[maxn];
int main()
{
    //freopen("1.in","r",stdin);
    n=read();
    for(int i=;i<=n;i++)
    {
        s[i].x=read();
        s[i].y=read();
        m=max(m,s[i].y);
        add(s[i].y,s[i].y-s[i].x+);
    }
    for(int i=;i<=m;i++)
    {
        f[i]=f[i-];
        for(int j=lin[i];j;j=nex[j])
        {
            f[i]=max(f[i-ver[j]]+ver[j],f[i]);
        }
    }
    printf("%d\n",f[m]);
    return ;
}

明知不可为而为之！