[0x12] 135.最大子序和【单调队列】

我在知乎上看到一句话，如一道晴天霹雳：

“如果一个选手比你小还比你强，你就可以退役了。”——单调队列的原理

题意

link（more：P1714）

给定一个长度为 \(n\) 的整数序列，从中找出一段长度不超过 \(m\) 的子串，使得子串中所有数的和最大。

其中， \(n,m\leqslant 3\times 10^5\) 。

思路

首先要计算区间和，易想到预处理前缀和（ \(s[i]=\sum\limits_{j=1}^ia[j],s[0]=0\) ）,那么问题可以转化为：找出两个端点 \(l,r(r-l\leqslant m)\) ，使 \(s[r]-s[l]\) 最大。

我们可以先枚举右端点 \(r\) （ \(l\) 也就随之确定），当 \(r\) 固定时，肯定希望 \(s[l]\) 越小越好，问题又可转化为：找出左端点 \(l(l\in[i-m,i-1])\) ，使 \(s[l]\) 最小。

由此，可以易想到一个 \(O(nm)\) 的算法，但显然超时，∵我们把所有情况都进行处理，其实所有 \([i-m,i-1]\) 区间内大于最小值的数都是无用的，但又不可能对区间排序。（属于是火上浇油）

那我们就希望把区间值放到另一个结构里计算，以较高的效率从中得到最小值，且要符合 \(r\) 不断右移，从右边进新值，并从左边出旧值，还要保持单调性。

∴想到用 \(\boxed{单调队列}\) 来维护区间。

假设序列为 \(\{1,-3,5,1,-2,-3\}\) ，则 \(s=\{1,-2,3,4,2,5\}\) 。

已知队列是先进先出的顺序，我们要使进来的值单调（例如可以单调递增），那么我们抽象对比一下两个值 \(x,y\) ，且按顺序进队。如果 \(x\geqslant y\) ，那么 \(x\) 完全就没有用了，把它弹出，继续按照这个逻辑，如图：

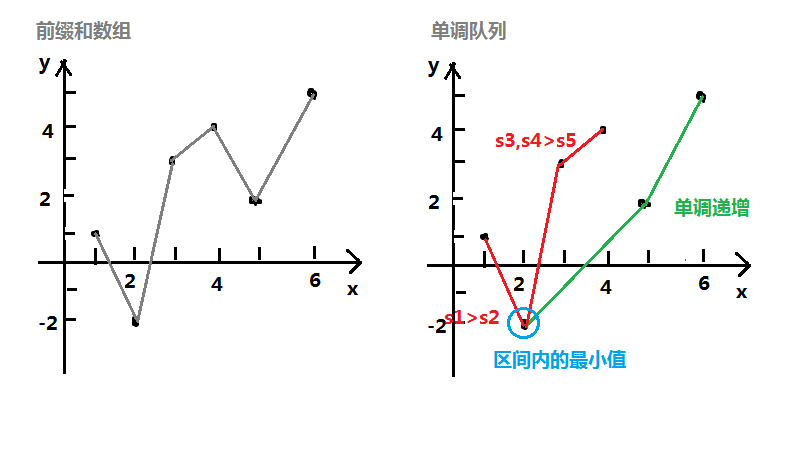
（为便于形象展示，单调队列图中存值，实际代码中，为方便调用，存对应下标）

维护时有两种操作：

• 队头需要弹出值，超过长度限制的值弹出。
• 队尾需要加入值，不断将前面大于自己的数删掉。

可见，维护时每个点最多进队、出队一次，总的时间复杂度就降到了 \(O(n)\) 。

code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=3e5+10;
int n,m;
int Q[N],h,t;
ll s[N];
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		s[i]=s[i-1]+x;
	}
	ll ans=LLONG_MIN;
	for(int i=1;i<=n;i++)
	{
		while(h<=t && Q[h]<i-m) h++;
		ans=max(ans,s[i]-s[Q[h]]);
		while(h<=t && s[Q[t]]>=s[i]) t--;
		Q[++t]=i;
	}
	cout<<ans;
	return 0;
}

总结

单调队列的思想：在决策集合（队列）中及时排除一定不是最优解的选择。