Finance_CAPM&APT

ACCA CAPM:

https://www.bilibili.com/video/BV1KE411j7Ri?from=search&seid=14840285521502157259

投资学 APT

https://www.bilibili.com/video/BV124411Q7We?from=search&seid=14250636441759025443

Lakia CAPM

https://www.bilibili.com/video/BV1u7411B7kc?from=search&seid=14840285521502157259

Lakia APT

https://www.bilibili.com/video/BV1n7411x7HZ

ACCA CAPM

Markowitz 研究风险有效资产的投资，他把所有的风险资产都找到，并对这些资产进行随机组合。有些组合会存在两个或多个风险资产，他就去研究这些组合的标准差和他们的预期回报的关系。最终得到有效前沿，即半圈/最小方差组合。在这个半圈中的组合可以达到最小的风险且最大预期回报，而半圈外的组合则要么风险大，要么收益低。例如，B点的风险比A点的风险高，而B点的收益比D点低。而在圈外的点就不能同时满足其风险与预期回报的关系，所以X点不适用于Markowitz 有效前沿。

　　

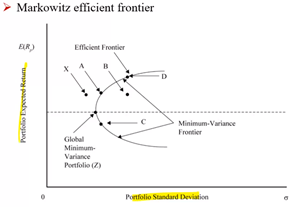
Markowitz通过对市场中不同风险资产组合的风险和回报进行研究，得出有效前沿的理论。只有再有效前沿上的资产组合的风险和收益是相对于其他横轴和纵轴的组合中是最优的。

Capital allocation line

Markowitz没有考虑到无风险资产，所以Sharpe在Markowitz的基础上，引入了无风险资产，他将Rf（无风险资产）与前沿上的组合进行新的组合后形成新的组合。在前沿上的A、P、X组合都是风险资产，所以我们可以把Rf与A、P、X组合形成新的组合，并把他们组成后的线称为资本配置线(p点为最佳风险回报组合)。

　　 

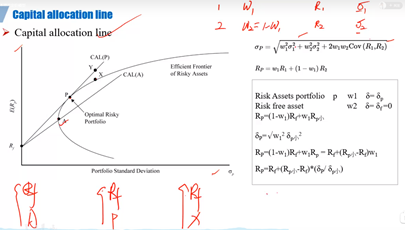
我们将无风险资产与前沿上的风险资产进行组合，看他们组合后的结果是如何的。假设风险资产1的权重为W1，其预期回报为R1和风险为σ1，与风险资产2的权重为W2（W2=1-W1，因为W1+W12=100%），其预期回报为R2和风险为σ2. σ 是总风险包括了系统性风险（系统性风险是由于市场所引起的风险，是不可规避的风险）和非系统性风险（非系统性风险是可以通过多个资产组合来规避的风险）。 我们将风险资产1，2组合后，就形成了新的组合P，其风险为σp和预期回报为Rp，现在我们用风险资产P与无风险资产组合，则可以把整个组合看成为新的风险组合P。将风险资产与无风险资产的W，σ带入得到新的预期回报Rp和风险δp。最终得到R_p=R_f+（R_p小+R_f）/δ_p小*δ_p，其形式类似于y=a+bx，a=Rf，b=（R_p小+R_f）/δ_p小，而x=δ_p。这样，这个组合的风险回报正好是一条直线。例如，我们将Rf与P组合，他们的连线就是他们的风险回报，如果将所有的资产投资于无风险资产，那么得到的回报就是Rf且无风险，但如果将所有的资产投资于P点，那么他的回报就是Rp且风险为δ_p。如果将所有资产分别投资于无风险资产和P组合，那么他的风险回报就会在Rf于Rp的连线上。而连线中的y点，是由于W2可以是负值（代表借入无风险资产并投资于风险资产，如W1=150%，W2=-50%），风险和收益都升高，但他还是服从线性关系。

如果只是投资无风险的组合，则收益为Rf，而投资风险组合，则收益为Rp，然而（R_p小+R_f）/δ_p小是斜率，也可以称为单位风险补偿。无风险可以于前沿上任意一点组合，但只有跟P点组合最好，因为他的斜率最高，即每单位风险补偿就最多。所有引入了无风险资产组合之后，他的最佳风险组合为P点。

Capital Market Line

　　

资本市场线是一条特殊的资本配置线（将所有的资产拿过来，做随机组合找到最优解），它是以某个市场为基础去研究的，如以纳斯达克为市场，去研究它的所有资产组合（可以一两个，多个，整个市场的资产组合）后的风险及预期回报。资本市场线就是无风险与整个市场资产的组合。M点是最优的市场组合。 所以E(Rp)是等于Rf（无风险收益率）加上市场风险每单位的补偿乘以这个风险资产组合的风险。

Capital asset pricing model

　　

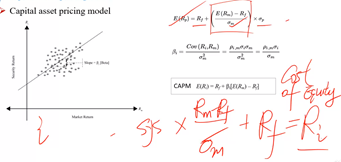
资本市场线是把整个市场做为有效组合与无风险资产组合之后的资本配置线，它是有整个市场风险资产与无风险资产的最优组合。公式可以表示为E(R_p)=R_f + (E(R_m)+R_f）/σ_m*δ_p ，其中(E(R_m)+R_f）/σ_m是市场系统性风险的单位补偿（即斜率），而对于某个资产而言，这只股票的系统性风险乘以整个市场风险的单位补偿，再加上无风险收益率，就可以求出这个股票的Ri。

如何求出这只股票的系统性风险？先找出这个股票的总风险，它包括了系统性风险和无风险，所谓的系统性风险是市场信息所导致的，我们股票的回报和整个市场的回报的相关性ρ_im。每个公司的系统性风险都是不一样的，因为每个公司的股价对市场信息的反映是不一样的，如政府出台清理环境的政策，那么对那些亲和环境的公司就是好消息，反之亦然，但对整个市场是不好不坏。我们要把总风险中的系统性风险剔除出去，这样我们就可以通过找找Ri与Rm的相关系数ρ_im的关系。个股的系统性风险与整个市场的系统性风险是不一样的。市场的系统性风险可以被认为是所有股票平均的系统性风险，但是他们都会对同一个信息做出反映，有的是正相关或负相关，即他们的关联程度。所以Ri同时包含了系统性因素和非系统性因素，而Rm则只有系统性的因素，则ρ_im代表的就是里面有多少个股的风险跟整个市场相关联的。则这个股票的系统性风险就是SYS=ρ_im*σ_i，我们把βi就称为第i个公司的系统性风险，其βi含义为个股的回报与市场的回报的斜率，它衡量的是市场风险与个股的关系。

个股的预期回报E(Ri)是等于无风险回报(Ri)+每单位系统性风险补偿E(Rm)-Rf / σ_m.* 个股的ρ_im，再乘以i的风险σ_i，这样就得到了CAPM资产定价模型。

投资学 APT

APT假设条件：

• 因素模型可以描述收益率，其模型公式为：r_i = E(r_i)+β₁F₁+β₂F₂+β₃F₃+...+e_i）。资产的收益率都会基于以前的收益有一个期望收益率，它的真实的值会围绕这个期望收益率波动，那么它会有一个偏差，这个偏差（F_n）由宏观经济因素决定的，如GDP增长率，IR，PMI值，CPI值等，其中F代表宏观经济因素与实际值的偏差（F₁=r_GDP-E(r_GDP)，而β_i是对某个因素的敏感度，ei代表非系统性风险（是公司个体层面的风险，它必然与F系统风险不相关的。）
• well-diversified portfolio（风险分散化的投资组合，即非系统性风险为0） 可以被构造
• 有限证券不满足因素模型，但着并不影响我们APT的应用。

单因素APT

　　我们以GDP增速为例，r_i = E(r_i)+β₁F₁ +e_i，其中F = r_GDP-E(r_GDP)，F是GDP增速的实际值与期望值的偏差。我们用n种资产构造一个well-diversified portfolio，rp是各种资产收益率的加权值，ω的加总等于1.与此类似，βp、ep、E(rp)都等于各个资产相应的加权和。所以r_p = E(r_p)+β_pF +e_p。由于E(r_p)是常数，所以它的方差为0，他们的方差公式为：σ²_p = β_p²σ_F² +σ²(e_p)，其中F与e_p不相关（不需要考虑他们的协方差），公司与公司之间的e也不相关，而σ²(e_p)通过推到等于0，所以σ²_p = β_p²σ_F²

Lakia CAPM

CAPM是用来估计Asset的收益和风险之间的定量关系。可以用CAPM来判断股票价格的合理性，看看Risk与price是否成正比。

Assumption：

• 投资者都是个人投资者且所有人是理想的（mean-variance optimizer）。
• 没有tax，transaction cost。
• short-sighted，所有人都是短期投资，且市场信息都是有效的。
• 只能投资finacial assets，且可以以free interest来借/贷
• 所有人的expectation都是已知的。这就意味着所有人的行为都是一样的，即大家持有相同的portfolio，只是每个人的风险喜好不同，所以portfolio的持股比例不同。有些人持有的

　　

Line &

• Markowitz effecient frontier：Markowitz通过对市场中不同风险资产组合的风险和回报进行研究，得出有效前沿的理论。只有再有效前沿上的资产组合的风险和收益是相对于其他横轴和纵轴的组合中是最优的。
• CAL(Capital Allocation Line)：Sharpe再Markowitz的基础上，加入了无风险资产。把无风险资产与风险资产组合形成新的组合，并把他们组成后的线称为资本配置线(p点为最佳风险回报组合)。无风险资产与有效前沿的切点是最优组合，M点为Market portfolio，即所有人都会持有的组合，且这跟线被称为 CML。如果只是投资无风险的组合，则收益为Rf，而投资风险组合，则收益为Rp，然而（R_p小+R_f）/δ_p小是斜率，也可以称为单位风险补偿。
• CML(Capital Market Line)：资本市场线是一条特殊的资本配置线（将所有的资产拿过来，做随机组合找到最优解），M点是最优的市场组合。 其公式为E(Rp)是等于Rf（无风险收益率）加上市场风险每单位的补偿乘以这个风险资产组合的风险。

　　

Lakia APT

Multiple factor model 也是研究Risk与Return的关系。

• Sigle factor：
  • 公式：r_i = E(r_i)+β_iF + e_i，ri为stock i，F是指Macro因素：GDP，inflation，Interest rate等等。ei是firm specified Error term。
  • Assumption：
    • E(ei)=0，error term的期望为0.
    • E(ei,es) = 0, ei 与其他的asset无关。
    • e&F无关。
  • E(R) = a + B * E(Factor) , E(R)是average return。

Multiple factor：

• 公式：r_i = E(r_i)+β_iF + e_i。就是将sigle factor变为multiple factor。
• factors之间是无关的，且linear的关系。

　　

CAPM: P_security = R_f + β* risk premium

　　     E(r_i) = R_f + sensitivity to 2 factors (GDP&IR)

　　　　　  = Rf + β_GDP*R_GDP +β_IR * R_IR

　　

APT：我们利用套利的价格来定义均衡。其与CAPM的区别

• APT是一个套利策略：买低卖高。equilibrium指当positive return趋向于0时，就没有套利机会了。effecient，如果市场时effecient说明你的套利机会就是转瞬即逝。
• CAPM: mean-variance rule（每个人都是理性的，都会持有最优组合），APT虽然有risk与return之间的线性关系，但没有mean-variance rule，也就是说APT中，risk和return之间的占比是来源于套利机会。
• CAPM是基于utility theory，而APT认为pricing不单单只是受  影响。
• APT的原则是law of one price（两个东西的是一样的，那么他们的价格也是一样的）。

　　

APT公式: rp = E(r_p) + β_pF + e_p。当β有不相等的时候就会出现套利机会。

　　例1：当β_A=β_B=1，那么我们会选择return高的那个。long 1M A and short 1M B.

　　例2：当βD>βC，那么我们会选择β高的那个，E(r_D)>E(r_C)