蓝桥杯题目——翻硬币无需修改‘*’与’o‘的特殊解法及其所包含的思想

前言

本文介绍蓝桥杯题目——翻硬币的一种无需对字符串进行操作的解法及该解法所包含的思想。

题目信息

桌上放着排成一排的若干硬币。我们用 * 表示正面，用 o 表示反面（是小写字母，不是零）。

比如，可能情形是：**oo***oooo

如果同时翻转左边的两个硬币，则变为：oooo***oooo

现在的问题是：如果已知了初始状态和要达到的目标状态，每次只能同时翻转相邻的两个硬币,那么对特定的局面，最少要翻动多少次呢？

我们约定：把翻动相邻的两个硬币叫做一步操作。

输入格式

两行等长的字符串，分别表示初始状态和要达到的目标状态。

输出格式

一个整数，表示最小操作步数

数据范围

输入字符串的长度均不超过100。

数据保证答案一定有解。

输入样例

**********
o****o****

输出样例

5

解题思维

假设这样一组输入：

**********
o*********

因为每次要翻动两个硬币，想单独地把第一个硬币变成o，就一定会带来副作用（影响其他的硬币），即使这个硬币不在第一个位置。

也就意味着我们用任何方法也不能单独地将一个硬币反转，必须要有另一个同样需要反转的硬币。

因此，题目给的数据中，两个字符串不同之处的数量一定为偶数，否则第一个字符串无论怎样翻转也不能达到第二个字符串（目标）的状态。

思想（1）

因为每个硬币只有正、反两种可能，所以一组硬币（一次反转两个，因此称两个硬币为一组）如果已经被反转一次了，如果再将其反转回来，就会使得这两次反转都无意义。

一般地说，就像同类费解的开关和点灯这种每个位置只有两种选择的问题一样，同一个位置，操作两次，都是无意义的。

在本题中，同一组硬币，我们最多只会翻转一次，拿题目给出的数据举例，我们的目的是把一号和六号的硬币反转成为o。

第一次，我们反转前两个。

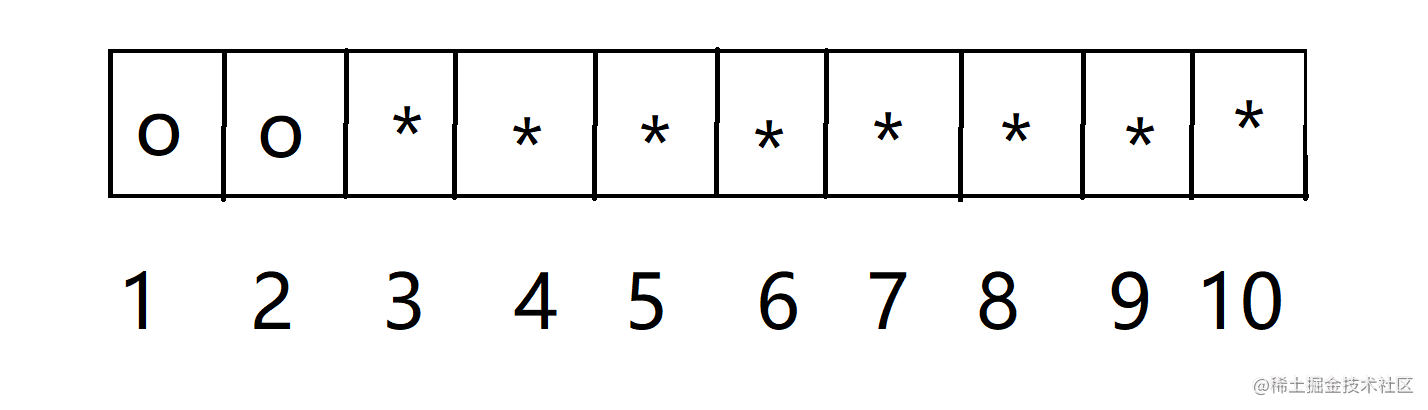
第二次，我们的目的是将2号的o变成*，因为1和2这一组已经被反转一次，因此第二次我们只能选择2和3这一组。

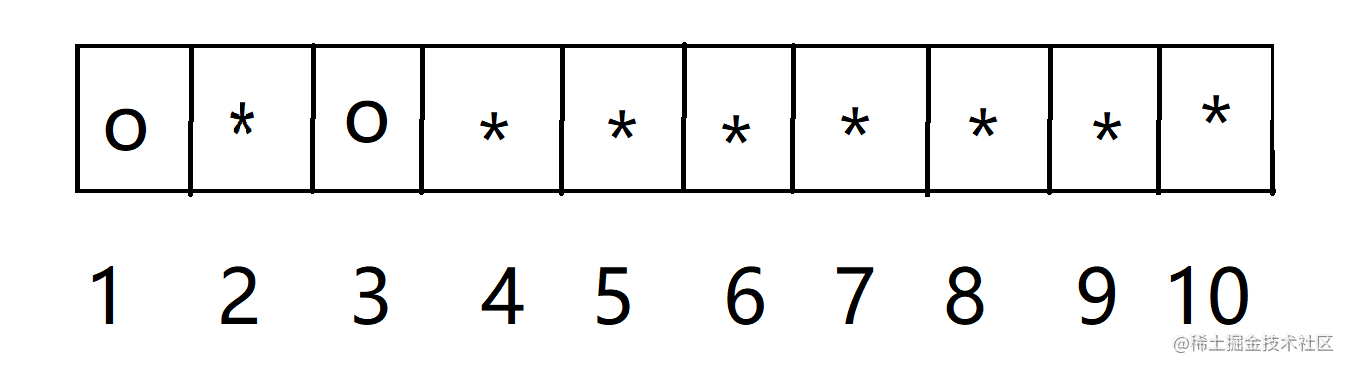
第三次，目的是反转3号，但23这一组已被反转，因此只能反转34这一组。

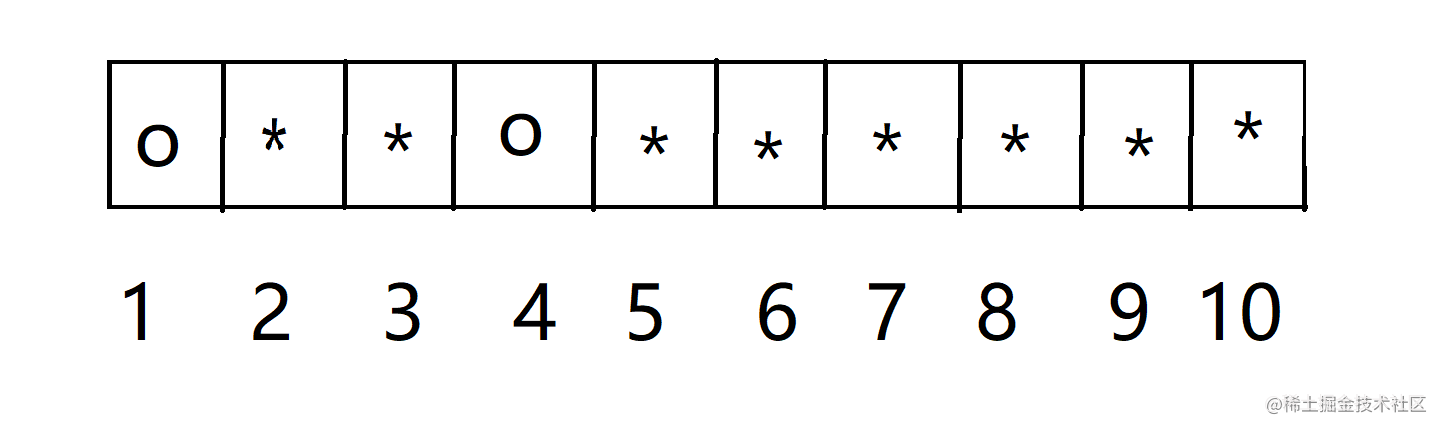
第四次，同理，只能反转45这一组。

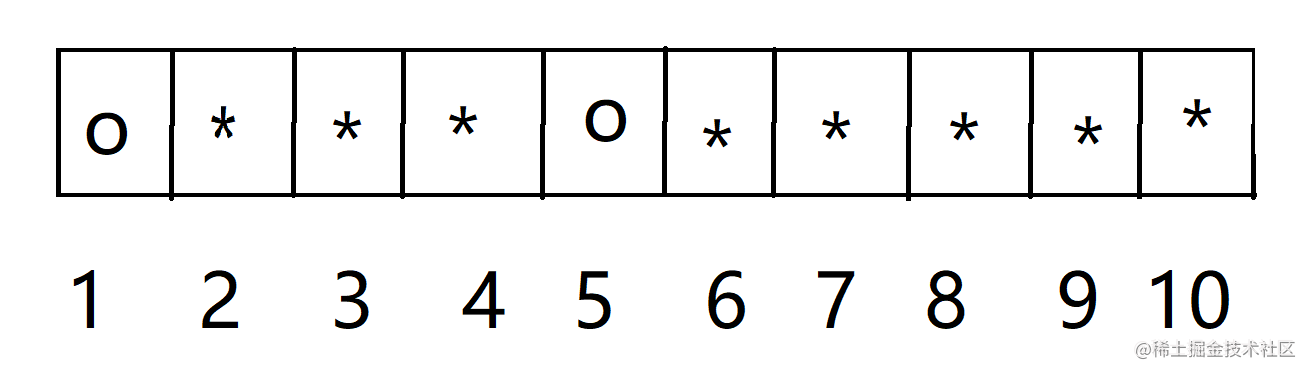
第五次，当反转56这一组时会发现，反转后的状态刚好就是我们所求的状态，这正是刚才解题思维中说到的有另一个需要反转的硬币（6号）来弥补之前的硬币（1号）反转所带来的副作用。

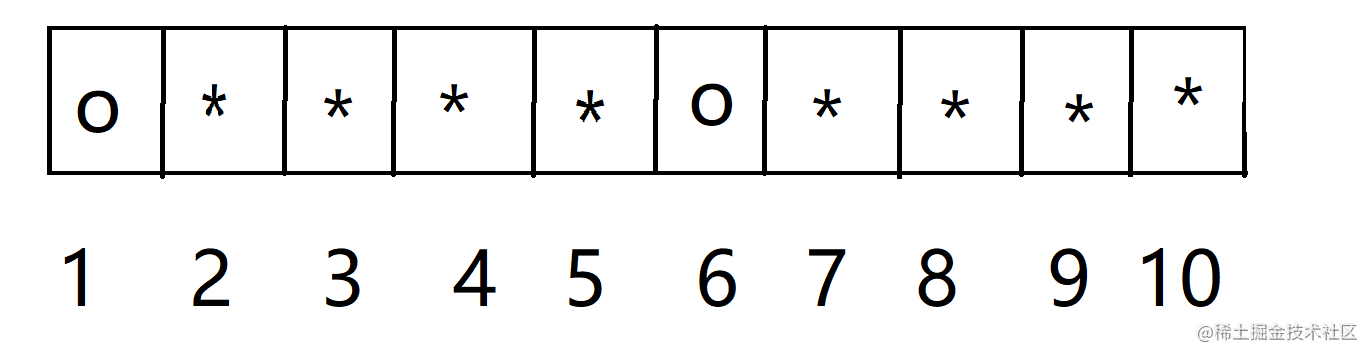
此时你会发现，从1号到6号，其包含的每一组我们都反转了一次，其间的每一个硬币我们都反转了两次，只有这样才能刚刚好使得两个不同之处变为相同。

原因： 其间的硬币反转两次，相当于没反转；其包含的最开始和最后一个硬币，只反转了一次，因此改变的正反面。

因此，对于这题我们只需要找到每两个不同之处之间有多少个硬币，就可以推算出将这两个不同之处同时反转，需要消耗几步。

思想（2）

如果做题时没有发现每同时反转两个不同之处所消耗的步数等于其间的硬币数+1这条规律，那么大概率会用模拟法做，那无疑就使代码更加复杂。

一数曾说过下文类似的一句话：像这种看起来很简单，但是数据很大，暴力法做不了的；看起来像一般性题，但一般性方法做不了的，通常在题目中都有隐含的条件没有发现，一旦发现，此类题目将特别简单。

代码实现

首先，写出主函数和用来输入输出的函数。

int main()
{
	char str1[120];
	gets_s(str1);
	char str2[120];
	gets_s(str2);

	int time =sta(str1, str2);
	printf("%d", time);
	return 0;
}

随后对sta函数进行实现。

我们要统计的数目是每一组不同之处之间的硬币数，因此设置一个变量flag，当其为1时代表遇到了一组不同中的第一个不同，此时开始统计数目，当其为-1时，代表遇到了一组不同中的第二个不同，此时不统计数目。

int sta(char* str1, char* str2)
{
	int count = 0;
	int flag = -1;//是否开启统计
	while (*str1 != '\0')
	{
		if (*str1 != *str2)
		{
			flag *= -1;
		}
		if (flag==1)
		{
			count++;
		}
		str1++;
		str2++;
	}
	return count;

}

可见，代码中并没有对字符串的任何操作，极大地减轻了代码量。

思想（3）

在实现sta函数时，并没有将flag的初始值设为0，而是设为了-1。

这样做可以在开启或关闭统计时直接让其乘以-1即可，不用再判断flag此时是哪一种情况。

亦或者在用模拟法的时候，* 表示正面，o 表示反面，那么你在反转时要先判断当前位置是 * 还是 o，但是如果用1表示正面，-1表示反面，你在反转的时候不需要判断，只需要让其乘以-1即可。

亦或者像费解的开关那样，用1表示开，0表示关，这样你在打开或关闭的时候，只要让其赋值为自身的非即可，不必额外判断当前的情况。

---

感谢您的阅读与耐心~ 如有错误烦请指出~ 谢谢