Jamie and Tree （dfs序 + 最近公共祖先LCA）

题面

题解

我们求它子树的权值和，一般用dfs序把树拍到线段树上做。

当它换根时，我们就直接把root赋值就行了，树的结构不去动它。

对于第二个操作，我们得到的链和根的相对位置有三种情况：

设两点为A、B，LCA 为 C，一个点x的dfs序为ld[x]，从它的子树里出来时的dfs序为rd[x]

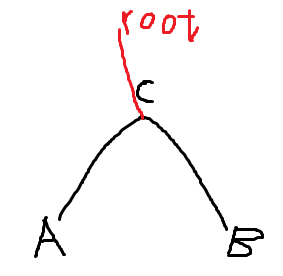
第一种情况，根是C的祖先，他的实际操作区间就是原本的子树区间[ld[C]，rd[C]]

第二种情况，根在A、B路径上，那么它的实际LCA就应该是root，操作区间为[1,n]

第三种情况，根在C的子树上，A、B路径外，那么我们实际上要找到红色路径上最上方的点D

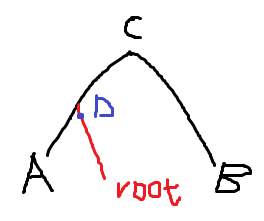
点D的父亲刚好在A、B路径上，那么实际子树就是除了D子树外的其他部分，操作区间为[1，ld[D])∪(rd[D],n]

把相应区间在线段树上区间加就行了。

3操作就相当于A=B的路径。

ＣＯＤＥ

#include<cstdio>
#include<cstring>
#include<iostream>
//-----------F1
using namespace std;
#include<algorithm>
#include<cmath>
//-----------F2
#include<vector>
#include<stack>
#include<queue>
#include<map>
#define MAXN 100005
#define LL long long
#define lowbit(x) (-(x) & (x))
#define ENDL putchar('\n')
//#pragma GCC optimize(2)
//#pragma G++ optimize(3)
//#define int LL
char char_read_before = 1;
inline int read() {
	int f = 1,x = 0;char s = char_read_before;
	while(s < '0' || s > '9') {if(s == '-') f = -1;s = getchar();}
	while(s >= '0' && s <= '9') {x = x * 10 - '0' + s;s = getchar();}
	char_read_before = s;return x * f;
}
LL zxy = 1000000007ll; // 用来膜的
int n,m,i,j,s,o,k,root = 1;
LL a[MAXN],da[MAXN];
LL tre[MAXN<<2],lz[MAXN<<2],M;
inline void maketree(int n) {
	M = 1; while(M < n+2) M <<= 1;
	for(int i = 1;i <= n;i ++) {
		tre[i + M] = da[i];
	}
	for(int i = M-1;i > 0;i --) {
		tre[i] = tre[i<<1] + tre[i<<1|1];
	}
}
inline void addtree(int l,int r,LL y) {
	if(l > r) return ;
//	printf("add %lld to [%d,%d]\n",y,l,r);
	int s = M + l - 1,t = M + r + 1;
	int ls = 0,rs = 0,sz = 1;
	while(s || t) {
		tre[s] += ls * y;
		tre[t] += rs * y;
		if((s>>1) ^ (t>>1)) {
			if(!(s & 1)) tre[s^1] += y * sz,lz[s^1] += y,ls += sz;
			if(t & 1) tre[t^1] += y * sz,lz[t^1] += y,rs += sz;
		}
		s >>= 1; t >>= 1; sz <<= 1;
	}
	return ;
}
inline LL findtree(int l,int r) {
	if(l > r) return 0;
	int s = M + l - 1,t = M + r + 1;
	int ls = 0,rs = 0,sz = 1;
	LL ans = 0;
	while(s || t) {
		ans += ls * lz[s];
		ans += rs * lz[t];
		if((s>>1) ^ (t>>1)) {
			if(!(s & 1)) ans += tre[s^1],ls += sz;
			if(t & 1) ans += tre[t^1],rs += sz;
		}
		s >>= 1; t >>= 1; sz <<= 1;
	}
	return ans;
}
vector<int> g[MAXN];
int dfn[MAXN],rd[MAXN],cnt;
int fa[MAXN][18],d[MAXN];
inline void dfs(int x,int fat) {
	dfn[x] = ++ cnt;
	da[cnt] = a[x];
	fa[x][0] = fat;
	d[x] = d[fat] + 1;
	for(int i = 1;i <= 17;i ++) fa[x][i] = fa[fa[x][i-1]][i-1];
	for(int i = 0;i < g[x].size();i ++) {
		if(g[x][i] != fat) {
			dfs(g[x][i],x);
		}
	}
	rd[x] = cnt;
	return ;
}
inline int lca(int a,int b) {
	if(d[a] < d[b]) swap(a,b);
	if(d[a] > d[b]) {
		for(int i = 17;i >= 0;i --) {
			if(d[fa[a][i]] >= d[b]) a = fa[a][i];
		}
	}
	if(a == b) return a;
	for(int i = 17;i >= 0;i --) {
		if(fa[a][i] ^ fa[b][i]) {
			a = fa[a][i];
			b = fa[b][i];
		}
	}
	return fa[a][0];
}

signed main() {
	n = read();m = read();
	for(int i = 1;i <= n;i ++) {
		a[i] = read();
	}
	for(int i = 2;i <= n;i ++) {
		s = read();o = read();
		g[s].push_back(o);
		g[o].push_back(s);
	}
	dfs(1,0);
	maketree(n);
	for(int i = 1;i <= m;i ++) {
		k = read();
		if(k == 1) {
			root = read();
		}
		else if(k == 2) {
			s = read();o = read();k = read();
			int lc = lca(s,o);
			if(d[lca(root,lc)] < d[lc]) {
				addtree(dfn[lc],rd[lc],(LL)k);
			}
			else if(lca(root,s) == root || lca(root,o) == root) {
				addtree(1,n,(LL)k);
			}
			else {
				int lt = lca(root,s),rt = lca(root,o);
				int fn = root;
				for(int i = 17;i >= 0;i --) {
					if(d[fa[fn][i]] > max(d[lt],d[rt])) {
						fn = fa[fn][i];
					}
				}
				addtree(1,dfn[fn] - 1,(LL)k);
				addtree(rd[fn] + 1,n,(LL)k);
			}
		}
		else if(k == 3) {
			s = read();
			if(lca(s,root) ^ s) {
				printf("%lld\n",findtree(dfn[s],rd[s]));
			}
			else if(s ^ root) {
				int fn = root;
				for(int i = 17;i >= 0;i --) {
					if(d[fa[fn][i]] > d[s]) fn = fa[fn][i];
				}
				printf("%lld\n",findtree(1,dfn[fn] - 1) + findtree(rd[fn] + 1,n));
			}
			else printf("%lld\n",findtree(1,n));
		}
	}
	return 0;
}