关于基础RMQ——ST算法

RMQ，Range Maximum/Minimum Query，顾名思义，就是询问某个区间内的最大值或最小值，今天我主要记录的是其求解方法——ST算法

相对于线段树，它的运行速度会快很多，可以做到O(log n)的预处理和O(1)的查询，不足就是无法进行区间修改，这个一会就会提及

我将从四个方面进行记录：

1、ST的算法流程

其实与DP有很大的相似性，用 a[1,2,....,n] 来记录整组数据，设 f[i,j] 代表从 a[i] 到 a[i+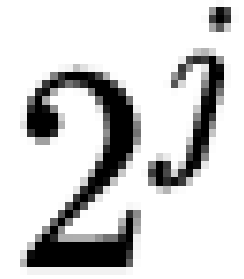-1] 之间所有元素的最大值。

不难发现，其实这个区间就有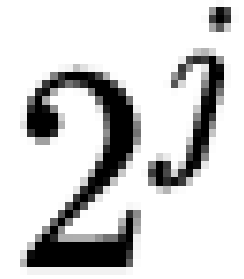个元素。现在我们将这些元素平均分为两部分，那么每部分就是个元素，而这两个集合就可以写成：

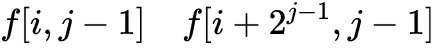
那么整个区间的最大值就转换成了两个区间最大值的较大值，根据动态规划的最优化原理，就可以轻松的写出状态转移方程：

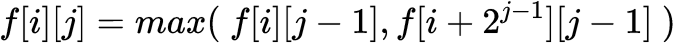
边界条件就是：

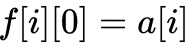
2、询问

要想要找出区间 [x,y] 的最大值，与刚才讲的方法类似，找出最大的 a 满足：

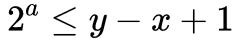
至于为啥不能是直接取等于，是因为取等于时不一定是整数。

所以不一定是正好是整个区间的一半，会出现以下这种情况：

不过That's OK，因为就算区间有重叠也不会影响最大值的确定，但是如果进行区间的操作的话可能就不适用了，因为重叠的部分会被操作两次，这明显不公平！这也是我最开始的时候对ST进行批判的原因，也是ST算法只适用于求区间最值的原因。

3、代码实现

刚才其实都讲的差不多了，不做过多解释：

 1 #include<cstdio>
 2 #include<cmath>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6 const int NN=1e6+5;
 7 int f[NN][21];//21位就差不多了，2的21次方超过了1e6
 8
 9 inline int read()//快读
10 {
11     char ha=getchar();
12     int x=0,sign=1;
13     while(ha<'0'||ha>'9')
14     {
15         if(ha=='-')
16         {
17             sign=-1;
18         }
19         ha=getchar();
20     }
21     while(ha>='0'&&ha<='9')
22     {
23         x=x*10+ha-'0';
24         ha=getchar();
25     }
26     return x*sign;
27 }
28
29 int Query(int l,int r)
30 {
31     int logg=log2(r-l+1);
32     int haha=max(f[l][logg],f[r-(1<<logg)+1][logg]);
33     return haha;
34 }
35 int main()
36 {
37     int N=read(),M=read();
38     for(int i=1;i<=N;i++)//初始化，只有一个数的区间最大值就是它本身
39     {
40         f[i][0]=read();
41     }
42     for(int j=1;j<=21;j++)//开始DP找最大值
43     {
44         for(int i=1;i+(1<<j)-1<=N;i++)
45         {
46             f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
47         }
48     }
49     for(int i=1;i<=M;i++)
50     {
51         int l=read(),r=read();
52         int ans=Query(l,r);
53         printf("%d\n",ans);
54     }
55     return 0;
56 }

四、例题精讲

敬请期待！

To Be Continued...