java中的递归机制

本文主要讲述java中的递归机制。

示例1，递归代码如下：

public class Recursion01 {
    public static void main(String[] args) {
        T t = new T();
        t.test(4);
    }

}
class T {
    public void test(int n) {
        if(n > 2) {
            test(n-1);
        }
        System.out.println(n);
    }
}

jvm处理递归机制如下图所示：

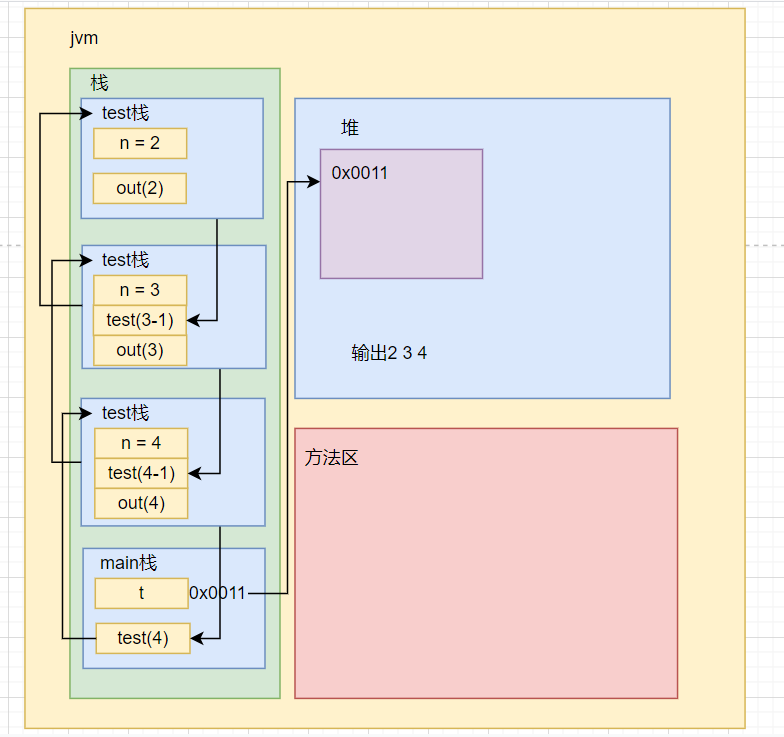
运行结果如下：

示例2，递归代码如下：

public class Recursion01 {
    public static void main(String[] args) {
        T t = new T();
        t.test(4);
    }
}
class T {
    public void test(int n) {
        if(n > 2) {
            test(n-1);
        }else {
            System.out.println(n);
        }
    }
}

jvm处理递归机制如下图所示：

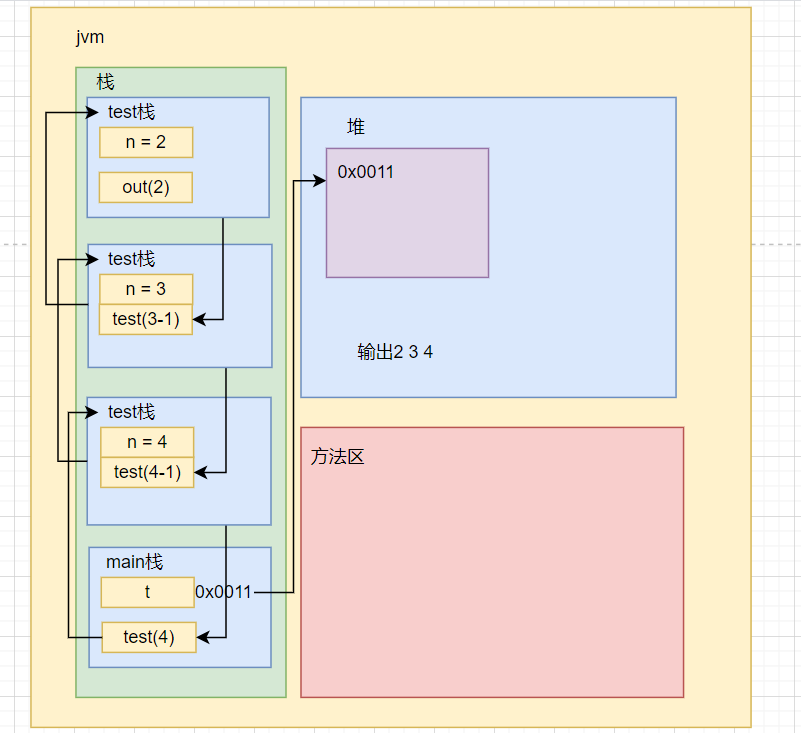
运行结果是2。

注意示例1和示例2的区别。示例1是执行test方法，就会打印当前的n，示例2是做出判断小于或者等于2的打印当前的n。

课堂练习：

1.斐波那契数列

public class Recursion02 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int key = scanner.nextInt();
//        int num = new NumUtils().fun(key);
//        if(num >= 1) {
//            System.out.println("当n="+key+"时,对应的斐波那契数列:"+num);
//        }else {
//            System.out.println("输入数据无效");
//        }
        new NumUtils().Fibonacci(key);
    }

}

class NumUtils {
    // 斐波那契数列中指定索引的值
    public int fun(int n) {
        if(n > 2) {
            return fun(n-1)+fun(n-2);
        }
        if(n == 1 || n == 2){
            return 1;
        }
        return -1;

    }

    // 打印斐波那契数列
    public void Fibonacci(int n) {
        int a = 0,b = 1,c;
        if(n > 1) {
            System.out.print(1+" ");
            for(int i =1;i<n;i++) {
                c = a + b;
                a = b;
                b = c;
                System.out.print(c +" ");
            }
        }else {
            System.out.println("输入数据有误");
        }
    }
}

运行结果：

2.猴子吃桃问题：

/* 吃桃规则：每次吃剩余桃子的一半，加一。
 * day10,还有1个桃
 * day9,还有4 = (day10 + 1)*2个桃
 * day8,还有10 = (day9 + 1)*2个桃
 * ...
 */

public class Recursion03 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int day = scanner.nextInt();
        int res = new Monkey().Peach(day);
        if(res != -1) {
            System.out.println("当day="+day+"时,还有"+res+"个桃");
        }else {
            System.out.println("输入天数有误");
        }

    }
}
class Monkey{

    public int Peach(int day) {

        if(day == 10) {
            return 1;
        }
        if(day >= 1 && day <10) {
            return (Peach(day + 1)+1)*2;
        }

        return -1;
    }
}

3.迷宫问题

public class Migong {
    public static void main(String[] args) {

        int [][] map = new int[8][7];

        MiGongGraph graph = new MiGongGraph();
        graph.CreateGraph(map);
        graph.findWay2(map, 1, 1);

        System.out.println("===当前地图===");
        for(int  i =0;i<map.length;i++) {
            for(int j = 0;j<map[0].length;j++) {
                System.out.print(map[i][j]+" ");
            }
            System.out.println();
        }

    }

}

class MiGongGraph {
    public void CreateGraph(int[][] map) {
        for(int j = 0;j < map[0].length;j++) {
            map[0][j] = 1;
            map[map.length-1][j] = 1;
        }

        for(int i = 0;i<map.length;i++) {
            map[i][0] = 1;
            map[i][map[0].length-1] = 1;
        }
        map[3][1] = 1;
        map[3][2] = 1;
        map[2][2] = 1;
    }

    /*
     * 0表示还没有走，不是障碍物，
     * 1表示障碍物，
     * 2表示走过，无法确定是否是死路
     * 3表示走过，但是走不通，是死路。
     *
     * 走路的顺序，右->下->上->左
     */
    public boolean findWay(int [][] map,int i,int j) {
        // map[5][6] = 2时，说明已经走出迷宫。
        if(map[6][5] == 2) {
            return true;
        }else {
            // 递归体:
            // 判断当前坐标是否已经走过
            if(map[i][j] == 0) {
                // 没有走过，则将其对应的二维数组的值置为2
                map[i][j] = 2;

                // 沿着这个点，按照顺序，走路。
                // 首先是这个点的右边
                if(findWay(map, i, j+1)) {
                    return true;
                // 接着是这个点的下边
                }else if(findWay(map, i+1, j)) {
                    return true;
                // 接着是这个点的上边
                }else if(findWay(map, i-1, j)) {
                    return true;
                // 最后是这个点的左边
                }else if(findWay(map, i, j-1)) {
                    return true;
                }else {
                    // 由于该点的右->下->上->左，都不能走通，则该点是死路，置为3。
                    map[i][j] = 3;
                    return false;
                }
            // 已经走过，不回溯。
            }else {
                return false;
            }
        }
    }

    public boolean findWay2(int [][] map,int i,int j) {
        if(map[6][5] == 2) {
            return true;
        }else {
            // 递归体:
            // 判断当前坐标是否已经走过
            if(map[i][j] == 0) {
                // 没有走过，则将其对应的二维数组的值置为2
                map[i][j] = 2;

                // 沿着这个点，按照顺序，走路。
                // 首先是这个点的下边
                if(findWay(map, i+1, j)) {
                    return true;
                // 接着是这个点的右边
                }else if(findWay(map, i, j+1)) {
                    return true;
                // 接着是这个点的上边
                }else if(findWay(map, i-1, j)) {
                    return true;
                // 最后是这个点的左边
                }else if(findWay(map, i, j-1)) {
                    return true;
                }else {
                    // 由于该点的右->下->上->左，都不能走通，则该点是死路，置为3。
                    map[i][j] = 3;
                    return false;
                }
            // 已经走过，不回溯。
            }else {
                return false;
            }
        }
    }
}

4.汉诺塔问题：

汉诺塔规则：a,b,c三柱，将从上往下看由小到大的塔，由a柱搬到c柱。塔仍保持从上往下看，由小到大。

public class HanNoTa {
    public static void main(String[] args) {
        Tower tower = new Tower();
        tower.Method(3, 'A', 'B', 'C');
    }

}

class Tower {

    // num是盘子的总数,a,b,c是指代三根柱子。
    public void Method(int num,char a,char b,char c) {
        if(num == 1) {
            System.out.println(a +"->"+c);
        }else {
            // 将汉诺塔分成最后一个盘和上面的盘,两个部分
            // 先将上面的盘，借助c柱，由a柱搬到b柱
            Method(num-1, a, c, b);
            // 此时只剩下最后一个盘，直接由a柱搬到c柱
            System.out.println(a+"->"+c);
            // 还需要将上面的盘，由b柱移动到c柱
//            System.out.println(b+"->"+c);
            // 将上面的盘子，借助a柱，由b柱搬到c柱。
            // 不能直接由b柱到c柱，违背汉诺塔的规则。
            Method(num-1, b, a, c);

        }
    }
}