LGV算法 CodeForces 348D + 牛客多校 A Monotonic Matrix

定理（Lindström–Gessel–Viennot lemma）很简单：

学的时候忘了大的行列式怎么算的了。。

然后就可以写题了：

第一道：CodeForces-348D（链接https://vjudge.net/problem/CodeForces-348D）

题意给你个n*m的方阵，有一些点无法通过，然后求从(1,1)到(n,m)走两条路，并且两条路不相交的方案数。

题解：只能向右或者向下走，那么起始点肯定一个向左一个向右，结束点肯定一个从上方过来，一个从左方过来，那么题就成了两个点（1，2）（2，1）到两个点（n-1，m）（n，m-1）。就能写了。

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define met(a, b) memset(a, b, sizeof(a))
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define bep(i, a, b) for(int i = a; i >= b; i--)
#define re return 0
using namespace std;
const ll mod = 1e9 + 7;
const double PI = acos(-1);
const ll INF = 2e18+1;
const int inf = 1e9 + 15;
const double eps = 1e-7;
const int maxn = 1e6 + 5;
ll d[3003][3003], p[3003][3003];
string ma[3003];
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int n, m; cin >> n >> m;
    n--, m--;
    rep(i, 0, n) cin >> ma[i];
    d[0][0] = p[0][0] = 1;
    rep(i, 0, n){
        rep(j, 1, m){
            if(ma[i][j] == '.'){
                if(i) d[i][j] += d[i-1][j];
                if(j) d[i][j] += d[i][j-1];
                d[i][j] %= mod;
            }
        }
    }
    rep(i, 1, n){
        rep(j, 0, m){
            if(ma[i][j] == '.'){
                if(i) p[i][j] += p[i-1][j];
                if(j) p[i][j] += p[i][j-1];
                p[i][j] %= mod;
            }
        }
    }
    cout << ((d[n-1][m]*p[n][m-1])%mod - (d[n][m-1]*p[n-1][m])%mod + mod) % mod << endl;
    re;
}

牛客多校的题Monotonic Matrix （链接https://vjudge.net/problem/Gym-247727A）

题意：n*m的格子，每个格子可以填0，1，2，要求保证每行每列都是非递减，求可填充的方案数。

题解：

直接上图

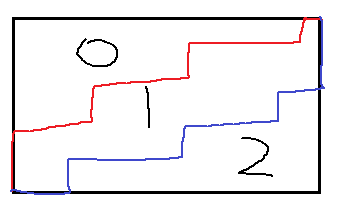
也就是找两条线，一条01分割线，一条12分割线。这样就和LGV有联系了，但是LGV求的是不相交（重合也不行），而这题是可以重合的。如下图

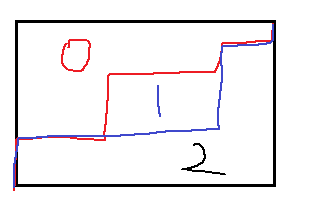
为了能用LGV必须让上图变成不重合的，那么就可以平移一个线，可以把红线的起始点终点向左向上平移一格，或者把蓝线的起始点终点向右向下平移一个格。

我们平移红线，就变成了：

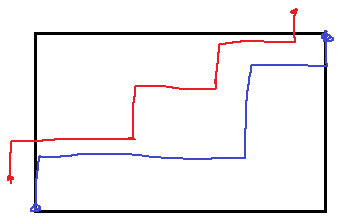可以发现其实变成了这样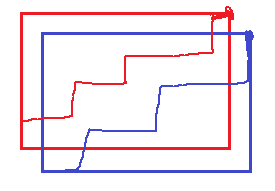：这种可以用LGV求出来不相交的，就等价于上边含有重合的。如果不太理解可以想一下这种求出来的所有方案的情景，把红色向右下移动一格，不就是含有重合的所有方案数吗。

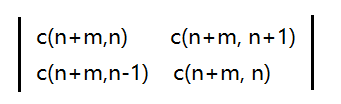然后可以直接写了，行列式就是，组合数直接得出每个的方案数 = c[n+m][n]*c[n+m][n] - c[n+m][n-1]*c[n+m][n+1];

code:

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define met(a, b) memset(a, b, sizeof(a))
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define bep(i, a, b) for(int i = a; i >= b; i--)
#define pb push_back
#define mp make_pair
#define debug cout << "KKK" << endl
#define ls num*2
#define rs num*2+1
#define re return 0
using namespace std;
const ll mod = 1e9 + 7;
const double PI = acos(-1);
const ll INF = 2e18+1;
const int inf = 1e9 + 15;
const double eps = 1e-7;
const int maxn = 1e6 + 5;
ll c[2005][1111];
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    c[0][0] = 1;
    rep(i, 1, 2000){
        c[i][0] = 1;
        rep(j, 1, min(i, 1005)){
            c[i][j] = (c[i-1][j] + c[i-1][j-1]) % mod;
        }
    }
    int n, m;
    while(cin >> n >> m){
        cout << ((c[n+m][n]*c[n+m][n])%mod - (c[n+m][n-1]*c[n+m][n+1])%mod + mod) % mod << endl;
    }
    re;
}