机器学习04-(决策树、集合算法:AdaBoost模型、BBDT、随机森林、分类模型:逻辑回归)
机器学习04
机器学习-04
集合算法
根据多个不同模型给出的预测结果,利用平均(回归)或者投票(分类)的方法,得出最终预测结果。
基于决策树的集合算法,就是按照某种规则,构建多棵彼此不同的决策树模型,分别给出针对未知样本的预测结果,最后通过平均或投票得到相对综合的结论。常用的集合模型包括Boosting类模型(AdaBoost、GBDT)与Bagging(自助聚合、随机森林)类模型。
AdaBoost模型(正向激励)
首先为样本矩阵中的样本随机分配初始权重,由此构建一棵带有权重的决策树,在由该决策树提供预测输出时,通过加权平均或者加权投票的方式产生预测值。将训练样本代入模型,预测其输出,对那些预测值与实际值不同的样本,提高其权重,由此形成第二棵决策树。重复以上过程,构建出不同权重的若干棵决策树。
正向激励相关API:
import sklearn.tree as st
import sklearn.ensemble as se
# model: 决策树模型(一颗)
model = st.DecisionTreeRegressor(max_depth=4)
# 自适应增强决策树回归模型
# n_estimators:构建400棵不同权重的决策树,训练模型
model = se.AdaBoostRegressor(model, n_estimators=400, random_state=7)
# 训练模型
model.fit(train_x, train_y)
# 测试模型
pred_test_y = model.predict(test_x)
案例:基于正向激励训练预测波士顿地区房屋价格的模型。
# 创建基于决策树的正向激励回归器模型
model = se.AdaBoostRegressor(
st.DecisionTreeRegressor(max_depth=4), n_estimators=400, random_state=7)
# 训练模型
model.fit(train_x, train_y)
# 测试模型
pred_test_y = model.predict(test_x)
print(sm.r2_score(test_y, pred_test_y))
特征重要性
作为决策树模型训练过程的副产品,根据划分子表时选择特征的顺序标志了该特征的重要程度,此即为该特征重要性指标。训练得到的模型对象提供了属性:feature_importances_来存储每个特征的重要性。
获取样本矩阵特征重要性属性:
model.fit(train_x, train_y)
fi = model.feature_importances_
案例:获取普通决策树与正向激励决策树训练的两个模型的特征重要性值,按照从大到小顺序输出绘图。
import matplotlib.pyplot as mp
model = st.DecisionTreeRegressor(max_depth=4)
model.fit(train_x, train_y)
# 决策树回归器给出的特征重要性
fi_dt = model.feature_importances_
model = se.AdaBoostRegressor(
st.DecisionTreeRegressor(max_depth=4), n_estimators=400, random_state=7)
model.fit(train_x, train_y)
# 基于决策树的正向激励回归器给出的特征重要性
fi_ab = model.feature_importances_
mp.figure('Feature Importance', facecolor='lightgray')
mp.subplot(211)
mp.title('Decision Tree', fontsize=16)
mp.ylabel('Importance', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(axis='y', linestyle=':')
sorted_indices = fi_dt.argsort()[::-1]
pos = np.arange(sorted_indices.size)
mp.bar(pos, fi_dt[sorted_indices], facecolor='deepskyblue', edgecolor='steelblue')
mp.xticks(pos, feature_names[sorted_indices], rotation=30)
mp.subplot(212)
mp.title('AdaBoost Decision Tree', fontsize=16)
mp.ylabel('Importance', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(axis='y', linestyle=':')
sorted_indices = fi_ab.argsort()[::-1]
pos = np.arange(sorted_indices.size)
mp.bar(pos, fi_ab[sorted_indices], facecolor='lightcoral', edgecolor='indianred')
mp.xticks(pos, feature_names[sorted_indices], rotation=30)
mp.tight_layout()
mp.show()
GBDT
GBDT(Gradient Boosting Decision Tree 梯度提升树)通过多轮迭代,每轮迭代产生一个弱分类器,每个分类器在上一轮分类器的残差**(残差在数理统计中是指实际观察值与估计值(拟合值)之间的差)**基础上进行训练。基于预测结果的残差设计损失函数。GBDT训练的过程即是求该损失函数最小值的过程。
案例:预测年龄
| 样本 | 消费金额 | 上网时长 | 年龄 |
|---|---|---|---|
| A | 1000 | 1 | 14 |
| B | 800 | 1.2 | 16 |
| C | 1200 | 0.9 | 24 |
| D | 1400 | 1.5 | 26 |
训练第一颗决策树:
总
样
本
{
(
金
额
<
=
1000
)
⇒
[
A
1000
1
14
B
800
1.2
16
]
(
金
额
>
1000
)
⇒
[
C
1200
1
24
D
1400
1.5
26
]
总样本\left\{ \begin{aligned} (金额<=1000) \quad \Rightarrow \quad \begin{bmatrix} A & 1000 & 1 & 14\\ B & 800 & 1.2 & 16\\ \end{bmatrix}\\ \\ (金额>1000) \quad \Rightarrow \quad \begin{bmatrix} C & 1200 & 1 & 24\\ D & 1400 & 1.5 & 26\\ \end{bmatrix}\\ \end{aligned} \right.
总样本⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧(金额<=1000)⇒[AB100080011.21416](金额>1000)⇒[CD1200140011.52426]
计算每个样本的真实结果与预测结果之差(残差):
| 样本 | 消费金额 | 上网时长 | 残差 |
|---|---|---|---|
| A | 1000 | 1 | -1 |
| B | 800 | 1.2 | 1 |
| C | 1200 | 0.9 | -1 |
| D | 1400 | 1.5 | 1 |
基于残差训练第二颗决策树:
总
样
本
{
(
时
长
<
=
1
)
⇒
[
A
1000
1
−
1
C
1200
1
−
1
]
(
时
长
>
1
)
⇒
[
B
800
1.2
1
D
1400
1.5
1
]
总样本\left\{ \begin{aligned} (时长<=1) \quad \Rightarrow \quad \begin{bmatrix} A & 1000 & 1 & -1\\ C & 1200 & 1 & -1\\ \end{bmatrix}\\ \\ (时长>1) \quad \Rightarrow \quad \begin{bmatrix} B & 800 & 1.2 & 1\\ D & 1400 & 1.5 & 1\\ \end{bmatrix}\\ \end{aligned} \right.
总样本⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧(时长<=1)⇒[AC1000120011−1−1](时长>1)⇒[BD80014001.21.511]
再次计算每个样本残差为0,再无优化空间,迭代结束。
预测过程:预测以下样本的年龄:
| 样本 | 消费金额 | 上网时长 | 年龄 |
|---|---|---|---|
| E | 1200 | 1.6 | ? |
将每颗决策树的预测结果相加:
25
+
1
=
26
25 + 1 = 26
25+1=26
import sklearn.tree as st
import sklearn.ensemble as se
# 自适应增强决策树回归模型
# n_estimators:构建400棵不同权重的决策树,训练模型
model = se.GridientBoostingRegressor(
max_depth=10, n_estimators=1000, min_samples_split=2)
# 训练模型
model.fit(train_x, train_y)
# 测试模型
pred_test_y = model.predict(test_x)
自助聚合
每次从总样本矩阵中以有放回抽样的方式随机抽取部分样本构建决策树,这样形成多棵包含不同训练样本的决策树,以削弱某些强势样本对模型预测结果的影响,提高模型的泛化特性。
随机森林
在自助聚合的基础上,每次构建决策树模型时,不仅随机选择部分样本,而且还随机选择部分特征,这样的集合算法,不仅规避了强势样本对预测结果的影响,而且也削弱了强势特征的影响,使模型的预测能力更加泛化。
随机森林相关API:
import sklearn.ensemble as se
# 随机森林回归模型 (属于集合算法的一种)
# max_depth:决策树最大深度10
# n_estimators:构建1000棵决策树,训练模型
# min_samples_split: 子表中最小样本数 若小于这个数字,则不再继续向下拆分
model = se.RandomForestRegressor(
max_depth=10, n_estimators=1000, min_samples_split=2)
案例:分析共享单车的需求,从而判断如何进行共享单车的投放。
import numpy as np
import sklearn.utils as su
import sklearn.ensemble as se
import sklearn.metrics as sm
import matplotlib.pyplot as mp
data = np.loadtxt('../data/bike_day.csv', unpack=False, dtype='U20', delimiter=',')
day_headers = data[0, 2:13]
x = np.array(data[1:, 2:13], dtype=float)
y = np.array(data[1:, -1], dtype=float)
x, y = su.shuffle(x, y, random_state=7)
print(x.shape, y.shape)
train_size = int(len(x) * 0.9)
train_x, test_x, train_y, test_y = \
x[:train_size], x[train_size:], y[:train_size], y[train_size:]
# 随机森林回归器
model = se.RandomForestRegressor( max_depth=10, n_estimators=1000, min_samples_split=2)
model.fit(train_x, train_y)
# 基于“天”数据集的特征重要性
fi_dy = model.feature_importances_
pred_test_y = model.predict(test_x)
print(sm.r2_score(test_y, pred_test_y))
data = np.loadtxt('../data/bike_hour.csv', unpack=False, dtype='U20', delimiter=',')
hour_headers = data[0, 2:13]
x = np.array(data[1:, 2:13], dtype=float)
y = np.array(data[1:, -1], dtype=float)
x, y = su.shuffle(x, y, random_state=7)
train_size = int(len(x) * 0.9)
train_x, test_x, train_y, test_y = \
x[:train_size], x[train_size:], \
y[:train_size], y[train_size:]
# 随机森林回归器
model = se.RandomForestRegressor(
max_depth=10, n_estimators=1000,
min_samples_split=2)
model.fit(train_x, train_y)
# 基于“小时”数据集的特征重要性
fi_hr = model.feature_importances_
pred_test_y = model.predict(test_x)
print(sm.r2_score(test_y, pred_test_y))
画图显示两组样本数据的特征重要性:
mp.figure('Bike', facecolor='lightgray')
mp.subplot(211)
mp.title('Day', fontsize=16)
mp.ylabel('Importance', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(axis='y', linestyle=':')
sorted_indices = fi_dy.argsort()[::-1]
pos = np.arange(sorted_indices.size)
mp.bar(pos, fi_dy[sorted_indices], facecolor='deepskyblue', edgecolor='steelblue')
mp.xticks(pos, day_headers[sorted_indices], rotation=30)
mp.subplot(212)
mp.title('Hour', fontsize=16)
mp.ylabel('Importance', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(axis='y', linestyle=':')
sorted_indices = fi_hr.argsort()[::-1]
pos = np.arange(sorted_indices.size)
mp.bar(pos, fi_hr[sorted_indices], facecolor='lightcoral', edgecolor='indianred')
mp.xticks(pos, hour_headers[sorted_indices], rotation=30)
mp.tight_layout()
mp.show()
分类模型
什么问题属于分类问题?
sklearn.datasets.load_iris() 鸢尾花数据集
逻辑回归
逻辑回归分类模型是一种基于回归思想实现分类业务的分类模型。
逻辑回归做二元分类时的核心思想为:
针对输出为{0, 1}的已知训练样本训练一个回归模型,使得训练样本的预测输出限制在(0, 1)的数值区间。该使原类别为0的样本的输出更接近于0,原类别为1的样本的输出更接近于1。这样就可以使用相同的回归模型来完成分类预测。
逻辑回归原理:
逻辑回归目标函数:
逻
辑
函
数
(
s
i
g
m
o
i
d
)
:
y
=
1
1
+
e
−
z
;
z
=
w
T
x
+
b
逻辑函数(sigmoid):y = \frac{1}{1+e^{-z}}; \quad z=w^Tx+b
逻辑函数(sigmoid):y=1+e−z1;z=wTx+b
该逻辑函数值域被限制在(0, 1)区间,当x>0,y>0.5;当x<0, y<0.5。可以把训练样本数据通过线性预测模型
z
z
z 代入逻辑函数,找到一组最优秀的模型参数使得原本属于1类别的样本输出趋近于1;原本属于0类别的样本输出趋近于0。即将预测函数的输出看做被划分为1类的概率,择概率大的类别作为预测结果。
逻辑回归相关API:
import sklearn.linear_model as lm
# 构建逻辑回归器
# solver:逻辑函数中指数的函数关系(liblinear为线型函数关系)
# C:参数代表正则强度,为了防止过拟合。正则越大拟合效果越小。
model = lm.LogisticRegression(solver='liblinear', C=正则强度)
model.fit(训练输入集,训练输出集)
result = model.predict(带预测输入集)
案例:基于逻辑回归器绘制网格化坐标颜色矩阵。
import numpy as np
import sklearn.linear_model as lm
import matplotlib.pyplot as mp
x = np.array([
[3, 1],
[2, 5],
[1, 8],
[6, 4],
[5, 2],
[3, 5],
[4, 7],
[4, -1]])
y = np.array([0, 1, 1, 0, 0, 1, 1, 0])`
# 逻辑分类器
model = lm.LogisticRegression(solver='liblinear', C=1)
model.fit(x, y)
l, r = x[:, 0].min() - 1, x[:, 0].max() + 1
b, t = x[:, 1].min() - 1, x[:, 1].max() + 1
n = 500
grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n))
samples = np.column_stack((grid_x.ravel(), grid_y.ravel()))
grid_z = model.predict(samples)
grid_z = grid_z.reshape(grid_x.shape)
mp.figure('Logistic Classification', facecolor='lightgray')
mp.title('Logistic Classification', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x, grid_y, grid_z, cmap='gray')
mp.scatter(x[:, 0], x[:, 1], c=y, cmap='brg', s=80)
mp.show()
多元分类
通过多个二元分类器解决多元分类问题。
| 特征1 | 特征2 | ==> | 所属类别 |
|---|---|---|---|
| 4 | 7 | ==> | A |
| 3.5 | 8 | ==> | A |
| 1.2 | 1.9 | ==> | B |
| 5.4 | 2.2 | ==> | C |
若拿到一组新的样本,可以基于二元逻辑分类训练出一个模型判断属于A类别的概率。再使用同样的方法训练出两个模型分别判断属于B、C类型的概率,最终选择概率最高的类别作为新样本的分类结果。
案例:基于逻辑分类模型的多元分类。
import numpy as np
import sklearn.linear_model as lm
import matplotlib.pyplot as mp
x = np.array([
[4, 7],
[3.5, 8],
[3.1, 6.2],
[0.5, 1],
[1, 2],
[1.2, 1.9],
[6, 2],
[5.7, 1.5],
[5.4, 2.2]])
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2])
# 逻辑分类器
model = lm.LogisticRegression(solver='liblinear', C=1000)
model.fit(x, y)
l, r = x[:, 0].min() - 1, x[:, 0].max() + 1
b, t = x[:, 1].min() - 1, x[:, 1].max() + 1
n = 500
grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n))
samples = np.column_stack((grid_x.ravel(), grid_y.ravel()))
grid_z = model.predict(samples)
print(grid_z)
grid_z = grid_z.reshape(grid_x.shape)
mp.figure('Logistic Classification', facecolor='lightgray')
mp.title('Logistic Classification', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x, grid_y, grid_z, cmap='gray')
mp.scatter(x[:, 0], x[:, 1], c=y, cmap='brg', s=80)
mp.show()
代码总结
波士顿房屋价格数据分析与房价预测
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as sd
import sklearn.utils as su
import pandas as pd
# 加载数据集
boston = sd.load_boston()
# print(boston.DESCR)
x, y, header = boston.data, boston.target, boston.feature_names
# 针对当前数据集,做简单的数据分析
data = pd.DataFrame(x, columns=header)
data['y'] = y
data.describe()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 |
| mean | 3.593761 | 11.363636 | 11.136779 | 0.069170 | 0.554695 | 6.284634 | 68.574901 | 3.795043 | 9.549407 | 408.237154 | 18.455534 | 356.674032 | 12.653063 | 22.532806 |
| std | 8.596783 | 23.322453 | 6.860353 | 0.253994 | 0.115878 | 0.702617 | 28.148861 | 2.105710 | 8.707259 | 168.537116 | 2.164946 | 91.294864 | 7.141062 | 9.197104 |
| min | 0.006320 | 0.000000 | 0.460000 | 0.000000 | 0.385000 | 3.561000 | 2.900000 | 1.129600 | 1.000000 | 187.000000 | 12.600000 | 0.320000 | 1.730000 | 5.000000 |
| 25% | 0.082045 | 0.000000 | 5.190000 | 0.000000 | 0.449000 | 5.885500 | 45.025000 | 2.100175 | 4.000000 | 279.000000 | 17.400000 | 375.377500 | 6.950000 | 17.025000 |
| 50% | 0.256510 | 0.000000 | 9.690000 | 0.000000 | 0.538000 | 6.208500 | 77.500000 | 3.207450 | 5.000000 | 330.000000 | 19.050000 | 391.440000 | 11.360000 | 21.200000 |
| 75% | 3.647423 | 12.500000 | 18.100000 | 0.000000 | 0.624000 | 6.623500 | 94.075000 | 5.188425 | 24.000000 | 666.000000 | 20.200000 | 396.225000 | 16.955000 | 25.000000 |
| max | 88.976200 | 100.000000 | 27.740000 | 1.000000 | 0.871000 | 8.780000 | 100.000000 | 12.126500 | 24.000000 | 711.000000 | 22.000000 | 396.900000 | 37.970000 | 50.000000 |
data.pivot_table(index='CHAS', values='y')
| y | |
|---|---|
| CHAS | |
| 0.0 | 22.093843 |
| 1.0 | 28.440000 |
data['DIS'].plot.box()
<matplotlib.axes._subplots.AxesSubplot at 0x2d7838dc5c0>
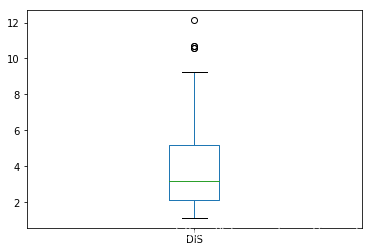
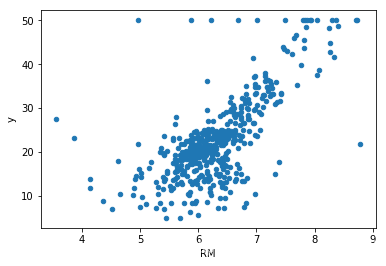
# 判断每个字段与房价之间的关系
data.plot.scatter(x='RM', y='y')
<matplotlib.axes._subplots.AxesSubplot at 0x2d78388b240>
训练回归模型,预测房屋价格
- 整理数据集(输入集、输出集)
- 打乱数据集,拆分测试集、训练集。
- 选择模型,使用训练集训练模型,用测试集测试。
# 整理数据集(输入集、输出集)
x, y = data.iloc[:, :-1], data['y']
# 打乱数据集。 su: sklearn.utils
# random_state:随机种子。 若两次随机操作使用的随机种子相同,则随机结果也相同。
x, y = su.shuffle(x, y, random_state=7)
# 拆分测试集、训练集。
train_size = int(len(x) * 0.9)
train_x, test_x, train_y, test_y = \
x[:train_size], x[train_size:], y[:train_size], y[train_size:]
train_x.shape, test_x.shape, train_y.shape, test_y.shape
((455, 13), (51, 13), (455,), (51,))
决策树回归
import sklearn.tree as st
import sklearn.metrics as sm
# 决策树回归模型,使用训练集训练模型,用测试集测试。
model = st.DecisionTreeRegressor(max_depth=4)
model.fit(train_x, train_y) # 针对训练集数据进行训练
pred_test_y = model.predict(test_x) # 针对测试集数据进行测试
print(sm.r2_score(test_y, pred_test_y))
print(sm.mean_absolute_error(test_y, pred_test_y))
# 输出单棵决策树的特征重要性指标
fi = model.feature_importances_
print(fi)
print(header)
0.678829897847864
2.923060066720631
[0.04992925 0. 0. 0. 0.02788393 0.62987544
0.00067595 0.0908006 0. 0. 0.00415868 0.
0.19667614]
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
import graphviz
dot_data = st.export_graphviz(model,out_file=None,feature_names= header)
graph = graphviz.Source(dot_data)
graph
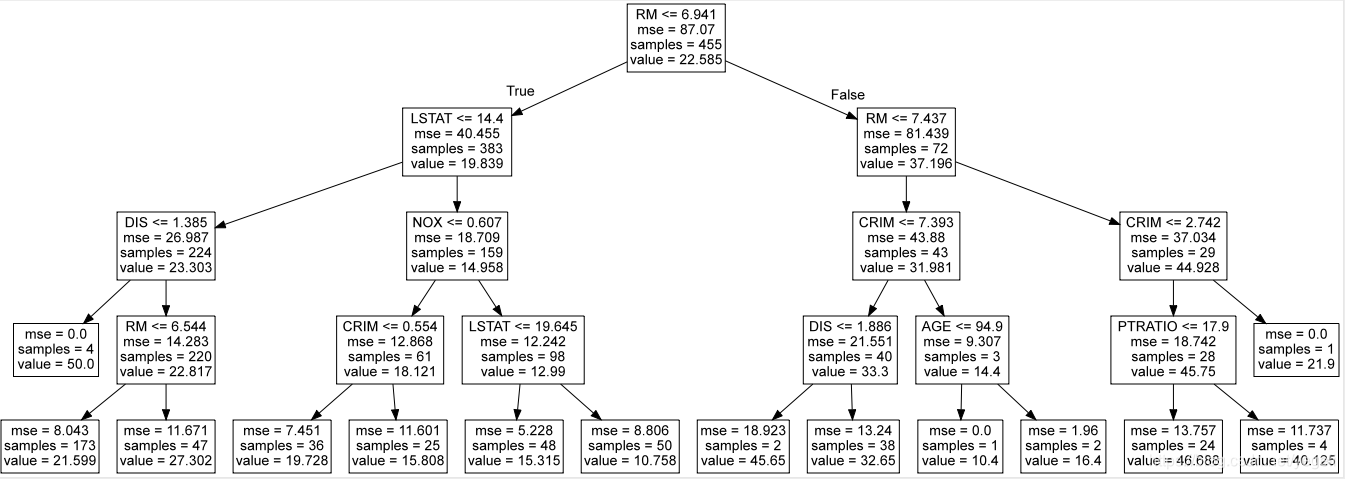
正向激励
import sklearn.ensemble as se
# AdaBoost回归模型,使用训练集训练模型,用测试集测试。
# 调整参数
# params1 = [6, 7]
# params2 = [50, 100, 150, 200]
# for p1 in params1:
# for p2 in params2:
# model = st.DecisionTreeRegressor(max_depth=p1)
# model = se.AdaBoostRegressor(model, n_estimators=p2, random_state=7)
# model.fit(train_x, train_y) # 针对训练集数据进行训练
# pred_test_y = model.predict(test_x) # 针对测试集数据进行测试
# print('max_depth:', p1, ' n_estimators:', p2)
# print(sm.r2_score(test_y, pred_test_y))
# print(sm.mean_absolute_error(test_y, pred_test_y))
model = st.DecisionTreeRegressor(max_depth=6)
model = se.AdaBoostRegressor(model, n_estimators=100, random_state=7)
model.fit(train_x, train_y) # 针对训练集数据进行训练
pred_test_y = model.predict(test_x) # 针对测试集数据进行测试
print(sm.r2_score(test_y, pred_test_y))
print(sm.mean_absolute_error(test_y, pred_test_y))
# 输出单棵决策树的特征重要性指标
fi = model.feature_importances_
print(fi)
print(header)
# 特征重要性可视化
s = pd.Series(fi, index=header)
s.sort_values().plot.barh()
0.8814458900728809
2.060418077972981
[0.03474378 0.00092137 0.00581656 0.00102895 0.03494231 0.23408824
0.01790326 0.10480302 0.00889913 0.02894075 0.03176375 0.01503917
0.48110971]
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
<matplotlib.axes._subplots.AxesSubplot at 0x2d786e57400>
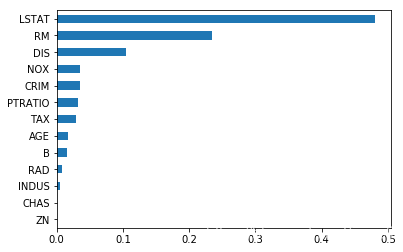
GBDT
model = se.GradientBoostingRegressor(
max_depth=6, n_estimators=1000, min_samples_split=15)
model.fit(train_x, train_y)
pred_test_y = model.predict(test_x)
print(sm.r2_score(test_y, pred_test_y))
print(sm.mean_absolute_error(test_y, pred_test_y))
0.9293816082262505
1.610908989775633
随机森林
model = se.RandomForestRegressor(
max_depth=10, n_estimators=1000, min_samples_split=4)
model.fit(train_x, train_y)
pred_test_y = model.predict(test_x)
print(sm.r2_score(test_y, pred_test_y))
print(sm.mean_absolute_error(test_y, pred_test_y))
0.8977117124659044
1.9161244706102394
案例:共享单车投放量分析与预测
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sklearn.preprocessing as sp
import sklearn.utils as su
import sklearn.linear_model as lm
import sklearn.tree as st
import sklearn.ensemble as se
import sklearn.metrics as sm
# 加载共享单车数据集,完成基本数据分析
data = pd.read_csv('../data/bike_day.csv')
# 特征工程,删除不必要的特征
data = data.drop(['instant', 'dteday', 'casual', 'registered'], axis=1)
data.describe()
| season | yr | mnth | holiday | weekday | workingday | weathersit | temp | atemp | hum | windspeed | cnt | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 731.000000 | 731.000000 | 731.000000 | 731.000000 | 731.000000 | 731.000000 | 731.000000 | 731.000000 | 731.000000 | 731.000000 | 731.000000 | 731.000000 |
| mean | 2.496580 | 0.500684 | 6.519836 | 0.028728 | 2.997264 | 0.683995 | 1.395349 | 0.495385 | 0.474354 | 0.627894 | 0.190486 | 4504.348837 |
| std | 1.110807 | 0.500342 | 3.451913 | 0.167155 | 2.004787 | 0.465233 | 0.544894 | 0.183051 | 0.162961 | 0.142429 | 0.077498 | 1937.211452 |
| min | 1.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.059130 | 0.079070 | 0.000000 | 0.022392 | 22.000000 |
| 25% | 2.000000 | 0.000000 | 4.000000 | 0.000000 | 1.000000 | 0.000000 | 1.000000 | 0.337083 | 0.337842 | 0.520000 | 0.134950 | 3152.000000 |
| 50% | 3.000000 | 1.000000 | 7.000000 | 0.000000 | 3.000000 | 1.000000 | 1.000000 | 0.498333 | 0.486733 | 0.626667 | 0.180975 | 4548.000000 |
| 75% | 3.000000 | 1.000000 | 10.000000 | 0.000000 | 5.000000 | 1.000000 | 2.000000 | 0.655417 | 0.608602 | 0.730209 | 0.233214 | 5956.000000 |
| max | 4.000000 | 1.000000 | 12.000000 | 1.000000 | 6.000000 | 1.000000 | 3.000000 | 0.861667 | 0.840896 | 0.972500 | 0.507463 | 8714.000000 |
# 离散型特征数值分析
data['weathersit'].value_counts()
1 463
2 247
3 21
Name: weathersit, dtype: int64
data.pivot_table(index='weathersit', values='cnt')
| cnt | |
|---|---|
| weathersit | |
| 1 | 4876.786177 |
| 2 | 4035.862348 |
| 3 | 1803.285714 |
data.pivot_table(index='workingday', values='cnt')
| cnt | |
|---|---|
| workingday | |
| 0 | 4330.168831 |
| 1 | 4584.820000 |
data.pivot_table(index='weekday', values='cnt')
| cnt | |
|---|---|
| weekday | |
| 0 | 4228.828571 |
| 1 | 4338.123810 |
| 2 | 4510.663462 |
| 3 | 4548.538462 |
| 4 | 4667.259615 |
| 5 | 4690.288462 |
| 6 | 4550.542857 |
# 连续型特征数值分析
data[['temp', 'atemp', 'hum', 'windspeed']].plot.box()
<matplotlib.axes._subplots.AxesSubplot at 0x2161e29dfd0>
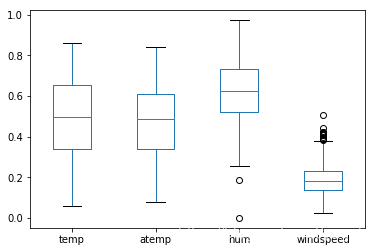
训练机器学习模型,预测共享单车使用量
# 1. 整理输入集x 与 输出集y
x, y = data.iloc[:, :-1], data['cnt']
x.shape, y.shape
# 2. 拆分测试集与训练集
x, y = su.shuffle(x, y, random_state=7)
train_size = int(len(x) * 0.9)
train_x, test_x, train_y, test_y = \
x[:train_size], x[train_size:], y[:train_size], y[train_size:]
# 3. 选择模型,训练模型
model = se.RandomForestRegressor(
max_depth=10, n_estimators=1000, min_samples_split=3)
model.fit(train_x, train_y)
# 预测
pred_train_y = model.predict(train_x)
pred_test_y = model.predict(test_x)
# 4. 评估模型
print('train r2 score:', sm.r2_score(train_y, pred_train_y))
print('test r2 score:', sm.r2_score(test_y, pred_test_y))
train r2 score: 0.9773682034502736
test r2 score: 0.891479300161597
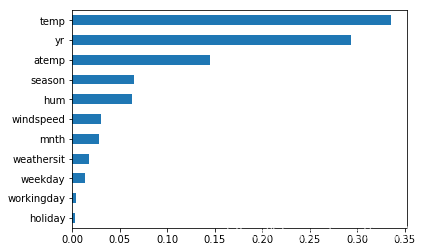
# 输出特征重要性
fi = model.feature_importances_
header = x.columns
s = pd.Series(fi, index=header)
s.sort_values().plot.barh()
<matplotlib.axes._subplots.AxesSubplot at 0x216204655c0>
以hour为单位的共享单车投放量预测
# 加载共享单车数据集,完成基本数据分析
data = pd.read_csv('../data/bike_hour.csv')
# 特征工程,删除不必要的特征
data = data.drop(['instant', 'dteday', 'casual', 'registered'], axis=1)
# 1. 整理输入集x 与 输出集y
x, y = data.iloc[:, :-1], data['cnt']
x.shape, y.shape
# 2. 拆分测试集与训练集
x, y = su.shuffle(x, y, random_state=7)
train_size = int(len(x) * 0.9)
train_x, test_x, train_y, test_y = \
x[:train_size], x[train_size:], y[:train_size], y[train_size:]
# 3. 选择模型,训练模型
model = se.RandomForestRegressor(
max_depth=10, n_estimators=1000, min_samples_split=3)
model.fit(train_x, train_y)
# 预测
pred_train_y = model.predict(train_x)
pred_test_y = model.predict(test_x)
# 4. 评估模型
print('train r2 score:', sm.r2_score(train_y, pred_train_y))
print('test r2 score:', sm.r2_score(test_y, pred_test_y))
train r2 score: 0.9420587049496375
test r2 score: 0.9185966492961931
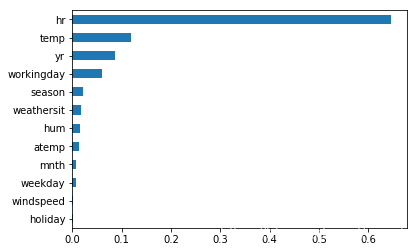
# 输出特征重要性
fi = model.feature_importances_
header = x.columns
s = pd.Series(fi, index=header)
s.sort_values().plot.barh()
<matplotlib.axes._subplots.AxesSubplot at 0x21620685550>
分类模型:鸢尾花数据集
import numpy as np
import pandas as pd
import sklearn.datasets as sd
# 加载鸢尾花数据集
iris = sd.load_iris()
# 简单封装并分析
data = pd.DataFrame(iris.data, columns=iris.feature_names)
data['target'] = iris.target
data.describe()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | |
|---|---|---|---|---|---|
| count | 150.000000 | 150.000000 | 150.000000 | 150.000000 | 150.000000 |
| mean | 5.843333 | 3.054000 | 3.758667 | 1.198667 | 1.000000 |
| std | 0.828066 | 0.433594 | 1.764420 | 0.763161 | 0.819232 |
| min | 4.300000 | 2.000000 | 1.000000 | 0.100000 | 0.000000 |
| 25% | 5.100000 | 2.800000 | 1.600000 | 0.300000 | 0.000000 |
| 50% | 5.800000 | 3.000000 | 4.350000 | 1.300000 | 1.000000 |
| 75% | 6.400000 | 3.300000 | 5.100000 | 1.800000 | 2.000000 |
| max | 7.900000 | 4.400000 | 6.900000 | 2.500000 | 2.000000 |
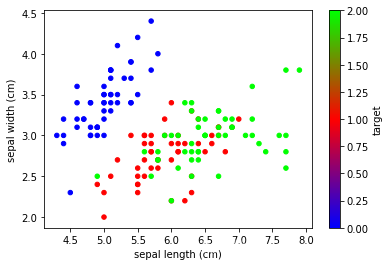
# 分析不同类别下鸢尾花其他属性特征的规律
data.pivot_table(index='target')
| petal length (cm) | petal width (cm) | sepal length (cm) | sepal width (cm) | |
|---|---|---|---|---|
| target | ||||
| 0 | 1.464 | 0.244 | 5.006 | 3.418 |
| 1 | 4.260 | 1.326 | 5.936 | 2.770 |
| 2 | 5.552 | 2.026 | 6.588 | 2.974 |
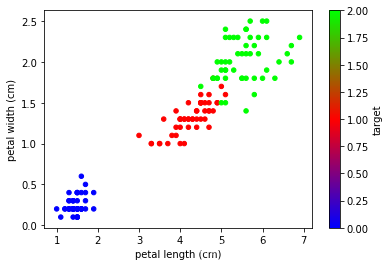
data.plot.scatter(x='sepal length (cm)', y='sepal width (cm)',
c='target', cmap='brg')
<matplotlib.axes._subplots.AxesSubplot at 0x17de30ff080>
data.plot.scatter(x='petal length (cm)', y='petal width (cm)',
c='target', cmap='brg')
<matplotlib.axes._subplots.AxesSubplot at 0x17de324ff28>
# 整理一组简单数据,训练逻辑回归模型,完成分类业务。
import sklearn.utils as su
import sklearn.linear_model as lm
sub_data = data.tail(150)
# 整理输入集与输出集
x, y = sub_data.iloc[:, :-1], sub_data['target']
# 拆分测试集与训练集
x, y = su.shuffle(x, y, random_state=7)
train_size = 70
train_x, test_x, train_y, test_y = \
x[:train_size], x[train_size:], y[:train_size], y[train_size:]
# 训练模型,并使用测试数据评估模型
model = lm.LogisticRegression()
model.fit(train_x, train_y)
pred_test_y = model.predict(test_x)
# 对于分类结果的评估:
(pred_test_y==test_y).sum() / test_y.size
0.975
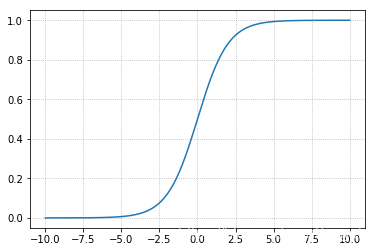
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 200)
y = 1 / (1 + np.exp(-x))
plt.grid(linestyle=':')
plt.plot(x, y)
[<matplotlib.lines.Line2D at 0x17de33d4358>]
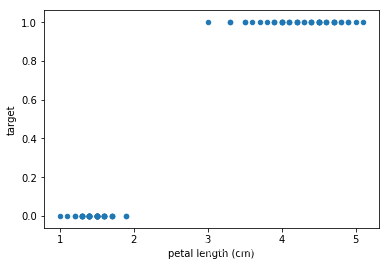
data[['petal length (cm)', 'target']].head(100).plot.scatter(x='petal length (cm)', y='target')
<matplotlib.axes._subplots.AxesSubplot at 0x17de33fd128>
机器学习04-(决策树、集合算法:AdaBoost模型、BBDT、随机森林、分类模型:逻辑回归)的更多相关文章
- 机器学习---三种线性算法的比较(线性回归,感知机,逻辑回归)(Machine Learning Linear Regression Perceptron Logistic Regression Comparison)
最小二乘线性回归,感知机,逻辑回归的比较: 最小二乘线性回归 Least Squares Linear Regression 感知机 Perceptron 二分类逻辑回归 Binary Logis ...
- 机器学习之决策树(ID3)算法与Python实现
机器学习之决策树(ID3)算法与Python实现 机器学习中,决策树是一个预测模型:他代表的是对象属性与对象值之间的一种映射关系.树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每 ...
- 机器学习算法与Python实践之(七)逻辑回归(Logistic Regression)
http://blog.csdn.net/zouxy09/article/details/20319673 机器学习算法与Python实践之(七)逻辑回归(Logistic Regression) z ...
- 机器学习之决策树_CART算法
目录 3.CART算法(classification and regression tree tree) 3.1 CART生成算法(回归树生成和分类树生成) 3.2 CART剪枝 决策树基本知识参考, ...
- 机器学习之路:python 集成分类器 随机森林分类RandomForestClassifier 梯度提升决策树分类GradientBoostingClassifier 预测泰坦尼克号幸存者
python3 学习使用随机森林分类器 梯度提升决策树分类 的api,并将他们和单一决策树预测结果做出对比 附上我的git,欢迎大家来参考我其他分类器的代码: https://github.com/l ...
- 机器学习算法整理(二)梯度下降求解逻辑回归 python实现
逻辑回归(Logistic regression) 以下均为自己看视频做的笔记,自用,侵删! 还参考了:http://www.ai-start.com/ml2014/ 用梯度下降求解逻辑回归 Logi ...
- 机器学习算法笔记1_2:分类和逻辑回归(Classification and Logistic regression)
形式: 採用sigmoid函数: g(z)=11+e−z 其导数为g′(z)=(1−g(z))g(z) 如果: 即: 若有m个样本,则似然函数形式是: 对数形式: 採用梯度上升法求其最大值 求导: 更 ...
- 决策树模型组合之(在线)随机森林与GBDT
前言: 决策树这种算法有着很多良好的特性,比如说训练时间复杂度较低,预测的过程比较快速,模型容易展示(容易将得到的决策树做成图片展示出来)等.但是同时, 单决策树又有一些不好的地方,比如说容易over ...
- 斯坦福CS229机器学习课程笔记 part2:分类和逻辑回归 Classificatiion and logistic regression
Logistic Regression 逻辑回归 1.模型 逻辑回归解决的是分类问题,并且是二元分类问题(binary classification),y只有0,1两个取值.对于分类问题使用线性回归不 ...
- 机器学习实战基础(三十七):随机森林 (四)之 RandomForestRegressor 重要参数,属性与接口
RandomForestRegressor class sklearn.ensemble.RandomForestRegressor (n_estimators=’warn’, criterion=’ ...
随机推荐
- Laravel安装第一步:Windows 10 上laravel下载与安装需要注意。
1.下载了laravel,查看composer.json文件,搞清楚它需要的PHP版本 2.不要用 composer install !!! 用 composer -vvv install 这样 ...
- python求列表中某个值第一次出现的位置
x=[2,1,1] print(x.index(1)) 结果为1
- CH573 CH582 CH579蓝牙从机(peripheral)例程讲解三(蓝牙服务修改)
修改服务需要对蓝牙比较熟悉的工程师去完成,否则在例程功能满足自己需求时,不建议修改,很容易改错,下面就简单介绍下如何在别的char添加一个nofify属性. step1: 给Simple Profil ...
- Apache Ranger系列七:Hive 和 Spark 执行过程中的文件路径配置
背景:在使用Ranger鉴权的过程中,要求必须开启impersonation功能(即执行用户与提交用户保持一致,而不是统一代理的hive/spark).但是在执行的过程中,会需要在hdfs存储临时的文 ...
- Executors.newScheduledThreadPool()定时任务线程池
定时任务线程池是由 Timer 进化而来 jdk中的计划任务 Timer 工具类提供了以计时器或计划任务的功能来实现按指定时间或时间间隔执行任务,但由于 Timer 工具类并不是以池 pool ,而是 ...
- P2962 [USACO09NOV]Lights G(Meet In The Middle)
[USACO09NOV]Lights G 题目描述 给出一张n个点n条边的无向图,每个点的初始状态都为0. 你可以操作任意一个点,操作结束后该点以及所有与该点相邻的点的状态都会改变,由0变成1或由1变 ...
- Switch问题
package com.company;public class Main { public static void main(String[] args) { Income[] incomes = ...
- Keil 报错解决方法:Cannot link object xxx.o as its attributes are incompatile with the image attributes
链接其他人的lib库时报错:Cannot link object xxx.o as its attributes are incompatile with the image attributes 解 ...
- 一篇博客带你学会MyBatis
概念 MyBatis是一款持久层框架,用于简化JDBC操作(JavaEE三层架构:表现层(用来做页面的代码),业务层(业务逻辑代码),持久层(对数据库操作的代码))(框架就是一个半成品软件,是一套可重 ...
- 痞子衡嵌入式:内存读写正确性压力测试程序(memtester)
大家好,我是痞子衡,是正经搞技术的痞子.今天痞子衡给大家介绍的是内存读写正确性压力测试程序memtester. 在嵌入式系统中,内存(RAM)的重要性不言而喻,系统性能及稳定性都与内存息息相关.关于内 ...
