OpenCASCADE解非线性方程组

eryar@163.com

Abstract. 在科学技术领域里常常提出求解非线性方程组的问题，例如，用非线性函数拟合实验数据问题、非线性网络问题、几何上的曲线曲面求交问题等。OpenCASCADE中有关于非线性方程组定义的类及其求解类，本文主要介绍如何在OpenCASCADE中定义非线性方程组，及对其进行求解。

Key Words. Function Set, Function Set Root, Newton Raphson Algorithm

1.Introduction

在科学技术领域里常常提出求解非线性方程组的问题，例如，用非线性函数拟合实验数据问题、非线性网络问题等。在几何造型中很多问题也可以利用非线性方程组来解决。如曲线的光顺，曲线求交、曲面求交、Blend造型问题等。

OpenCASCADE提供了非线性方程组的类math_FunctionSet，可以先从类图上来看看有哪些算法使用了这个类：

图1 曲线光顺包FaireCurve

图2 Blending Surface between two surfaces

感兴趣的同学可以自己打开OpenCASCADE的类索引文件查看。可以看到很多算法涉及到方程组的求解问题。本文主要介绍如何定义非线性方程组及对其进行求解。理解这些套路后，对math_FunctionSet相关的派生类及其用用途就会有个清晰的认识，便于对源码的理解。

2.Function Set Definition

设有非线性方程组

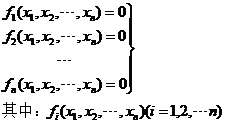
为实变量的非线方程函数。引入向量形式表示，引进记号：

于是非线性方程组可以简单记作：F(x)=0。我们的问题是寻求X使F(X)=0，这个X就是非线性方程组的解。

OpenCASCADE中使用类math_FunctionSet来表示方程组，这是个抽象类，定义了如下纯虚函数：

l NbVariables()：变量的个数，即末知量的个数；

l NbEquations()：方程的个数，即方程组中有几个方程；

l Value(const math_Vector&X, math_Vector& F)：方程组的值，即代入变量每个方程的值；

3.Function Set Root Algorithm

解非线性方程组的牛顿法和解方程式的思路一样，要求方程有一阶导数。而非线性方程组即是要求有偏导数。由fi(x)偏导数作成的矩阵记为J(x)或F’(x)，称为F(x)的Jacobi矩阵：

求解非线性方程组的牛顿法为：

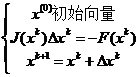
其中x^k为方程线的近似解向量。

OpenCASCADE中也提供了非线性方程组的求解类，如：math_FunctionSetRoot，math_NewtonFunctionSetRoot。而使用这些类的输入都是要求具有一阶偏导数的线性方程组的定义math_FunctionSetWithDerivaties。这个类定义了具有一阶偏导数的非线性方程组，其纯虚函数除了前面说明的几个以外，还增加了如下两个：

l Derivatives(const math_Vector& X, math_Matrix& D)：一阶偏导数值，即计算Jacobi矩阵；

l Values(const math_Vector& X, math_Vector& F, math_Matrix& D)：计算方程的值及一阶偏导数矩阵Jacobi矩阵。

4.Code Example

下面给出一个具体的例子来说明这些类的用法。设有非线性方程组：

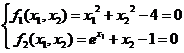
从几何上看其解就是圆心在原点，半径为2的圆与曲线的交点：

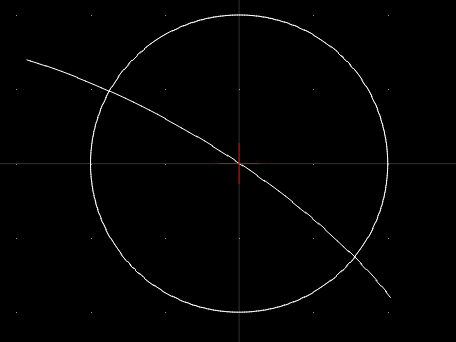
图3 圆与曲线求交

下面我们使用OpenCASCADE来对上述问题进行求解。首先定义这个非线性方程组：

#include <math_FunctionSet.hxx>

#include <math_FunctionSetWithDerivatives.hxx>

#include <math_FunctionSetRoot.hxx>

#pragma comment(lib, "TKernel.lib")

#pragma comment(lib, "TKMath.lib")

class MyFunctionSet : public math_FunctionSetWithDerivatives

{

public:

    virtual Standard_Integer NbVariables() const

    {

        return ;

    }

    virtual Standard_Integer NbEquations() const

    {

        return ;

    }

    virtual Standard_Boolean Value(const math_Vector& X, math_Vector& F)

    {

        F() = X() * X() + X() * X() - 4.0;

        F() = Pow(M_E, X()) + X() - 1.0;

        return Standard_True;

    }

    virtual Standard_Boolean Derivatives(const math_Vector& X, math_Matrix& D)

    {

        // matrix D is Jacobi matrix.

        D(, ) = 2.0 * X();

        D(, ) = 2.0 * X();

        D(, ) = Pow(M_E, X());

        D(, ) = 1.0;

        return Standard_True;

    }

    virtual Standard_Boolean Values(const math_Vector& X, math_Vector& F, math_Matrix& D)

    {

        Value(X, F);

        Derivatives(X, D);

        return Standard_True;

    }

private:

};

void test()

{

    MyFunctionSet aFunctionSet;

    math_FunctionSetRoot aSolver(aFunctionSet);

    math_Vector aStartingPoint(, );

    // 1. (1.0, 1.0)

    aStartingPoint() = 1.0;

    aStartingPoint() = 1.0;

    aSolver.Perform(aFunctionSet, aStartingPoint);

    if (aSolver.IsDone())

    {

        aSolver.Dump(std::cout);

    }

    // 2. (1.0, -1.0)

    aStartingPoint() = 1.0;

    aStartingPoint() = -1.0;

    aSolver.Perform(aFunctionSet, aStartingPoint);

    if (aSolver.IsDone())

    {

        aSolver.Dump(std::cout);

    }

}

int main(int argc, char* argv[])

{

    test();

    return ;

}

上述代码先定义了带有一阶偏导数的非线性方程组类：MyFunctionSet，因为有两个变量及两个方程，再分别实现计算方程值及偏导数的虚函数。

然后使用类math_FunctionSetRoot来对方程组进行求解，求解的结果如下图所示：

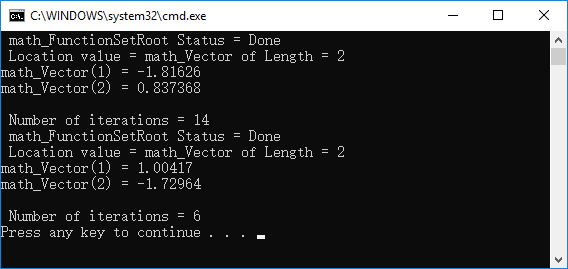
图4 非线性方程组求解结果

由图3可知，两个曲线相交有两个交点，但是使用类math_FunctionSetRoot一次只能计算一个解。从图4的计算结果还可以看出，初值的选择对解的影响很大，既影响计算结果，也影响迭代次数。

5.Conclusion

综上所述，OpenCASCADE的math工具箱中提供了方程组的定义、求解功能。其中对非线性方程组求解使用的是Newton迭代法，所以要求方程组必须实现计算一阶偏导数的虚函数，即计算Jacobi矩阵。

从OpenCASCADE类图中可以看出，方程组定义类用在了很多地方，所以理解上述对方程组的定义及解的用法，对其他使用这个派生类的地方更容易其源码。

6.References

同济大学数学教研室. 高等数学第四版. 高等教育出版社. 2004
易大义, 沈云宝, 李有法. 计算方法. 浙江大学出版社. 2002