[HAOI2009]毛毛虫（树形dp）

[HAOI2009]毛毛虫

题目描述

对于一棵树，我们可以将某条链和与该链相连的边抽出来，看上去就象成一个毛毛虫，点数越多，毛毛虫就越大。例如下图左边的树（图 1 ）抽出一部分就变成了右边的一个毛毛虫了（图 2 ）。

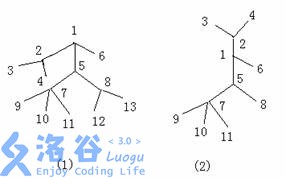
输入输出格式

输入格式：

在文本文件 worm.in 中第一行两个整数 N ， M ，分别表示树中结点个数和树的边数。

接下来 M 行，每行两个整数 a, b 表示点 a 和点 b 有边连接（ a, b ≤ N ）。你可以假定没有一对相同的 (a, b) 会出现一次以上。

输出格式：

在文本文件 worm.out 中写入一个整数 , 表示最大的毛毛虫的大小。

输入输出样例

输入样例#1： 复制

13 12

1 2

1 5

1 6

3 2

4 2

5 7

5 8

7 9

7 10

7 11

8 12

8 13

输出样例#1： 复制

11

说明

40% 的数据， N ≤ 50000

100% 的数据， N ≤ 300000

题解

我真傻，真的。

我一开始以为以1为根节点。

然后找两条分链加加起来就好了。

测一下60分，以为是对的。

于是。。。。6点到10点，没有调出来，生无可恋。

最后还是看题解了。我真菜

我怎么就没想到要把每一个点作为一次根呢

然后因为是相连的点换根。所以子树的变化就是原根少一个点的子树，那个点的子树加上原根。

dp判断一下当前f[i]表示以i为根的最大长度。

然后毛毛虫可以是拼起来的。也就是说要记录最长和次长链。

end.

代码

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
using namespace std;
const int N=300005;
struct node{
    int nex,to;
}e[N<<1];
int size[N],n,m,num,head[N];
int f[N],ans,pre[N];
void add(int from,int to){
    num++;
    e[num].to=to;
    e[num].nex=head[from];
    head[from]=num;
}

int read(){
    int x=0,w=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*w;
}

void dfs(int x,int fa){
    size[x]=1;//int sum=0;
    for(int i=head[x];i;i=e[i].nex){
        int v=e[i].to;
        if(v==fa)continue;
        size[x]++;dfs(v,x);
    }
}

void dfs2(int x,int fa){
    int max1=0,max2=0;
    for(int i=head[x];i;i=e[i].nex){
        int v=e[i].to;
        if(v==fa)continue;
        dfs2(v,x);
        if(f[v]>max1){
            max2=max1;max1=f[v];
        }
        else if(f[v]>max2)max2=f[v];
        f[x]=max(f[x],f[v]+size[x]-1);
    }
    ans=max(ans,max1+max2-1+size[x]);
}

int main(){
    n=read();m=read();
    for(int i=1;i<=m;i++){
        int x=read(),y=read();
        add(x,y);add(y,x);
        size[x]++;size[y]++;
    }
    for(int i=1;i<=n;i++)f[i]=1;
    dfs2(1,0);
    printf("%d\n",ans);
    return 0;
}