Sum of Medians

Sum of Medians

time limit per test

3 seconds

memory limit per test

256 megabytes

In one well-known algorithm of finding the k-th order statistics we should divide all elements into groups of five consecutive elements and find the median of each five. A median is called the middle element of a sorted array (it's the third largest element for a group of five). To increase the algorithm's performance speed on a modern video card, you should be able to find a sum of medians in each five of the array.

A sum of medians of a sorted k-element set S = {a1, a2, ..., ak}, where a1 < a2 < a3 < ... < ak, will be understood by as

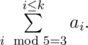
The 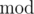 operator stands for taking the remainder, that is  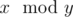stands for the remainder of dividing x by y.

To organize exercise testing quickly calculating the sum of medians for a changing set was needed.

Input

The first line contains number n (1 ≤ n ≤ 105), the number of operations performed.

Then each of n lines contains the description of one of the three operations:

• add x — add the element x to the set;
• del x — delete the element x from the set;
• sum — find the sum of medians of the set.

For any add x operation it is true that the element x is not included in the set directly before the operation.

For any del x operation it is true that the element x is included in the set directly before the operation.

All the numbers in the input are positive integers, not exceeding 109.

Output

For each operation sum print on the single line the sum of medians of the current set. If the set is empty, print 0.

Please, do not use the %lld specificator to read or write 64-bit integers in C++. It is preferred to use the cin, cout streams (also you may use the %I64d specificator).

Examples

input

6
add 4
add 5
add 1
add 2
add 3
sum

output

3

input

14
add 1
add 7
add 2
add 5
sum
add 6
add 8
add 9
add 3
add 4
add 10
sum
del 1
sum

output

5
11
13
分析：单点修改+区间查询下标i%5=3的值的和；
　　　暴力修改查询肯定慢了，所以考虑线段树；
　　　怎么查询i%5=3的和呢？这是难点；
　　　假设ret[rt][i]代表rt区间下标%5=i的和，sum[rt]代表rt区间的个数；
　　　考虑到了rt节点，ret[rt][i](rt区间内下标%5=i的和)显然可以加上ret[lson][i]，那么rson呢？
　　　这个可以推一推，结论是加上ret[rson][(i-sum[lson]%5+5)%5];
　　　所以线段树单点更新即可；
代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <bitset>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define mod 1000000007
#define inf 0x3f3f3f3f
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
#define pii pair<int,int>
#define sys system("pause")
const int maxn=1e5+;
const int N=1e3+;
using namespace std;
int id(int l,int r){return l+r|l!=r;}
ll gcd(ll p,ll q){return q==?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=;while(q){if(q&)f=f*p;p=p*p;q>>=;}return f;}
int n,m,k,t,sum[maxn<<],a[maxn],b[maxn],c[maxn],cnt;
ll ret[maxn<<][];
char op[];
void upd(int x,int y,int pos,int l,int r,int rt)
{
    int i;
    if(l==r)
    {
        sum[rt]+=x;
        ret[rt][]+=y;
        return;
    }
    int mid=l+r>>;
    if(pos<=mid)upd(x,y,pos,l,mid,id(l,mid));
    else upd(x,y,pos,mid+,r,id(mid+,r));
    rep(i,,)ret[rt][i]=ret[id(l,mid)][i]+ret[id(mid+,r)][(i-sum[id(l,mid)]%+)%];
    sum[rt]=sum[id(l,mid)]+sum[id(mid+,r)];
}
int main()
{
    int i,j;
    scanf("%d",&n);
    rep(i,,n)
    {
        scanf("%s",op);
        if(op[]=='s')a[i]=;
        else if(op[]=='d')scanf("%d",&b[i]),a[i]=;
        else scanf("%d",&b[i]),a[i]=,c[++cnt]=b[i];
    }
    sort(c+,c+cnt+);
    cnt=unique(c+,c+cnt+)-c-;
    rep(i,,n)
    {
        if(a[i]==)
        {
            upd(,b[i],lower_bound(c+,c+cnt+,b[i])-c,,cnt,id(,cnt));
        }
        else if(a[i]==)
        {
            upd(-,-b[i],lower_bound(c+,c+cnt+,b[i])-c,,cnt,id(,cnt));
        }
        else printf("%lld\n",ret[id(,cnt)][]);
    }
    return ;
}