18/9/22NOIP模拟考

　　　　　　　　18/9/22NOIP模拟考

其实本来是有多组数据的，出题人忘记在题面上加了   斜眼笑

期望得分：100；实际得分：100

由于种种原因，拿到题的时候已经过去了0.5h+。。。

然后因为这道题数据范围比较大，所以。。就想到了找规律

没想到居然A了  开心

这道题一共出现了三种做法：

1.出题人的std：据说是旋转坐标系什么鬼的，没听说过。。。

2.某人：从一个点做一个斜率为±1的一次函数，然后。。。如图

3.大部分人（包括我）：分别求出两点横纵坐标之差的绝对值，然后取max，完事

4.极少部分人：模拟 or 暴力？

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
using namespace std;
typedef long long LL;
LL n, s, t, c, f;

int main() {
    freopen("grid.in","r",stdin);
    freopen("grid.out","w",stdout);
    scanf("%I64d%I64d%I64d%I64d%I64d", &n, &s, &t, &c, &f);
    LL a = abs(s - c), b = abs(t - f);
    cout << max(a, b) << '\n';
    fclose(stdin); fclose(stdout);
    return ;
}

极其简短的我的代码 qwq

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cctype>
#include<cmath>
#include<set>
#include<map>
#include<queue>
#include<vector>
#include<cassert>
using namespace std;
typedef long long LL;

inline int read() {
    int x = , f = ; char ch = getchar(); for (; !isdigit(ch); ch=getchar()) if (ch=='-') f = -;
    for (; isdigit(ch); ch=getchar()) x = x *  + ch - ''; return x * f;
}

LL dx[] = {, , , -};
LL dy[] = {, -, , };

LL getdis(LL a,LL b,LL c,LL d,int flag) {
    if (flag) { // black
        a = (a - ) / , b = (b - ) / , c = (c - ) / , d = (d - ) / ;
        return abs(a - c) + abs(b - d);
    }
    else { // white
        a /= , b /= , c /= , d /= ;
        return abs(a - c) + abs(b - d);
    }
}
void getxy(LL a,LL b,LL &t1,LL &t2) {
    t1 = a + b,t2 = b - a;
}
int main() {

    freopen("grid.in","r",stdin);
    freopen("grid.out","w",stdout);

    LL Case,n, a, b, c, d, t1, t2, t3, t4, t5, t6;
//    cin >> Case;
//    while (Case--) {

        cin >> n >> a >> b >> c >> d;

        assert(a <= n);
        assert(b <= n);
        assert(c <= n);
        assert(d <= n);

        t1 = a + b, t2 = b - a;
        t3 = c + d, t4 = d - c;

        int f1, f2;
        if ((t1 & ) && (t2 & )) f1 = ;
        else f1 = ;
        if ((t3 & ) && (t4 & )) f2 = ;
        else f2 = ;

        LL ans = 1e18;
        if (f1 == f2) ans = getdis(t1, t2, t3, t4, f1);
        else {
            for (int i=; i<; ++i) {
                LL x = a + dx[i], y = b + dy[i];
                if (x >=  && x <=n && y >=  && y <= n) {
                    getxy(x, y, t5, t6);
                    ans = min(ans, getdis(t3, t4, t5, t6, f2) + );
                }
            }
            for (int i=; i<; ++i) {
                LL x = c + dx[i], y = d + dy[i];
                if (x >=  && x <=n && y >=  && y <= n) {
                    getxy(x, y, t5, t6);
                    ans = min(ans, getdis(t1, t2, t5, t6, f1) + );
                }
            }
        }
        cout << ans << "\n";
//    }
    return ;
}

std

期望得分：0；实际得分：0

其实还是希望有些分的，然而暴力没有调出来。。。

然后就gg了 qwq

正解：如果写了dfs的话，可以看出：我们只要知道上次填的串多长，就可以知道上次使用的字符串。而且对每个位置只需要知道它上次填2或3时是否可行。

$f[i][2/3]$表示当前到$i$，以$i$开头，长度为2/3的的后缀串是否可行。可以转移就记录答案。

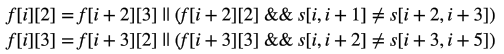
如果type ≠ 0，则不需要判断后缀是否相同

为了方便，可以把串反过来

复杂度：O(n)

#include <cstdio>
#include <cstring>
#include <algorithm>
#define pc putchar
const int N=;

bool f[N][]/*0:2 1:3*/,ok2[][],ok3[][][];
char s[N];

void Work(const int type) {
    memset(f,,sizeof f);
    memset(ok2,,sizeof ok2), memset(ok3,,sizeof ok3);

    scanf("%s",s+);
    int n=strlen(s+);
    std::reverse(s+,s++n);

    int tot=; n-=;
    if(n>=) f[][]=, ++tot, ok2[s[]-'a'][s[]-'a']=;
    if(n>=) f[][]=, ++tot, ok3[s[]-'a'][s[]-'a'][s[]-'a']=;

    for(int i=; i<=n; ++i) {
        int a=s[i]-'a', b=s[i-]-'a', c=s[i-]-'a';
        if(f[i-][]||(f[i-][]&&(type||s[i]!=s[i-]||s[i-]!=s[i-]))) {
            f[i][]=;
            if(!ok2[a][b]) ++tot, ok2[a][b]=;
        }
        if(f[i-][]||(f[i-][]&&(type||s[i]!=s[i-]||s[i-]!=s[i-]||s[i-]!=s[i-])))//i>=6
        {
            f[i][]=;
            if(!ok3[a][b][c]) ++tot, ok3[a][b][c]=;
        }
    }
    printf("%d\n",tot);
    for(int i=; i<&&tot; ++i) {
        for(int j=; j<; ++j) {
            if(ok2[i][j]) --tot,pc(i+'a'),pc(j+'a'),pc('\n');
            for(int k=; k<; ++k)
                if(ok3[i][j][k]) --tot,pc(i+'a'),pc(j+'a'),pc(k+'a'),pc('\n');
        }
    }
}

int main() {
    freopen("ling.in","r",stdin);
    freopen("ling.out","w",stdout);

    int T,type;
    for(scanf("%d%d",&T,&type); T--; Work(type));
    return ;
}

std

一看要求期望。。。一脸不可做。。。

整场考试也就瞄了几眼，一点想做的念头都没有。。。

蒻的一批。。。

事实证明，真心难啊 qwq

#include <cstdio>
#include <cctype>
#include <assert.h>
#include <algorithm>
#define gc() getchar()
const int N=5e5+;

int n,sz[N],fa[N],q[N],H[N],Enum,to[N],nxt[N];
double pw[N];//2^{-i}

inline int read() {
    int now=;register char c=gc();
    for(;!isdigit(c);c=gc());
    for(;isdigit(c);now=now*+c-'',c=gc());
    return now;
}
inline void AddEdge(int u,int v) {
    fa[v]=u, ++sz[u], ++sz[fa[u]];
    to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum;
}
double Calc(int x) {
    if(!sz[x]) return ;//sz:子树内点数
    int t=;//t:子节点数
    for(int i=H[x]; i; i=nxt[i]) q[t++]=to[i];
    if(t==sz[x])//D=2
        return -pw[t];
    else     {
        double ans=;
        for(int s=; s<<<t; ++s) {
            int tot=;
            for(int i=; i<t; ++i)
                if(s>>i&)
                    for(int j=H[q[i]]; j; j=nxt[j])
                        assert(!H[to[j]]), ++tot;
            ans+=pw[t]*(pw[tot]*+(-pw[tot])*);
        }
        return ans;
    }
}
void Subtask3(int Q) {
    static int dep[N];
    int H=; dep[]=;
    while(Q--) {
        int opt=read(),x=read();
        if(opt==) dep[++n]=++H;
        else {
            int h=H-dep[x];
            double ans=h*pw[h];
            for(int i=; i<h; ++i) ans+=i*pw[i+];
            printf("%.10lf\n",ans);
        }
    }
}

int main() {
    freopen("threebody.in","r",stdin);
    freopen("threebody.out","w",stdout);

    n=;
    int T=read(), Q=read(); pw[]=;
    for(int i=; i<=Q; ++i) pw[i]=pw[i-]*0.5;

    if(T==) {Subtask3(Q); return ;}

    while(Q--) {
        int opt=read(),x=read();
        if(opt==) AddEdge(x,++n);
        else if(T==) printf("%.10lf\n",-pw[sz[x]]);//Subtask2
        else printf("%.10lf\n",Calc(x));//Subtask1
    }
    return ;
}

subtask1.2.3.

#include <cstdio>
#include <cctype>
#include <assert.h>
#include <algorithm>
#define gc() getchar()
#define MAX_H 60
const int N=5e5+;

int n,fa[N];
double f[N][MAX_H];

inline int read() {
    int now=;register char c=gc();
    for(;!isdigit(c);c=gc());
    for(;isdigit(c);now=now*+c-'',c=gc());
    return now;
}

int main() {
    freopen("threebody.in","r",stdin);
    freopen("threebody.out","w",stdout);

    n=;
    for(int i=; i<MAX_H; ++i) f[][i]=;
    for(int T=read(), Q=read(); Q--; ) {
        int opt=read(),x=read();
        if(opt==) {
            fa[++n]=x;
            for(int i=; i<MAX_H; ++i) f[n][i]=;
            double tmp1=f[x][],tmp2;
            f[x][]*=0.5;
            for(int Fa=fa[x],i=; Fa&&i<MAX_H; Fa=fa[x=Fa],++i) {
                tmp2=f[Fa][i];
                f[Fa][i] /= 0.5 + 0.5*tmp1;
                f[Fa][i] *= 0.5 + 0.5*f[x][i-];
                tmp1=tmp2;
            }
        }
        else {
            double ans=; assert(x<=n);
            for(int i=; i<MAX_H; ++i) ans+=(f[x][i]-f[x][i-])*i;
            printf("%.10lf\n",ans);
        }
    }
    return ;
}

正解