HMM隐马尔可夫模型（词语粘合）

HMM用于自然语言处理（NLP）中文分词，是用来描述一个含有隐含未知参数的马尔可夫过程，其目的是希望通过求解这些隐含的参数来进行实体识别，说简单些也就是起到词语粘合的作用。

HMM隐马尔可夫模型包括：

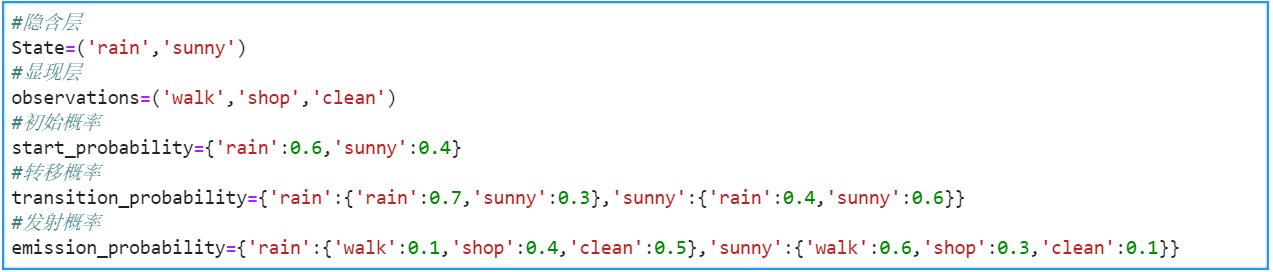
　　OBS 显现层（observations）

　　States 隐含层

　　Start_p 初始概率 P(a)

　　Trans_p 转移概率 P(b|a)

　　Emit_p 发射概率

例题：小黑每天根据天气【下雨、晴天】决定当天的活动【散步、购物、清理房间】，她有在朋友圈里发了一条信息“我前天在公园散步，昨天购物，今天清理房间了”，如何根据发的信息推断这三天的天气？

第一天：

【第一天】【散步】=【初始概率，下雨】*【发射概率，散步】=0.6*0.1=0.06
【第一天】【散步】=【初始概率，晴天】*【发射概率，散步】=0.4*0.6=0.24
　　因为0.24>0.06，第一天可能是晴天

第二天：

【第二天】【购物】=【第一天散步，初始概率，下雨】*【转移概率，下雨】*【发射概率，购物】=0.06*0.7*0.4=0.0168

【第二天】【购物】=【第一天散步，初始概率，下雨】*【转移概率，晴天】*【发射概率，购物】=0.06*0.3*0.3=0.0054

【第二天】【购物】=【第一天散步，初始概率，晴天】*【转移概率，下雨】*【发射概率，购物】=0.24*0.4*0.4=0.0384

【第二天】【购物】=【第一天散步，初始概率，晴天】*【转移概率，晴天】*【发射概率，购物】=0.24*0.6*0.3=0.0432

　　第一天散步+第二天购物的情况下，第一天可能是晴天，第二天也可能是晴天

第三天：

【第三天】【清理】=【初始概率，晴天，下雨】*【转移概率，下雨】*【发射概率，清理】=0.0384*0.7*0.5=0.01344

【第三天】【清理】=【初始概率，晴天，下雨】*【转移概率，晴天】*【发射概率，清理】=0.0384*0.3*0.1=0.00114

【第三天】【清理】=【初始概率，晴天，晴天】*【转移概率，下雨】*【发射概率，清理】=0.0432*0.4*0.5=0.00864

【第三天】【清理】=【初始概率，晴天，晴天】*【转移概率，晴天】*【发射概率，清理】=0.0432*0.6*0.1=0.00259

【第三天】【清理】=【初始概率，下雨，下雨】*【转移概率，下雨】*【发射概率，清理】=0.0168*0.7*0.5=0.00588

【第三天】【清理】=【初始概率，下雨，下雨】*【转移概率，晴天】*【发射概率，清理】=0.0168*0.3*0.1=0.00050

【第三天】【清理】=【初始概率，下雨，晴天】*【转移概率，下雨】*【发射概率，清理】=0.0054*0.4*0.5=0.00108

【第三天】【清理】=【初始概率，下雨，晴天】*【转移概率，晴天】*【发射概率，清理】=0.0054*0.6*0.1=0.00032

　　第一天散步+第二天购物+第三天打扫的情况下，第一天晴天，第二天下雨，第三天下雨概率最大

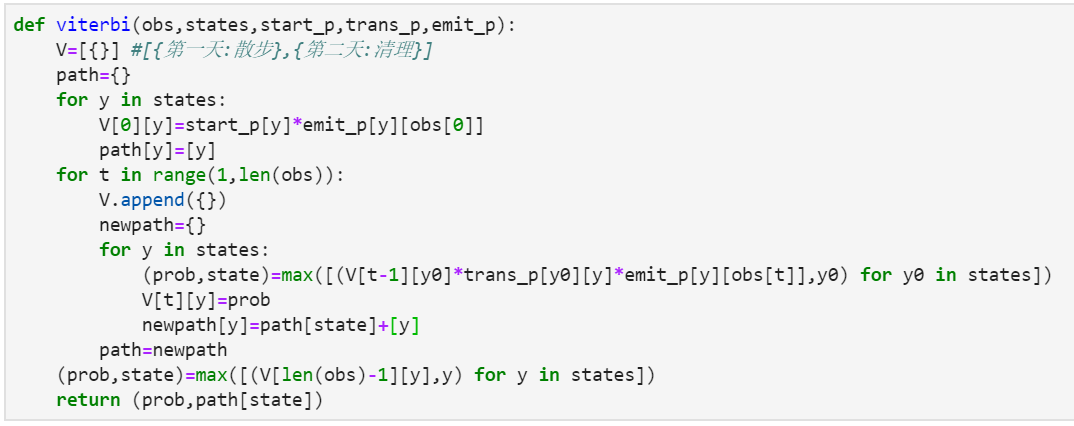
用Python实现：

# Python -version 3.5以上版本

# 打印路径概率表
def print_dptable(V):
    print ("    ",)
    for i in range(len(V)):
        print ("%7d" % i,)
    print ()
    for y in V[0].keys():
        print ("%.5s: " % y,)
        for t in range(len(V)):
            print ("%.7s" % ("%f" % V[t][y]),)
        print ()

def viterbi(obs, states, start_p, trans_p, emit_p):
    # 路径概率表 V[时间][隐含层] = 概率
    V = [{}]
    # 中间变量
    path = {}
    # 状态初始化 (t == 0)
    for y in states:
        V[0][y] = start_p[y] * emit_p[y][obs[0]]
        path[y] = [y]
    # 对 t > 0 跑一遍维特比算法
    for t in range(1, len(obs)):
        V.append({})
        newpath = {}
        for y in states:
            # 概率 隐含层 =  前状态是y0的初始概率 * y0转移到y的转移概率 * y表现为当前状态的发射概率
            (prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
            # 记录最大概率
            V[t][y] = prob
            # 记录路径
            newpath[y] = path[state] + [y]
        path = newpath
    print_dptable(V)
    (prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
    return (prob, path[state])

# HMM 实例导入
states = ('Rainy', 'Sunny')
observations = ('walk', 'shop', 'clean')
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
transition_probability = {
    'Rainy': {'Rainy': 0.7, 'Sunny': 0.3},
    'Sunny': {'Rainy': 0.4, 'Sunny': 0.6},
}
emission_probability = {
    'Rainy': {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
    'Sunny': {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}

def example():
    #将实例值传输到viterbi函数
    return viterbi(observations,
                   states,
                   start_probability,
                   transition_probability,
                   emission_probability
                   )
print (example())