POJ 2697 A Board Game（Trie判重+BFS）

A Board Game

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 551		Accepted: 373

Description

Dao was a simple two-player board game designed by Jeff Pickering and Ben van Buskirk at 1999. A variation of it, called S-Dao, is a one-player game. In S-Dao, the game board is a 4 * 4 square with 16 cells. There are 4 black stones and 4 white stones placed on the game board randomly in the beginning. The player is given a final position and asked to play the game using the following rules such that the final position is reached using the minimum number of moves:

1. You first move a white stone, and then a black stone. You then alternatively move a white stone and a black stone.

2. A stone can be moved horizontally, vertically or diagonally. A stone must be moved in a direction until the boarder or another stone is encountered. There is no capture or jump.

3. During each move, you need to move a stone of the right color. You cannot pass.

An example of a sequence of legal moves is shown in the following figure. This move sequence takes 4 moves. This is not a sequence of legal moves 
 
using the least number of moves assume the leftmost board is the initial position and the rightmost board is the final position. A sequence of moves using only 3 moves is shown below. 
 
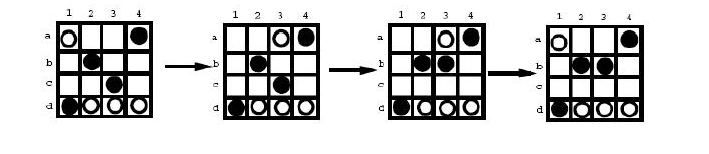
Given an initial position and a final position, your task is to report the minimum number of moves from the initial position to the final position.

Input

The first line contains the number of test cases w, w <= 6. Then the w test cases are listed one by one. Each test case consists of 8 lines, 4 characters per line. The first 4 lines are the initial board position. The remaining 4 lines are the final board position. The i-th line of a board is the board at the i-th row. A character 'b' means a black stone, a character 'w' means a white stone, and a '*' means an empty cell.

Output

For each test case, output the minimum number of moves in one line. If it is impossible to move from the initial position to the final position, then output -1.

Sample Input

2
w**b
*wb*
*bw*
b**w
w**b
*wb*
*bw*
bw**
w**b
*b**
**b*
bwww
w**b
*bb*
****
bwww

Sample Output

1
3

题目链接：POJ 2697

题如其名，很无聊，难怪题目里的S-Dao是一个人玩的游戏，给你一个4*4的棋盘和4颗黑棋、4颗白旗，每一次可以向八个方向移动，但是只能撞到边界或者撞到棋子才能停止移动，求初始态到目标态最少的移动次数，这题由于每个格子的颜色不是唯一的，康托不好用，只能用STL或者字典树，然后看一共有多少种状态，显然是$\binom{16}{4} * \binom{12}{4} = 900900$，然而想想STL这么慢还是字典树吧，顺便再熟练一下数组版字典树的写法，虽然代码量有点大，但是细心点还是不会错的，写斜方向移动函数的时候突然感觉有点想起以前玩魔方的公式了，怀念1s。

代码：

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <sstream>
#include <cstring>
#include <bitset>
#include <string>
#include <deque>
#include <stack>
#include <cmath>
#include <queue>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
typedef pair<int,int> pii;
typedef long long LL;
const double PI=acos(-1.0);
const int N=900900+7;
struct info
{
    char st[4][4];
    bool bw;
    int step;
    inline bool operator==(const info &t)const
    {
        for (int i=0; i<4; ++i)
            for (int j=0; j<4; ++j)
                if(st[i][j]!=t.st[i][j])
                    return false;
        return true;
    }
    inline void Lmove(const int &x,const int &y)
    {
        int yy=y;
        while (yy-1>=0&&st[x][yy-1]=='0')
            --yy;
        swap(st[x][y],st[x][yy]);
        ++step;
        bw^=1;
    }
    inline void Rmove(const int &x,const int &y)
    {
        int yy=y;
        while (yy+1<4&&st[x][yy+1]=='0')
            ++yy;
        swap(st[x][y],st[x][yy]);
        ++step;
        bw^=1;
    }
    inline void Umove(const int &x,const int &y)
    {
        int xx=x;
        while (xx-1>=0&&st[xx-1][y]=='0')
            --xx;
        swap(st[x][y],st[xx][y]);
        ++step;
        bw^=1;
    }
    inline void Dmove(const int &x,const int &y)
    {
        int xx=x;
        while (xx+1<4&&st[xx+1][y]=='0')
            ++xx;
        swap(st[x][y],st[xx][y]);
        ++step;
        bw^=1;
    }
    inline void RU(const int &x,const int &y)
    {
        int xx=x;
        int yy=y;
        while (xx-1>=0&&yy+1<4&&st[xx-1][yy+1]=='0')
            --xx,++yy;
        swap(st[x][y],st[xx][yy]);
        ++step;
        bw^=1;
    }
    inline void RD(const int &x,const int &y)
    {
        int xx=x;
        int yy=y;
        while (xx+1<4&&yy+1<4&&st[xx+1][yy+1])
            ++xx,++yy;
        swap(st[x][y],st[xx][yy]);
        ++step;
        bw^=1;
    }
    inline void LU(const int &x,const int &y)
    {
        int xx=x;
        int yy=y;
        while (xx-1>=0&&yy-1>=0&&st[xx-1][yy-1]=='0')
            --xx,--yy;
        swap(st[x][y],st[xx][yy]);
        ++step;
        bw^=1;
    }
    inline void LD(const int &x,const int &y)
    {
        int xx=x;
        int yy=y;
        while (xx+1<4&&yy-1>=0&&st[xx+1][yy-1]=='0')
            ++xx,--yy;
        swap(st[x][y],st[xx][yy]);
        ++step;
        bw^=1;
    }
};
struct Trie
{
    int nxt[3];
    inline void init()
    {
        nxt[0]=nxt[1]=nxt[2]=0;
    }
};
Trie L[N*3];
int tot;
info S,T;
enum {B=true,W=false};

void init()
{
    L[0].init();
    tot=1;
}
bool update(const info &t)
{
    int now=0;
    bool any=false;
    for (int i=0; i<16; ++i)
    {
        int v=t.st[i>>2][i%4]-'0';
        if(!L[now].nxt[v])
        {
            L[tot].init();
            L[now].nxt[v]=tot++;
            any=true;
        }
        now=L[now].nxt[v];
    }
    return any;
}
int bfs(const info &s)
{
    queue<info>Q;
    Q.push(s);
    update(s);
    info now,v;
    while (!Q.empty())
    {
        now=Q.front();
        if(now==T)
            return now.step;
        Q.pop();
        if(!now.bw)///白色
        {
            for (int i=0; i<16; ++i)
            {
                if(now.st[i>>2][i%4]=='1')
                {
                    v=now;
                    v.Dmove(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.Umove(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.Lmove(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.Rmove(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.LU(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.RU(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.LD(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                }
            }
        }
        else///黑色
        {
            for (int i=0; i<16; ++i)
            {
                if(now.st[i>>2][i%4]=='2')
                {
                    v=now;
                    v.Dmove(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.Umove(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.Lmove(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.Rmove(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.LU(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.RU(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                    v=now;
                    v.LD(i>>2,i%4);
                    if(update(v))
                        Q.push(v);
                }
            }
        }
    }
    return -1;
}
int main(void)
{
    int tcase,i,j;
    scanf("%d",&tcase);
    getchar();
    while (tcase--)
    {
        init();
        for (i=0; i<4; ++i)
        {
            for (j=0; j<4; ++j)
            {
                scanf("%c",&S.st[i][j]);
                if(S.st[i][j]=='*')
                    S.st[i][j]='0';
                else if(S.st[i][j]=='w')
                    S.st[i][j]='1';
                else
                    S.st[i][j]='2';
            }
            getchar();
        }
        S.step=0;
        S.bw=W;
        for (i=0; i<4; ++i)
        {
            for (j=0; j<4; ++j)
            {
                scanf("%c",&T.st[i][j]);
                if(T.st[i][j]=='*')
                    T.st[i][j]='0';
                else if(T.st[i][j]=='w')
                    T.st[i][j]='1';
                else
                    T.st[i][j]='2';
            }
            getchar();
        }
        printf("%d\n",bfs(S));
    }
    return 0;
}