Candies---hdu3159（spfa+差分约束）

题目链接：http://poj.org/problem?id=3159

题意:有n个小孩，m个关系格式是A B C 表示小孩 B 的糖果数最多比小孩A多C个，相当于B-A<=C;

有m个这样的关系最后求小孩n比小孩1最多多几个糖果；

差分约束：

比如给出三个不等式,b-a<=k1,c-b<=k2,c-a<=k3,求出c-a的最大值, 我们可以把a,b,c转换成三个点，k1，k2，k3是边上的权，如图

 

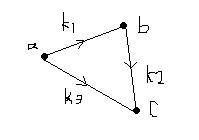
由题我们可以得知，这个有向图中，由题b-a<=k1,c-b<=k2,得出c-a<=k1+k2,因此比较k1+k2和k3的大小，求出最小的就是c-a的最大值了

根据以上的解法，我们可能会猜到求解过程实际就是求从a到c的最短路径，没错的....简单的说就是从a到c沿着某条路径后把所有权值和k求出就是c -a<=k的一个

推广的不等式约束，既然这样，满足题目的肯定是最小的k，也就是从a到c最短距离...

然而本题就是直接求1到n的最短距离即可；

直接用队列会TLE，所以要用优先队列，或者用栈也能过；

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <queue>
#include <stack>
#include <algorithm>
#include <map>
#include <string>
typedef long long LL;
#define INF 0x3f3f3f3f
#define met(a, b) memset(a, b, sizeof(a))
#define N 150100

using namespace std;

struct node
{
    int v, w, Next;
    friend bool operator < (node p, node q)
    {
        return p.w > q.w;
    }
}e[N];

int Head[N], cnt, n, dist[N], vis[N];

void Add(int u, int v, int w)
{
    e[cnt].v = v;
    e[cnt].w = w;
    e[cnt].Next = Head[u];
    Head[u] = cnt++;
}

int spfa(int s)
{
    for(int i=; i<=n; i++)
    {
        dist[i] = INF;
        vis[i] = ;
    }

    priority_queue<node> Q;
    vis[s] = ;
    dist[s] = ;

    node p, q;
    p.v = s;p.w = ;

    Q.push(p);
    while(!Q.empty())
    {
        p = Q.top(); Q.pop();
        vis[p.v] = ;
        for(int i=Head[p.v]; i!=-; i=e[i].Next)
        {
            q.v = e[i].v;
            if(dist[q.v] > dist[p.v]+e[i].w)
            {
                dist[q.v] = dist[p.v]+e[i].w;
                if(!vis[q.v])
                {
                    vis[q.v] = ;
                    q.w  = dist[q.v];
                    Q.push(q);
                }
            }
        }
    }
    return dist[n];
}

int main()
{
    int m, u, v, w;
    while(scanf("%d %d", &n, &m) != EOF)
    {
        met(e, );
        met(Head, -);
        cnt = ;
        for(int i=; i<=m; i++)
        {
            scanf("%d %d %d", &u, &v, &w);
            Add(u, v, w);
        }
        int ans = spfa();
        printf("%d\n", ans);
    }
    return ;
}