P1273 有线电视网（树形动规，分组背包）

题目链接：

https://www.luogu.org/problemnew/show/P1273

题目描述

某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构，这棵树的根结点位于足球比赛的现场，树叶为各个用户终端，其他中转站为该树的内部节点。

从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的，一场转播的总费用等于传输信号的费用总和。

现在每个用户都准备了一笔费用想观看这场精彩的足球比赛，有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。

写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。

输入输出格式

输入格式：

输入文件的第一行包含两个用空格隔开的整数N和M，其中2≤N≤3000，1≤M≤N-1，N为整个有线电视网的结点总数，M为用户终端的数量。

第一个转播站即树的根结点编号为1，其他的转播站编号为2到N-M，用户终端编号为N-M+1到N。

接下来的N-M行每行表示—个转播站的数据，第i+1行表示第i个转播站的数据，其格式如下：

K A1 C1 A2 C2 … Ak Ck

K表示该转播站下接K个结点(转播站或用户)，每个结点对应一对整数A与C，A表示结点编号，C表示从当前转播站传输信号到结点A的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。

输出格式：

输出文件仅一行，包含一个整数，表示上述问题所要求的最大用户数。

输入输出样例

输入样例#1： 复制
5 3
2 2 2 5 3
2 3 2 4 3
3 4 2
输出样例#1： 复制
2

思路：

节点与节点之间具有先后的依赖关系，在本题中表现为只有先选择中转接点才能访问到叶子节点。

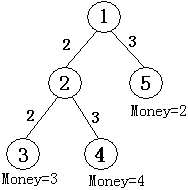
以题目给定的样例为例，如果要访问3,4节点必须先经过2，在这里假设f[u][j]为节点为u时选择前j个节点获得的最大利润，以f[1][j]来说，他最多可以选择的节点分别是3,4,5三个节点，但是3,4这两个节点必须先经过2。那么f[1][j]可以表示成：$f[1][j]=max(f[1][j],f[1][j-k]+f[son][k]-edge[1][son])$，其中k表示1的前k个节点，edge[1][son]表示节点1和他的孩子之间的边。这里可以看成是节点1选择k个孩子，但这k个孩子是由下一层节点回溯上来的。

每一个中转节点相当于一个大的背包，中转节点的孩子相当于背包里面的商品，如果背包容量为k，那么可以在这里背包里面选择1~k个商品。然后中转节点在向上层节点回溯，最后汇聚到根节点。

初始化每个节点为负无穷大，最后根据根节点f[1][j]来判断可以有多少孩子满足条件。

#include<bits/stdc++.h>
using namespace std;
#define mp make_pair
#define pb push_back
vector<pair<int,int> > ed[3005];
int n,m;
int v[3005];
int f[3005][3005];
int dfs(int u){
//    printf("%d\n",u);
    if(u>n-m){
        f[u][1]=v[u];
        return 1;
    }

    int sum=0;
    for(auto to:ed[u]){
        int nxt=to.first,d=to.second;
        int t=dfs(nxt);
        sum+=t;

        for(int j=sum;j>0;j--){
            for(int i=1;i<=t;i++){
                if(j-i>=0)
                    f[u][j]=max(f[u][j],f[u][j-i]+f[nxt][i]-d);
            }
        }
    }

    return sum;
}
int main(){

    scanf("%d %d",&n,&m);
    for(int i=1;i<=n-m;i++){
        int k;
        scanf("%d",&k);
        while(k--){
            int nd,w;
            scanf("%d %d",&nd,&w);
            ed[i].pb(mp(nd,w));
        }
    }
    for(int i=n-m+1;i<=n;i++) scanf("%d",&v[i]);//    memset(f,-0x3f3f3f3f,sizeof(f));
    fill(f[0],f[0]+3005*3005,-0x3f3f3f3f);
    for(int i=1;i<=n;i++) f[i][0]=0;

    dfs(1);
    for(int j=m;j>0;j--){
        if(f[1][j]>=0){
            printf("%d\n",j);
            break;
        }
    }
    return 0;
}