趁着503的清早 我还算清醒把昨天老师讲的内容总结一下，昨天有点迷了 至使我A的几道题都迷迷糊糊的。（可能是我太菜了）

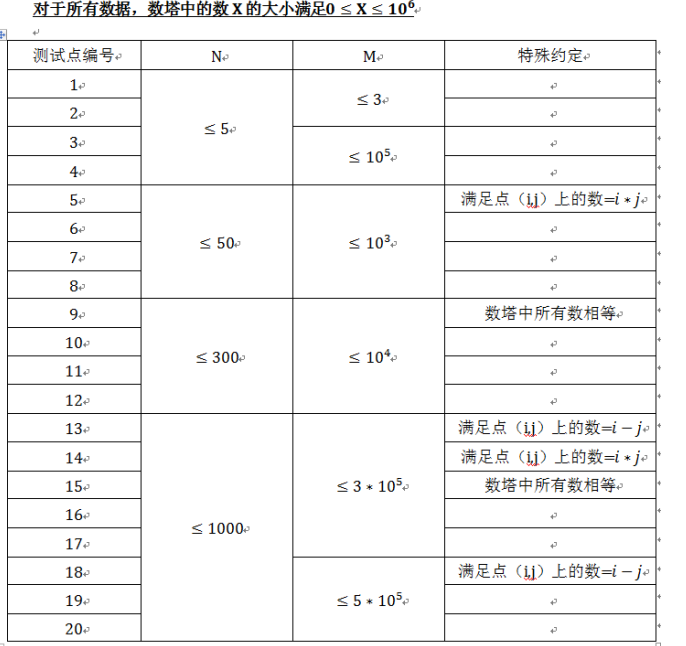
这道题显然是 数字三角形的变形 好没有经过认真思考然后直接暴力了 这是很不应该的 但正解 是需要你能深刻理解数字三角形的模板式究竟是什么含义这显然是我这种 感觉很简单的东西没有认真思考每一个f值所以造成这道题没有写出正解。

bf: 求出一条答案路径，如果询问在这条路径上那就直接暴力跑一遍不在的话直接输出最大值 复杂度n^3 实际低分很低貌似写挂了。

当然 100分的做法也很简单 我们只需考虑原本的f数组的含义表示右上到下到此点的最大的和。

对于一个答案显然是某一行中的一个点的由上到下和由下到上的和。 于是可以加一个数组g[i][j]表示右下到上的到达这个点的最大和。

显然 对于ban掉的一个点，不在1,1 那就不是-1 然后次大值是由 当前这行旁边的点构成的 那么我们再在当前这行再求一个次大值直接用f 和g数组求即可。解法就是这样了 对于每一行求出最大值 求出最大值 路径 求出次大值，询问输出即可。n^2

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cmath>

#include<cstdio>

#include<ctime>

#include<queue>

#include<stack>

#include<vector>

#include<cctype>

#include<utility>

#include<algorithm>

#include<cstring>

#include<string>

#include<map>

#include<set>

#include<bitset>

#include<deque>

#include<cstdlib>

#define INF 2147483646

#define ll long long

#define db double

#define min(x,y) (x>y?y:x)

#define max(x,y) (x>y?x:y)

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=;

int n,m,s1,s2,t;

int ans,maxx;

int a[MAXN][MAXN];

int b[MAXN],vis[MAXN][MAXN];

int f[MAXN][MAXN];

int g[MAXN][MAXN],w[MAXN][MAXN];//f[i][j]表示到了第i j个点所得到的价值最大

int main()

{

    //freopen("1.in","r",stdin);

    freopen("tower.in","r",stdin);

    freopen("tower.out","w",stdout);

    memset(a,,sizeof(a));

    n=read();m=read();

    for(int i=;i<=n;++i)

        for(int j=;j<=i;++j)

            a[i][j]=read();

    for(int i=;i<=n;++i)

        for(int j=;j<=i;++j)

        {

            f[i][j]=max(f[i][j],f[i-][j]+a[i][j]);

            f[i][j]=max(f[i][j],f[i-][j-]+a[i][j]);

        }

    for(int i=n;i>=;--i)for(int j=;j<=i;++j)

    {

        g[i][j]=max(g[i][j],g[i+][j]+a[i][j]);

        g[i][j]=max(g[i][j],g[i+][j+]+a[i][j]);

    }

    //for(int i=1;i<=n;++i)maxx=max(maxx,f[n][i]);

    maxx=g[][];

    for(int i=;i<=n;++i)

    {

        for(int j=;j<=i;++j)if(g[i][j]+f[i][j]-a[i][j]==maxx){vis[i][j]=;break;}

        for(int j=;j<=i;++j)

        {

            if(vis[i][j])continue;

            b[i]=max(g[i][j]+f[i][j]-a[i][j],b[i]);

            //cout<<b[i]<<endl;

        }

    }

    //puts("");

    for(int i=;i<=m;++i)

    {

        int x,y;

        x=read();y=read();

        //cout<<vis[x][y]<<endl;

        if(x==&&y==){puts("-1");continue;}

        if(vis[x][y])put(b[x]);

        else put(maxx);

    }

    return ;

}

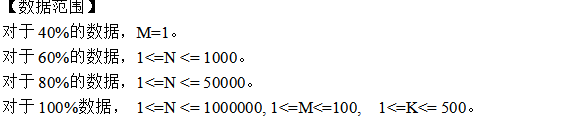
这道题 就很有意思了，是这几道题我暴力都写的比较难受的一道想出设多维来想办法进行状态转移 我觉得不管怎样转移都是具有极强的后效性的，2h后放弃了对于m==1的情况 我写了一个n^2k的暴力dp 写完了还觉得没什么问题 事实上我这种做法是不必要的。

考虑 m==1怎么写其实无非就是对于一个长度为n的序列 分成m+1段然后使每一段的价值等差数列的和的和最小。其实直接分就好了不需要dp

可能很显然的想出这是正确的，然后 无非是余数的问题 考虑每一段后都跟一个余数直至把余数数完。

那对于每一个窝的 我们使用k次以后这个窝所带来的价值 其实现在问题再次转换 转换成了 m个窝 k次清空操作 然后询问最小价值。

显然了 这是一个资源分配类型的dp 直接dp 转移一下就好了。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cmath>

#include<cstdio>

#include<ctime>

#include<queue>

#include<stack>

#include<vector>

#include<cctype>

#include<utility>

#include<algorithm>

#include<cstring>

#include<string>

#include<map>

#include<set>

#include<bitset>

#include<deque>

#include<cstdlib>

#define ll long long

#define db double

#define min(x,y) (x>y?y:x)

#define INF 21474836460000000ll

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(ll x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=,maxn=,Maxn=;

ll n,m,p,T;

ll ans;

ll a[MAXN],c[maxn];

//对于 m==1 显然采用贪心可以 将一段序列分成p+1段的最小值 取平均即可

ll w[maxn][Maxn];//w[i][j]表示 对于第i种物品分成j段的代价

ll f[maxn][Maxn];//表示前i种牛分配到j个清理 得到了多少价值

ll cost(ll x,ll y)

{

    ++y;

    ll cnt=x/y;

    ll mod=x%y;

    return ((cnt+)*cnt/)*y+mod*(cnt+);

}

int main()

{

    //freopen("1.in","r",stdin);

    freopen("noise.in","r",stdin);

    freopen("noise.out","w",stdout);

    n=read();m=read();p=read();

    for(int i=;i<=n;++i)a[i]=read(),++c[a[i]];

    for(int i=;i<=m;++i)

        for(int j=;j<=p;++j)w[i][j]=cost(c[i],j);

    for(int i=;i<=m;++i)

        for(int j=;j<=p;++j)

        {

            f[i][j]=INF;

            for(int k=;k<=j;++k)

                f[i][j]=min(f[i][j],f[i-][k]+w[i][j-k]);

        }

    put(f[m][p]);

    return ;

}

其实很简单 但是针对m==1的情况我没有好好的思考所以 造成了整道题的崩溃。或者说我对模板只是感觉简单并没有利用它。

值得一提的是上述式子还可以进行单调性优化时间复杂度为mk 发现n>mk时间复杂度为O(n)(哇如此优秀。

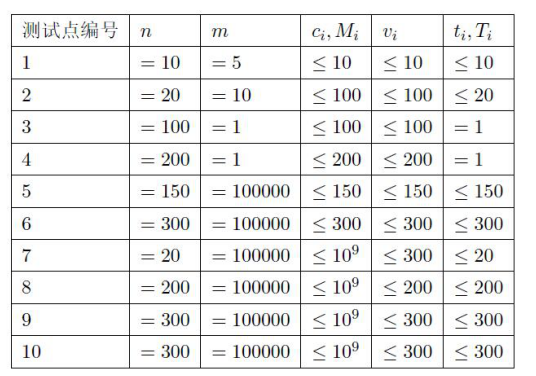
这道题的暴力超级好 直接01背包都有40分 加两个排序可以做到Mn的复杂度了。期望得分60 实际得分：60；

考虑后40分怎么办。看出M非常的大v非常的小 这又是01背包的变换形式了 仔细思考我们背包是根据容量来确定价值的，容量一定价值一定、

那如果是根据价值来确定容量呢 这样的01背包也是可以的吧 这样就价值为多少的时候 需要的金钱数。

显然 这个01背包的变形 是没有那么简单的，需要考虑 时间 这个我们按照时间排序物品即可。然后在f数组里进行二分查找即可。

细节需要处理 f数组可能不具单调性 O(n)扫一遍使其具有单调性即可。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cmath>

#include<cstdio>

#include<ctime>

#include<queue>

#include<stack>

#include<vector>

#include<cctype>

#include<utility>

#include<algorithm>

#include<cstring>

#include<string>

#include<map>

#include<set>

#include<bitset>

#include<deque>

#include<cstdlib>

#define ll long long

#define db double

#define min(x,y) (x>y?y:x)

#define INF 21474836460000ll

#define v(x) t[x].v

#define w(x) t[x].w

#define ti(x) t[x].ti

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=,maxn=;

int n,m,maxx,flag=;

struct wy

{

    int w,v,ti;

    int friend operator <(wy x,wy y){return x.ti<y.ti;}

}t[maxn];

struct wy1

{

    int x,y;//x为时间y为金钱

}s[MAXN];

ll f[maxn][maxn*maxn];//f[i][j]表示前i个物品 价值为j的最小花费

inline int find(int xx)

{

    int l=,r=n;

    while(l+<r)

    {

        int mid=(l+r)>>;

        if(ti(mid)<=xx)l=mid;

        else r=mid;

    }

    if(ti(r)<=xx)return r;

    return l;

}

inline int carculate(int i,int x)

{

    int l=,r=maxx;

    while(l+<r)

    {

        int mid=(l+r)>>;

        if(f[i][mid]<=x)l=mid;

        else r=mid;

    }

    if(f[i][r]<=x)return r;

    return l;

}

int main()

{

    //freopen("1.in","r",stdin);

    freopen("market.in","r",stdin);

    freopen("market.out","w",stdout);

    n=read();m=read();

    for(int i=;i<=n;++i)

    {

        w(i)=read();

        v(i)=read();

        ti(i)=read();

        maxx+=v(i);

    }

    //put(maxx);

    sort(t+,t++n);

    for(int i=;i<=m;++i)s[i].x=read(),s[i].y=read();

    for(int i=;i<=maxx;++i)f[][i]=INF;

    f[][]=;

    for(int i=;i<=n;i++)

        for(int j=maxx;j>=;j--)

        {

            f[i][j]=f[i-][j];

            if(j>=v(i))f[i][j]=min(f[i-][j-v(i)]+w(i),f[i][j]);

        }

    for(int i=;i<=n;++i)

        for(int j=maxx-;j>=;--j)f[i][j]=min(f[i][j+],f[i][j]);

    for(int i=;i<=m;++i)

    {

        int xx=find(s[i].x);

        //put(xx);

        put(carculate(xx,s[i].y));

    }

    return ;

}

值得一提的是01二维01背包 注意不要少一句话承接上一层的值 我wa了半天因为这个。时间复杂度为 n*价值和+mlogn+mlog价值和+nlogn

一维的01背包 时间复杂度 n*价值和+nlogn+mlogm+mlogm+mlogm上下比较上面更为优秀 少了两次排序对了一次二分查找。

代码中的细节还算是比较ex的 调了一会才发现又犯sb错误。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cmath>

#include<cstdio>

#include<ctime>

#include<queue>

#include<stack>

#include<vector>

#include<cctype>

#include<utility>

#include<algorithm>

#include<cstring>

#include<string>

#include<map>

#include<set>

#include<bitset>

#include<deque>

#include<cstdlib>

#define ll long long

#define db double

#define min(x,y) (x>y?y:x)

#define INF 21474836460000ll

#define v(x) t[x].v

#define w(x) t[x].w

#define ti(x) t[x].ti

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=,maxn=;

int n,m,maxx,flag=;

struct wy

{

    int w,v,ti;

    int friend operator <(wy x,wy y){return x.ti<y.ti;}

}t[maxn];

struct wy1

{

    int x,y;//x为时间y为金钱

    int id;

    int ans;

}s[MAXN];

int cmp(wy1 a,wy1 b){return a.x<b.x;}

int cmp1(wy1 a,wy1 b){return a.id<b.id;}

ll f[maxn*maxn];//f[i][j]表示前i个物品 价值为j的最小花费

inline int carculate(int x)

{

    int l=,r=maxx;

    while(l+<r)

    {

        int mid=(l+r)>>;

        if(f[mid]<=x)l=mid;

        else r=mid;

    }

    if(f[r]<=x)return r;

    return l;

}

int main()

{

    //freopen("1.in","r",stdin);

    freopen("market.in","r",stdin);

    freopen("market.out","w",stdout);

    n=read();m=read();

    for(int i=;i<=n;++i)

    {

        w(i)=read();

        v(i)=read();

        ti(i)=read();

        maxx+=v(i);

    }

    //put(maxx);

    sort(t+,t++n);

    for(int i=;i<=m;++i)s[i].x=read(),s[i].y=read(),s[i].id=i;

    sort(s+,s++m,cmp);

    for(int i=;i<=maxx;++i)f[i]=INF;

    for(int i=;i<=n;++i)

    {

        if(s[flag].x<ti(i)&&flag<=m)

            for(int j=maxx-;j>=;--j)f[j]=min(f[j],f[j+]);

        while(s[flag].x<ti(i)&&flag<=m)s[flag].ans=carculate(s[flag].y),++flag;

        for(int j=maxx;j>=v(i);--j)f[j]=min(f[j],f[j-v(i)]+w(i));

    }

    if(flag<=m)for(int j=maxx-;j>=;--j)f[j]=min(f[j],f[j+]);

    for(int i=flag;i<=m;++i)s[i].ans=carculate(s[i].y);

    sort(s+,s++m,cmp1);

    for(int i=;i<=m;++i)put(s[i].ans);

    return ;

}

这道题 我感觉是上面的题目中最难的题目原因是 感觉无论怎么选后效性极强。于是对着40分写了一个爆搜。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cmath>

#include<cstdio>

#include<ctime>

#include<queue>

#include<stack>

#include<vector>

#include<cctype>

#include<utility>

#include<algorithm>

#include<cstring>

#include<string>

#include<map>

#include<set>

#include<bitset>

#include<deque>

#include<cstdlib>

#define ll long long

#define db double

#define min(x,y) (x>y?y:x)

#define INF 2147483646

#define v(x) t[x].v

#define w(x) t[x].w

#define ti(x) t[x].ti

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=;

int n,ans;

int vis[MAXN],v[MAXN],w[MAXN];

int q[MAXN],t;

void dfs(int depth)

{

    if(depth<=n&&depth)

    {

        int cnt=,sum=;

        for(int i=;i<=depth;++i)

        {

            sum+=v[q[i]]-cnt;

            cnt+=w[q[i]];

        }

        ans=max(ans,sum);

        if(depth==n)return;

    }

    for(int i=;i<=n;++i)

    {

        if(vis[i]==)

        {

            q[depth+]=i;

            vis[i]=;

            dfs(depth+);

            vis[i]=;

        }

    }

}

int main()

{

    //freopen("1.in","r",stdin);

    freopen("value.in","r",stdin);

    freopen("value.out","w",stdout);

    n=read();

    if(n<=)

    {

        for(int i=;i<=n;++i)v[i]=read(),w[i]=read();

        dfs();

    }

    put(ans);

    return ;

}

显然爆搜不是搜全排列连子排列都要搜出来。然后计算答案即可。复杂度 8！其实子排列可以创造出全排列所以 复杂度认为8！

那好我要开车了，针对这道题老师也是点了一下思路接下来是我今天的分析这道题怎么写。

1 首先我们要选的话一定选wi较小的，因为我们如果还想选下一个的话 首先对于这两个物品 其最小的wi必然是被先选的 然后剩下的那个价值量会减小很少的 如果选wi较大的那么价值就会减小很大。反而不优了。需要按wi排一下序。

2 首先我们f[i][j]表示前i件物品选择j件物品的最大价值那么此时价值会灰常不好算因为我们不知道后面还要选多少个物品。

3 那么显然 f[i][j]表示前i件物品中选择后j个物品的最大价值。这样来进行就可以了。

注意排序是必然的因为 wi较小的选择是必然的 而且观察我们这个状态 选择了后j个物品 显然这个选择了后j个物品我们进行状态转移时如果不倒序就无法进行有效的状态转移，因为你的状态为空。当然记忆化搜索也行 反正都是拓扑序。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cmath>

#include<cstdio>

#include<ctime>

#include<queue>

#include<stack>

#include<vector>

#include<cctype>

#include<utility>

#include<algorithm>

#include<cstring>

#include<string>

#include<map>

#include<set>

#include<bitset>

#include<deque>

#include<cstdlib>

#define ll long long

#define db double

#define min(x,y) (x>y?y:x)

#define INF 2147483646

#define v(x) t[x].v

#define w(x) t[x].w

#define ti(x) t[x].ti

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=;

int n,maxx;

int f[MAXN][MAXN];//f[i][j] 表示 对于前i个物品 后面选择j个物品的最大价值

struct wy

{

    int v,w;

    int friend operator <(wy x,wy y)

    {

        return x.w>y.w;

    }

}t[MAXN];

int main()

{

    freopen("1.in","r",stdin);

    //freopen("value.in","r",stdin);

    //freopen("value.out","w",stdout);

    n=read();

    for(int i=;i<=n;++i)v(i)=read(),w(i)=read();

    sort(t+,t++n);

    //for(int i=1;i<=n;++i)cout<<w(i)<<endl;

    for(int i=;i<=n;++i)

    {

        for(int j=;j<=i;++j)

        {

            f[i][j]=max(f[i-][j],f[i-][j-]+v(i)-w(i)*(j-));

            maxx=max(maxx,f[i][j]);

        }

    }

    put(maxx);

    return ;

}

对于这道题 其实最暴力也最简单的是最短路问题 由于是树也就最短路只有一条直接dfs即可 然后也变成了一个树形换根dp

所幸这道题比较简单我仔细思考之后是独立的写出来了 这种换根还是比较简单的。

考虑到我们已经求出的东西能给我们带来什么效果。

设出f[i][0]表示以其为根的子树内到此点的距离之和 d[i]表示以i为根的子树的人数 f[i][1]表示以i为中心的最小不方便值。

对于我们第一次dfs 求出 f[i][0] & d[i] 此时我以1为根 那么显然 f[1][0]=f[1][1];

然后通过f[1][1] 进行换根dp 状态转移很好推 f[tn][1]=f[tn][0]+f[x][1]-f[tn][0]-d[tn]*e[i]+(cnt-d[tn])*e[i];

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cmath>

#include<cstdio>

#include<ctime>

#include<queue>

#include<stack>

#include<vector>

#include<cctype>

#include<utility>

#include<algorithm>

#include<cstring>

#include<string>

#include<map>

#include<set>

#include<bitset>

#include<deque>

#include<cstdlib>

#define ll long long

#define db double

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline ll read()

{

    ll x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(ll x)

{

    x<?putchar('-'),x=-x:;

    ll num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const ll MAXN=;

ll n,len;

ll cnt,ans=100000000000000000ll;

ll f[MAXN][];//f[i][0]表示以i为根节点且不为集会地点时的方便程度

ll d[MAXN],a[MAXN];//d[i]表示以1为根节点时的牛数

ll lin[MAXN<<],nex[MAXN<<],ver[MAXN<<];

ll e[MAXN<<];

inline ll min(ll x,ll y){return x>y?y:x;}

inline void add(ll x,ll y,ll z)

{

    ver[++len]=y;

    nex[len]=lin[x];

    lin[x]=len;

    e[len]=z;

}

inline void dp(ll x,ll father)

{

    d[x]=a[x];

    for(ll i=lin[x];i;i=nex[i])

    {

        ll tn=ver[i];

        if(tn==father)continue;

        dp(tn,x);

        f[x][]+=d[tn]*e[i]+f[tn][];

        d[x]+=d[tn];

    }

    return;

}

void dfs(ll x,ll father)

{

    for(ll i=lin[x];i;i=nex[i])

    {

        ll tn=ver[i];

        if(tn==father)continue;

        f[tn][]=f[tn][]+(cnt-d[tn])*e[i]+f[x][]-d[tn]*e[i]-f[tn][];

        dfs(tn,x);

    }

    return;

}

int main()

{

    //freopen("1.in","r",stdin);

    freopen("gather.in","r",stdin);

    freopen("gather.out","w",stdout);

    n=read();

    for(ll i=;i<=n;++i)a[i]=read(),cnt+=a[i];

    for(ll i=;i<n;++i)

    {

        ll x,y,z;

        x=read();y=read();z=read();

        add(x,y,z);add(y,x,z);

    }

    dp(,);

    f[][]=f[][];

    dfs(,);

    for(ll i=;i<=n;++i)ans=min(ans,f[i][]);

    //for(ll i=1;i<=n;++i)put(f[i][1]);

    put(ans);

    return ;

}

这是压轴的dp 了我感觉一般吧 还算是比较基础的决策优化 但是这个优化和平常的不太一样 ，我感觉是比较难受的优化。

对于40分考虑一个 n^2的做法 设 f[MAXN];//f[i]表示前i个原子分成若干段的最小代价

显然状态转移f[i]=min(f[i],f[j]+cost[j+1][i]); 当且仅当 j+1~i 不起任何冲突。这个不起冲突我是一个区间dp 来写的麻烦了O(n)即可。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cmath>

#include<cstdio>

#include<ctime>

#include<queue>

#include<stack>

#include<vector>

#include<cctype>

#include<utility>

#include<algorithm>

#include<cstring>

#include<string>

#include<map>

#include<set>

#include<bitset>

#include<deque>

#include<cstdlib>

#define ll long long

#define db double

#define min(x,y) (x>y?y:x)

#define INF 2147483646

#define v(x) t[x].v

#define w(x) t[x].w

#define ti(x) t[x].ti

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=;

int n;

int a[MAXN],b[MAXN];

int w[MAXN][MAXN],cost[MAXN][MAXN];

int f[MAXN];//f[i]表示前i个原子分成若干段的最小代价

int main()

{

    //freopen("1.in","r",stdin);

    freopen("array.in","r",stdin);

    freopen("array.out","w",stdout);

    n=read();

    memset(f,0x3f3f3f3f,sizeof(f));

    for(int i=;i<=n;++i)

    {

        a[i]=read();b[i]=read();

        w[i][i]=;cost[i][i]=b[i];

    }

    for(int len=;len<=n;++len)

    {

        for(int i=;i<=n-len+;++i)

        {

            int j=i+len-;

            w[i][j]|=w[i][j-];

            w[i][j]|=w[i+][j];

            w[i][j]|=(a[i]==a[j]?:);

            cost[i][j]=max(cost[i][j-],b[j]);

        }

    }

    /*for(int i=1;i<=n;++i)

        for(int j=i;j<=n;++j)

            cout<<i<<' '<<j<<' '<<w[i][j]<<endl;*/

    f[]=;

    for(int i=;i<=n;++i)

        for(int j=;j<i;++j)

        {

            if(!w[j+][i])f[i]=min(f[i],f[j]+cost[j+][i]);

        }

    put(f[n]);

    return ;

}

考虑100分的做法 刚刚那个不起冲突可以O(n) 但是总dp式其实就是一个n^2的 优化其实是 观察决策具有单调性。

真的是有单调性啊 尽管不太明显 但是 我仍是为出题人感动 这都有单调性真是为了防AK的题目没有2个小时拿不下来。。（对我来说是这样的

大雾！ 单调性在 很隐秘的地方 首先 对于 f数组 f[j]<=f[i] j<=i f数组单调不下降 对于cost数组呢貌似状似形似 也是一个单调的 是一个单调不上升的 因为如果有一个更大的cost 那么这整个区间都将被更新成这个cost值。一个单调不下降一个单调不上升很烦。这里我们把f[j]可以抽象成一个点 而cost 抽象成一个区间 显然对于cost形成的每一个区间我们选择那个区间最左边的决策时最优秀的。我这样说就把问题规划的很清楚了 我好棒！

其实对于每一个i 最左边的端点 确定然后就是i-最左边端点之中寻找一个 决策使其最优当然对于cost划分的不同的区域我们尽量选择靠近左边的端点这样有了单调性 考虑用什么来维护这个东西 单调队列？貌似不行因为这样的话不只是队首造成贡献了 这个队伍很可能整个都会造成贡献 线段树？

貌似不太行 因为f[j]不会变 cost 会变随着i的增加 这个区域的本质会改变我们修改cost的区间 经过和同学的一番讨论 我 更加深刻的理解了这道题的优化过程 首先是 单调队列 q 维护cost 单调不下降的的区间的左端点 其实就是在众多的不合法区间之内寻找到一个最优的决策。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cmath>

#include<cstdio>

#include<ctime>

#include<queue>

#include<stack>

#include<vector>

#include<cctype>

#include<utility>

#include<algorithm>

#include<cstring>

#include<string>

#include<map>

#include<set>

#include<bitset>

#include<deque>

#include<cstdlib>

#define ll long long

#define db double

#define min(x,y) (x>y?y:x)

#define INF 2147483646

#define v(x) t[x].v

#define w(x) t[x].w

#define ti(x) t[x].ti

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=;

int n,flag;

int a[MAXN],b[MAXN],last[MAXN];

int q[MAXN],l,r;

int f[MAXN];

int main()

{

    //freopen("1.in","r",stdin);

    freopen("array.in","r",stdin);

    freopen("array.out","w",stdout);

    n=read();

    for(int i=;i<=n;++i)a[i]=read(),b[i]=read(),f[i]=INF;

    q[++r]=;++l;

    for(int i=;i<=n;++i)

    {

        if(last[a[i]])flag=max(flag,last[a[i]]);

        last[a[i]]=i;

        while(l<=r&&q[l]<=flag)++l;

        while(l<=r&&b[q[r]]<=b[i])--r;

        q[++r]=i;

        for(int j=l+;j<=r;++j)f[i]=min(f[i],f[q[j-]]+b[q[j]]);

        f[i]=min(f[i],f[flag]+b[q[l]]);

    }

    put(f[n]);

    return ;

}

这个直接在单调队列中寻找决策了 貌似是可以直接加进set里 logn寻找最优决策。

利用find的话直观性很差 但是 可以照着上面的板子打就不容易出现错误了 这里我采用的是迭代器的做法。

其实就很显然了加上一个set 即可 。线段树的我觉得不太行写不了。

set也比较ex的细节 我调了好久而且没有上面好理解 不推荐。

//#include<bits/stdc++.h>

#include<iostream>

#include<iomanip>

#include<cmath>

#include<cstdio>

#include<ctime>

#include<queue>

#include<stack>

#include<vector>

#include<cctype>

#include<utility>

#include<algorithm>

#include<cstring>

#include<string>

#include<map>

#include<set>

#include<bitset>

#include<deque>

#include<cstdlib>

#define ll long long

#define db double

#define min(x,y) (x>y?y:x)

#define max(x,y) (x>y?x:y)

#define INF 2147483646

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(int x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=;

int n,flag;

int a[MAXN],b[MAXN],last[MAXN];

int q[MAXN],l,r;

int f[MAXN],w[MAXN],sum[MAXN];

multiset<int> s;

//multiset<int> :: iterator id[MAXN];

int main()

{

    //freopen("1.in","r",stdin);

    freopen("array.in","r",stdin);

    freopen("array.out","w",stdout);

    n=read();++l;

    for(int i=;i<=n;++i)a[i]=read(),b[i]=read();

    for(int i=;i<=n;++i)

    {

        if(last[a[i]])flag=max(flag,last[a[i]]);

        last[a[i]]=i;

        int k=i-;

        while(l<r&&w[l+]<=flag)s.erase(s.find(sum[l])),++l;

        while(l<=r&&b[q[r]]<=b[i])s.erase(s.find(sum[r])),k=w[r],--r;

        q[++r]=i;w[r]=k;

        if(l!=r)s.insert(f[w[r]]+b[q[r]]),sum[r]=f[w[r]]+b[q[r]],s.erase(s.find(sum[l]));

        s.insert(f[flag]+b[q[l]]);sum[l]=f[flag]+b[q[l]];

        f[i]=*s.begin();

    }

    put(f[n]);

    return ;

}

值得一提的是set的find如果找不到值得话就会返回end 然后删除end 不会RE但是如果最优值冲突后且删除了最优值此时答案就错了。

所以要开multiset 敲黑板正解了 然后 迭代器一直被卡四组数据不知道为什么可能是因为多删除了 还是find好。

那么这几dp 题目总结到这里 关键是观察决策。

老师说 要对模型有深刻的理解 有的时候往往想不出来的问题都是没有把问题转换好 所以才 不会做。

这几道题都是对模型的升华 也算是比较有意义和价值的。

正在做splay搜到了这道题目，以为是splay 半天想不出来怎么写。毒瘤当我准备看题解之时想了想还是dp吧。

设f[i]表示前i本书放入若干个书架的最小花费。咦 f[i]=min(f[i],f[j]+v(j+1~i)) 这和上面 的近乎一模一样啊。

考虑优化我再也不写set优化了，根本搞不出来这玩意。直接单调队列了 发现被卡一个点。吸氧后过了。

// luogu-judger-enable-o2

#include<iostream>

#include<queue>

#include<iomanip>

#include<cctype>

#include<cstdio>

#include<deque>

#include<utility>

#include<cmath>

#include<ctime>

#include<cstring>

#include<string>

#include<cstdlib>

#include<vector>

#include<algorithm>

#include<stack>

#include<map>

#include<set>

#include<bitset>

#define max(x,y) ((x)>(y)?(x):(y))

#define min(x,y) ((x)>(y)?(y):(x))

#define INF 1000000000

#define ll long long

#define l(x) t[x].l

#define r(x) t[x].r

#define sum(x) t[x].sum

#define v(x) t[x].v

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline ll read()

{

    ll x=,f=;char ch=getchar();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}

    return x*f;

}

inline void put(ll x)

{

    x<?putchar('-'),x=-x:;

    ll num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const ll MAXN=;

ll n,m,maxx,cnt,flag;

ll a[MAXN],b[MAXN];

ll f[MAXN];//f[i]表示前i本书放入若干个书架的最小花费。

ll q[MAXN],l,r;

int main()

{

    //freopen("1.in","r",stdin);

    n=read();m=read();

    for(ll i=;i<=n;++i)b[i]=read(),a[i]=read();

    memset(f,0x3f3f3f3f,sizeof(f));

    f[]=;flag=;q[++r]=;++l;

    for(ll i=;i<=n;++i)

    {

        cnt+=a[i];

        while(cnt>m)++flag,cnt-=a[flag-];

        while(l<=r&&q[l]<flag)++l;

        while(l<=r&&b[q[r]]<=b[i])--r;

        q[++r]=i;

        for(ll j=l;j<r;++j)f[i]=min(f[i],f[q[j]]+b[q[j+]]);

        f[i]=min(f[i],f[flag-]+b[q[l]]);

    }

    put(f[n]);

    return ;

}

看题解发现是可以线段树优化的那么我线段树优化好了。调了2h 才发现这种类型的线段树并不是随便优化的。有讲究。

考虑我们线段树中每个点都记录一个最小f值和g值 每次一个新的i过来以后我们直接区间修改因为这是dp的转移。

然后区间查询最小值即可。注意这里的区间修改是维护两个东西H h 一个取max 一个取min 如果当前H<=x直接懒标记了。h>=x直接跳过。

至于最大值的维护我们考虑取最小g 然后加上 当前区间内的一个h 不能乱加也不能那样加总之我写了一个85分代码 发现这点自己维护错了，瞬间比较难受。我们不能那样搞就是 如下维护 g数组不取min 先维护f数组这样贪心我想是错的。

#include<iostream>

#include<queue>

#include<iomanip>

#include<cctype>

#include<cstdio>

#include<deque>

#include<utility>

#include<cmath>

#include<ctime>

#include<cstring>

#include<string>

#include<cstdlib>

#include<vector>

#include<algorithm>

#include<stack>

#include<map>

#include<set>

#include<bitset>

#define max(x,y) ((x)>(y)?(x):(y))

#define min(x,y) ((x)>(y)?(y):(x))

#define INF 10000000000000ll

#define ll long long

#define l(x) t[x].l

#define r(x) t[x].r

#define sum(x) t[x].sum

#define s(x) t[x].s

#define h(x) t[x].h

#define tag(x) t[x].tag

#define g(x) t[x].g

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getc();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getc();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getc();}

    return x*f;

}

inline void put(ll x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=;

int n,m,flag;

int a[MAXN],b[MAXN];

ll f[MAXN],maxx,cnt;//f[i]表示前i本书放入若干个书架的最小花费。

inline ll min1(ll x,ll y){return x>y?y:x;}

inline ll max1(ll x,ll y){return x>y?x:y;}

struct wy

{

    int l,r;

    ll sum,g;

    ll h,s;

    int tag;

}t[MAXN<<];

inline void build(int p,int l,int r)

{

    l(p)=l;r(p)=r;

    if(l==r)return;

    int mid=(l+r)>>;

    build(p<<,l,mid);

    build(p<<|,mid+,r);

    return;

}

inline void pushdown(int p)

{

    tag(p<<)=tag(p<<|)=tag(p);

    s(p<<)=s(p<<|)=h(p<<)=h(p<<|)=tag(p);

    sum(p<<)=g(p<<)+tag(p);

    sum(p<<|)=g(p<<|)+tag(p);

    tag(p)=;return;

}

inline void change(int p,int l,int r,int x)

{

    if(h(p)>=x)return;

    if(l<=l(p)&&r>=r(p))

        if(s(p)<=x)

        {

            tag(p)=x;s(p)=h(p)=x;

            sum(p)=h(p)+g(p);

            return;

        }

    if(tag(p))pushdown(p);

    int mid=(l(p)+r(p))>>;

    if(l<=mid)change(p<<,l,r,x);

    if(r>mid)change(p<<|,l,r,x);

    s(p)=max(s(p<<),s(p<<|));

    h(p)=min(h(p<<),h(p<<|));

    if(sum(p<<)<=sum(p<<|))sum(p)=sum(p<<),g(p)=g(p<<);

    else sum(p)=sum(p<<|),g(p)=g(p<<|);return;

}

inline ll ask(int p,int l,int r)

{

    if(l<=l(p)&&r>=r(p))return sum(p);

    int mid=(l(p)+r(p))>>;

    ll cnt=INF;

    if(tag(p))pushdown(p);

    if(l<=mid)cnt=min1(cnt,ask(p<<,l,r));

    if(r>mid)cnt=min1(cnt,ask(p<<|,l,r));

    s(p)=max(s(p<<),s(p<<|));

    h(p)=min(h(p<<),h(p<<|));

    if(sum(p<<)<=sum(p<<|))sum(p)=sum(p<<),g(p)=g(p<<);

    else sum(p)=sum(p<<|),g(p)=g(p<<|);

    return cnt;

}

inline void insert(int p,int x)

{

    if(l(p)==r(p)){g(p)=f[x];sum(p)=h(p)+g(p);return;}

    int mid=(l(p)+r(p))>>;

    if(tag(p))pushdown(p);

    if(x<=mid)insert(p<<,x);

    else insert(p<<|,x);

    s(p)=max(s(p<<),s(p<<|));

    h(p)=min(h(p<<),h(p<<|));

    //if(x==1)cout<<sum(p<<1)<<' '<<sum(p<<1|1)<<endl;

    if(sum(p<<)<=sum(p<<|))sum(p)=sum(p<<),g(p)=g(p<<);//注意等号

    else sum(p)=sum(p<<|),g(p)=g(p<<|);return;

}

int main()

{

    //freopen("1.in","r",stdin);

    n=read();m=read();

    for(int i=;i<=n;++i)b[i]=read(),a[i]=read();

    build(,,n);f[]=;flag=;

    for(int i=;i<=n;++i)

    {

        cnt+=a[i];

        while(cnt>m)++flag,cnt-=a[flag-];

        change(,flag-,i-,b[i]);

        f[i]=ask(,flag-,i-);

        //cout<<f[i]<<' ';

        if(i!=n)insert(,i);

    }

    put(f[n]);

    return ;

}

然后应先维护g数组加上一个h来更新f数组即可。

#include<iostream>

#include<queue>

#include<iomanip>

#include<cctype>

#include<cstdio>

#include<deque>

#include<utility>

#include<cmath>

#include<ctime>

#include<cstring>

#include<string>

#include<cstdlib>

#include<vector>

#include<algorithm>

#include<stack>

#include<map>

#include<set>

#include<bitset>

#define max(x,y) ((x)>(y)?(x):(y))

#define min(x,y) ((x)>(y)?(y):(x))

#define INF 10000000000000ll

#define ll long long

#define l(x) t[x].l

#define r(x) t[x].r

#define sum(x) t[x].sum

#define s(x) t[x].s

#define h(x) t[x].h

#define tag(x) t[x].tag

#define g(x) t[x].g

using namespace std;

char buf[<<],*fs,*ft;

inline char getc()

{

    return (fs==ft&&(ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++;

}

inline int read()

{

    int x=,f=;char ch=getc();

    while(ch<''||ch>''){if(ch=='-')f=-;ch=getc();}

    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getc();}

    return x*f;

}

inline void put(ll x)

{

    x<?putchar('-'),x=-x:;

    int num=;char ch[];

    while(x)ch[++num]=x%+'',x/=;

    num==?putchar(''):;

    while(num)putchar(ch[num--]);

    putchar('\n');return;

}

const int MAXN=;

int n,m,flag;

int a[MAXN],b[MAXN];

ll f[MAXN],maxx,cnt;//f[i]表示前i本书放入若干个书架的最小花费。

inline ll min1(ll x,ll y){return x>y?y:x;}

inline ll max1(ll x,ll y){return x>y?x:y;}

struct wy

{

    int l,r;

    ll sum,g;

    ll h,s;

    int tag;

}t[MAXN<<];

inline void build(int p,int l,int r)

{

    l(p)=l;r(p)=r;

    if(l==r)return;

    int mid=(l+r)>>;

    build(p<<,l,mid);

    build(p<<|,mid+,r);

    return;

}

inline void pushdown(int p)

{

    tag(p<<)=tag(p<<|)=tag(p);

    s(p<<)=s(p<<|)=h(p<<)=h(p<<|)=tag(p);

    sum(p<<)=g(p<<)+tag(p);

    sum(p<<|)=g(p<<|)+tag(p);

    tag(p)=;return;

}

inline void change(int p,int l,int r,int x)

{

    if(h(p)>=x)return;

    if(l<=l(p)&&r>=r(p))

        if(s(p)<=x)

        {

            tag(p)=x;s(p)=h(p)=x;

            sum(p)=h(p)+g(p);

            return;

        }

    if(tag(p))pushdown(p);

    int mid=(l(p)+r(p))>>;

    if(l<=mid)change(p<<,l,r,x);

    if(r>mid)change(p<<|,l,r,x);

    s(p)=max(s(p<<),s(p<<|));

    h(p)=min(h(p<<),h(p<<|));

    g(p)=min(g(p<<),g(p<<|));

    sum(p)=min(sum(p<<),sum(p<<|));

}

inline ll ask(int p,int l,int r)

{

    if(l<=l(p)&&r>=r(p))return sum(p);

    int mid=(l(p)+r(p))>>;

    ll cnt=INF;

    if(tag(p))pushdown(p);

    if(l<=mid)cnt=min1(cnt,ask(p<<,l,r));

    if(r>mid)cnt=min1(cnt,ask(p<<|,l,r));

    s(p)=max(s(p<<),s(p<<|));

    h(p)=min(h(p<<),h(p<<|));

    sum(p)=min(sum(p<<),sum(p<<|));

    g(p)=min(g(p<<),g(p<<|));

    return cnt;

}

inline void insert(int p,int x)

{

    if(l(p)==r(p)){g(p)=f[x];return;}

    int mid=(l(p)+r(p))>>;

    if(tag(p))pushdown(p);

    if(x<=mid)insert(p<<,x);

    else insert(p<<|,x);

    g(p)=min(g(p<<),g(p<<|));

}

int main()

{

    //freopen("1.in","r",stdin);

    n=read();m=read();

    for(int i=;i<=n;++i)b[i]=read(),a[i]=read();

    build(,,n);f[]=;flag=;

    for(int i=;i<=n;++i)

    {

        cnt+=a[i];

        while(cnt>m)++flag,cnt-=a[flag-];

        change(,flag-,i-,b[i]);

        f[i]=ask(,flag-,i-);

        //cout<<f[i]<<' ';

        if(i!=n)insert(,i);

    }

    put(f[n]);

    return ;

}

复杂度的证明：对于一个值各不相同的区间第一次肯定是暴力覆盖 然后变成了一个单调递减的 这样的话下一次修改一部分是直接区间覆盖了，一部分是跳过了跳过原因就是上述原因，然后均摊复杂度nlogn.很完美的解决了这种类型的dp优化。

2019 11 15 update：我再次 看了一下上述做法 有点没有必要 复杂度 有点假说实话一个绝佳的做法是利用单调栈 来维护 然后直接区间 修改即可。

单调栈 所以复杂度 是nlogn的 最多弹栈n次每次修改logn。上述做法 好像跟单调栈一样的好像qwq 好像直接忽略了 单调栈的存在 这样也行吧 复杂度都是 nlogn的 但是单调栈好理解。

什么垃圾set 优化 付了..

挥羽扇，整纶巾，少年鞍马尘。如今憔悴赋招魂，儒冠多误身。

记502 dp专练的更多相关文章

  1. 10-19 dp专练

    dp专练,终于克服了一次自己对dp的恐惧,磕出来一道题. 得分情况: T1:0 T2:0 T3:0 emmmm,磕出来的题是T2,但是因为初始化和int long long的原因爆零了 T1:n只狼排 ...

  2. dp专练

    dp练习. codevs 1048 石子归并 区间dp #include<cstdio> #include<algorithm> #include<cstring> ...

  3. DP 专练

    A - 跳蚤电话 观察性质,可以发现每次连边的点一定是有祖先关系的,可以直接挂上去一个,也可以是在中间边上插入一个点. 所以我很自然的想到去计算树上的点的加入顺序,因为一但加入顺序确定,每一次的操作也 ...

  4. HDOJ(HDU).4508 湫湫系列故事――减肥记I (DP 完全背包)

    HDOJ(HDU).4508 湫湫系列故事――减肥记I (DP 完全背包) 题意分析 裸完全背包 代码总览 #include <iostream> #include <cstdio& ...

  5. P1251 递推专练3

    递推专练3 描述 Description 圆周上有N个点.连接任意多条(可能是0条)不相交的弦(共用端点也算相交)共有多少种方案? 输入格式 Input Format 读入一个数N.<=N< ...

  6. 数位dp小练

    最近刷题的同时还得填填坑,说来你们也不信,我还不会数位dp. 照例推几篇博客: 数位DP讲解 数位dp 的简单入门 这两篇博客讲的都很好,不过代码推荐记搜的形式,不仅易于理解,还短. 数位dp的式子一 ...

  7. Solution -「树上杂题？」专练

    主要是记录思路,不要被刚开始错误方向带偏了 www 「CF1110F」Nearest Leaf 特殊性质:先序遍历即为 \(1 \to n\),可得出:叶子节点编号递增或可在不改变树形态的基础上调整为 ...

  8. HDU4526威威猫系列故事——拼车记（DP）

    http://acm.hdu.edu.cn/showproblem.php?pid=4526 额..七夕快乐哦 刚推的时候有点乱 又各种小错误 查了好久.. dp[i][k] = min(dp[i-1 ...

  9. [大山中学dp常练-4 Rounds]

    Round#1 2016.9.28 这次晚练十分sb 有点浪费时间 全是dp题 先说过程 3分钟草了第一题之后感觉好像有点水 然后翻了翻题目 看了看第一第四题两颗星 其他三颗星 然后一下子第二题题目太 ...

随机推荐

  1. 3.第一个scrapy项目

    第一个scrapy项目 1. 创建scrapy项目 1.1 创建项目三剑客 这里的三剑客指的是:创建项目以及运行项目的三条命令 1.1.1 创建项目 scrapy stratproject 项目名称 ...

  2. 【学习】从.txt文件读取生成编译代码。

    string code = null; String projectName = Assembly.GetExecutingAssembly().GetName().Name; // 1. 生成要编译 ...

  3. WPF DataGrid ScrollBar Style

    效果图如下 代码 <DataGrid.Resources> <Style TargetType="{x:Type ScrollBar}"> <Sett ...

  4. day39 作业

    实现生产消费原理 from multiprocessing import Process,JoinableQueue import time import random def cooker(q): ...

  5. 电商项目app开发

    购物app的开发 首先我们本次要写的是一个电商的项目,项目主要功能有登录.注册.商品展示.轮播图.加入购物车.购物车管理.支付管理.地址管理.个人信息的修改.商品的分类展示.微信支付等等.主要使用vu ...

  6. requests接口自动化3-url里带参数的get请求：params

    url里带参数的get请求:用params传参 #2.带参数的get请求,把参数写成字典格式,用params传参 para2={"type":"math"} r ...

  7. ASP.NET Core端点路由 作用原理

    端点路由(Endpoint Routing)最早出现在ASP.NET Core2.2,在ASP.NET Core3.0提升为一等公民. Endpoint Routing的动机 在端点路由出现之前,我们 ...

  8. accpet和connect设置超时

    三次握手 TCP连接建立的开始是三次握手,通过三次交互确认连接成功,在客户端调用connect时,客户端发送sync消息给服务端,服务端收到sync消息后,返回一个ack+sync,并等待ack,客户 ...

  9. 深入了解PHP的生成器

    在驾驶方面,速度并不会决定一切.但是在网络上,速度至关重要.你的应用程序越快,用户体验就越好.好吧,这时候有人就奇怪了,本文是关于PHP 生成器的,那么为什么我们要谈论速度呢?很快你就会发现,生成器在 ...

  10. [日常摘要] -- ThreadLocal篇

    简介 ThreadLocal,即线程变量,是一个以ThreadLocal对象为键.任意对象为值的存储结构.这个结构被附带在线程上,也就是说一个线程可以根据一个ThreadLocal对象查询到绑定在这个 ...