7.3 NOI模拟赛 苹果 随机 高维前缀和

头一次遇到高维前缀和的题目 所以赛时不太会写。

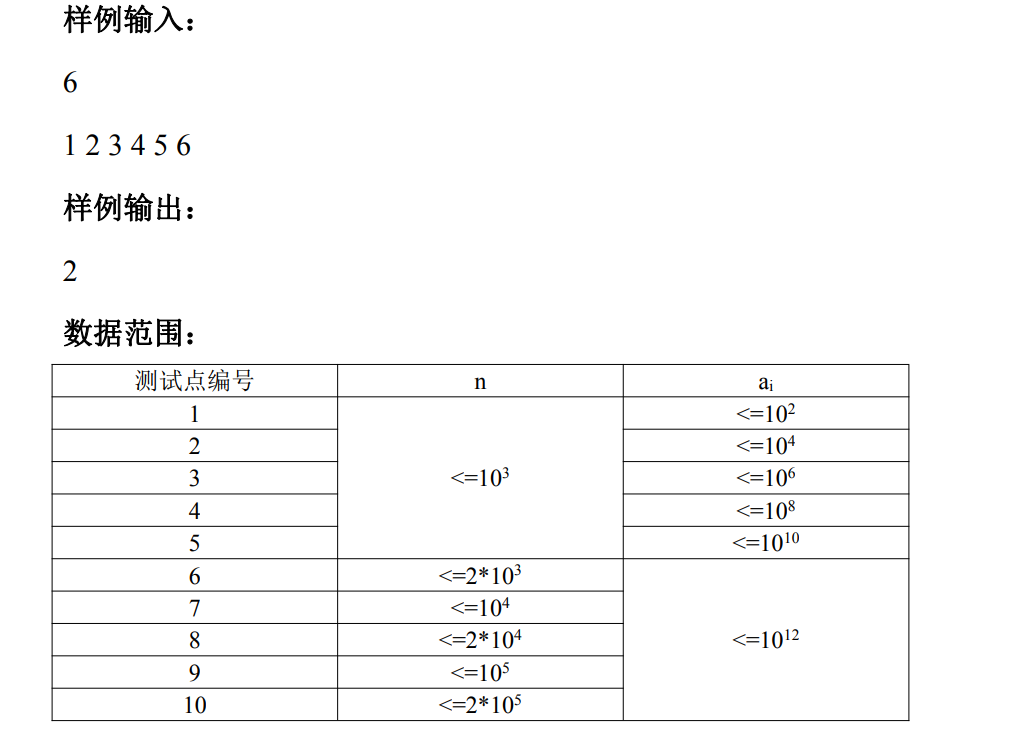
\(n\cdot Mx\cdot log\)的暴力做法这里不再赘述。

容易想到随机一个数字 然后其有\(\frac{1}{2}\)的概率在答案的集合中。

如果在答案集合中枚举这个数字的所有因子那么其中的一个就是答案 判定是这个因子的倍数的个数有多少个即可。

随机k次错误的概率为\(\frac{1}{2^k}\)所以正确性还是很稳的。

考虑如何进行判定 可以将所有数字和当前数字取gcd 然后gcd的那个数字的所有因数都可以加1.

利用高维前缀和 把p当做维度做就行了。

code bf:

//#include<bits\stdc++.h>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<queue>
#include<deque>
#include<stack>
#include<vector>
#include<algorithm>
#include<utility>
#include<bitset>
#include<set>
#include<map>
#define ll long long
#define db double
#define INF 1000000000
#define ldb long double
#define pb push_back
#define put_(x) printf("%d ",x);
#define get(x) x=read()
#define gt(x) scanf("%d",&x)
#define gi(x) scanf("%lf",&x)
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define gc(a) scanf("%s",a+1)
#define rep(p,n,i) for(RE int i=p;i<=n;++i)
#define go(x) for(int i=lin[x],tn=ver[i];i;tn=ver[i=nex[i]])
#define fep(n,p,i) for(RE int i=n;i>=p;--i)
#define vep(p,n,i) for(RE int i=p;i<n;++i)
#define pii pair<int,int>
#define mk make_pair
#define RE register
#define P 1000000007
#define gf(x) scanf("%lf",&x)
#define pf(x) ((x)*(x))
#define uint unsigned long long
#define ui unsigned
#define EPS 1e-9
#define sq sqrt
#define S second
#define F first
#define op(x) t[x].op
#define d(x) t[x].d
#define Set(a,v) memset(a,v,sizeof(a))
#define pf(x) ((x)*(x))
#define mod 19991207
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    RE int x=0,f=1;RE char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
const int MAXN=200010;
int n,cnt,ans=1;
int vis[MAXN],a[MAXN];
inline void check(int x)
{
	if(x<=ans)return;
	int cnt=0;
	rep(1,n,i)
	{
		if(a[i]%x==0)++cnt;
		if(n-i+cnt<n/2)return;
	}
	if(cnt>=n/2)ans=x;
}
inline void solve(int x)
{
	for(int i=2;i*i<=x;++i)
	{
		if(x%i==0)
		{
			check(i);
			if(x/i!=i)check(x/i);
		}
	}
}
int main()
{
	freopen("apple.in","r",stdin);
	freopen("apple.out","w",stdout);
	db st=clock();
	get(n);srand(time(0));
	rep(1,n,i)get(a[i]);
	while(clock()-st<900)
	{
		int x=rand()%n+1;
		if(vis[x])continue;
		vis[x]=1;solve(a[x]);
	}
	put(ans);
	return 0;
}

code sol:

//#include<bits\stdc++.h>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<queue>
#include<deque>
#include<stack>
#include<vector>
#include<algorithm>
#include<utility>
#include<bitset>
#include<set>
#include<map>
#define ll long long
#define db double
#define INF 1000000000
#define ldb long double
#define pb push_back
#define put_(x) printf("%d ",x);
#define get(x) x=read()
#define gt(x) scanf("%d",&x)
#define gi(x) scanf("%lf",&x)
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define gc(a) scanf("%s",a+1)
#define rep(p,n,i) for(RE ll i=p;i<=n;++i)
#define go(x) for(ll i=lin[x],tn=ver[i];i;tn=ver[i=nex[i]])
#define fep(n,p,i) for(RE ll i=n;i>=p;--i)
#define vep(p,n,i) for(RE ll i=p;i<n;++i)
#define pii pair<ll,ll>
#define mk make_pair
#define RE register
#define P 1000000007
#define gf(x) scanf("%lf",&x)
#define pf(x) ((x)*(x))
#define uint unsigned long long
#define ui unsigned
#define EPS 1e-9
#define sq sqrt
#define S second
#define F first
#define op(x) t[x].op
#define d(x) t[x].d
#define Set(a,v) memset(a,v,sizeof(a))
#define pf(x) ((x)*(x))
#define mod 19991207
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline ll read()
{
    RE ll x=0,f=1;RE char ch=getc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
    return x*f;
}
const ll MAXN=200010;
ll n,cnt,top;
ll vis[MAXN];
ll a[MAXN],p[MAXN],s[MAXN],L[MAXN],R[MAXN],ans=1;
map<ll,ll>H;
inline ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
inline void solve(ll x)
{
	if(x<=ans)return;
	H.clear();cnt=0;top=0;ll ww=x;
	for(ll i=1;i*i<=x;++i)
	{
		if(x%i==0)
		{
			s[++cnt]=i;
			if(x/i!=i)s[++cnt]=x/i;
			if(ww%i==0&&i!=1)
			{
				p[++top]=i;
				while(ww%i==0)ww/=i;
			}
		}
	}
	if(ww>1)p[++top]=ww;
	rep(1,n,i)++H[gcd(a[i],x)];
	rep(1,top,i)
	{
		ww=x/p[i];ll w1=0,w2=0;
		for(ll j=1;j*j<=ww;++j)
		{
			if(ww%j==0)
			{
				L[++w1]=j;
				if(ww/j!=j)R[++w2]=ww/j;
			}
		}
		rep(1,w2,j)H[R[j]]+=H[R[j]*p[i]];
		fep(w1,1,j)H[L[j]]+=H[L[j]*p[i]];
	}
	rep(1,cnt,i)
	{
		if(s[i]>ans)if(H[s[i]]>=n/2)ans=s[i];
	}
}
signed main()
{
	freopen("apple.in","r",stdin);
	freopen("apple.out","w",stdout);
	db st=clock();
	get(n);srand(time(0));
	rep(1,n,i)get(a[i]);ll cc=0;
	while(clock()-st<900&&cc<=10)
	{
		ll x=rand()%n+1;
		if(vis[x])continue;
		vis[x]=1;solve(a[x]);++cc;
	}
	put(ans);//put(cc);
	return 0;
}