树链剖分详解&题解 P6098 【[USACO19FEB]Cow Land G】

看到各位大佬们已经把其他的东西讲的很明白了，我这个 juruo 就讲一讲最基本的树链剖分吧。

0.树剖是什么？能吃吗？

不能吃

树剖是树链剖分的简称，我们一般说的树剖其实指重链剖分。当然，还有一种长链剖分我不会，但是据说不常用。

树链剖分能够把树剖分成许多链，这样就可以用维护区间的方式维护一棵树。

1.怎么剖分

先引入一些概念：

重儿子：一棵树最大的子树叫重儿子。例如这棵树中3就是1的重儿子：很明显，一棵树的重儿子是唯一的。什么？有多棵子树的大小相同？那就随便选一个呗。
轻儿子：除了重儿子都是轻儿子。废话
重边：连接父亲和重儿子的边就是重边。
轻边：除了重边都是轻边。
重链：许多重边连起来就叫重链。例如：

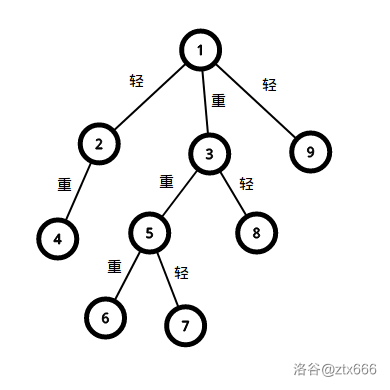
这棵树里节点 $\{1,3,5,6\}$ 可以构成一颗重链。很显然，每个重链的起点一定是一个轻儿子。每个节点都属于且仅属于一条重链。<-很重要，一定要记住！

然后就开始剖分了。

具体的剖分过程，就是维护一些数组：

$deep[i]$ 代表节点 $i$ 的深度。
$top[i]$ 代表节点 $i$ 所属重链的链顶。（也就是重链里深度最小的那个节点）
$size[i]$ 代表以 $i$ 为根的子树的大小。
$son[i]$ 代表节点 $i$ 的唯一一个重儿子是谁。
$f[i]$ 代表节点 $i$ 的父亲是谁。
$dfn[i]$ 代表节点 $i$ 的”遍历顺序“。

剖分时要跑两个dfs。经典操作

第一个dfs要维护 $size$ 、$son$ 、$f$、$deep$ 这几个数组。

提示：树要用无向图存！

void dfs1(int u,int fa/*记录当前节点父亲是谁*/){
    size[u]=1;//因为自己也是子树的一部分
    f[u]=fa;
    deep[u]=deep[fa]+1;//很明显，当前深度=父亲深度+1
    for(int i=0;i<g[u].size();i++){
        int v=g[u][i];//遍历每个出边
        if(v!=fa){//如果当前出边终点是儿子而不是父亲
            dfs1(v,u);//搜
            size[u]+=size[v];//加上儿子大小
            if(size[v]>size[son[u]]){//找到最大的儿子作为重儿子
                son[u]=v;
            }
        }
    }
}

然后我们已经知道了每个节点的重儿子，现在应该把它们连起来成为一条重链了：

void dfs2(int u,int tp/*当前链顶*/){
    top[u]=tp;
    dfn[u]=++step;
    if(son[u]){//如果没有重儿子，那么一个儿子也没有
        dfs2(son[u],tp);//优先遍历重儿子，为什么之后再说
        for(int i=0;i<g[u].size();i++){
            int v=g[u][i];
            if(son[u]!=v&&f[u]!=v){//遍历轻儿子
                dfs2(v,v);//轻儿子一定是一条重链的链顶
            }
        }
    }
}

如果优先遍历重儿子，那么重链的$dfn$一定是连续的。例如：

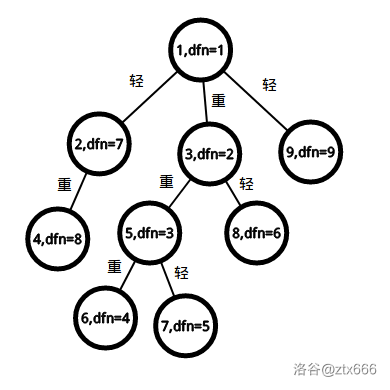
因为重链的$dfn$是连续的，而每个点都属于一条重链，所以可以用线段树维护区间的方式维护点权，这样就不用暴力的一个个查，一个个改了。

一些常见的用法：

query(1,1,n,dfn[top[u]],dfn[u])//查询u到链顶的点权和
modify(1,1,n,dfn[top[u]],dfn[u],3)//把u到链顶的点权都加3

具体到题目上，可以发现甚至连懒惰标记都不需要，没有区间修改的操作。

那么，怎么计算从一个点到另外一个点路径上的点权和？

int query_ans(int u,int v){
    int ret=0;
    while(top[u]!=top[v]){
        if(deep[top[u]]<deep[top[v]]){//注意，一定要比较链顶深度！坑了我好几次
            swap(u,v);
        }
        ret^=query(1,1,n,dfn[top[u]],dfn[u]);//这道题要求异或
        u=f[top[u]];
    }//就是当uv不在同一条链上时，让链顶深度小的往上跳
    if(deep[u]>deep[v]){
        swap(u,v);
    }
    ret^=query(1,1,n,dfn[u],dfn[v]);//当在同一条链上时，把它们之间的点加起来
    return ret;
}

知道了这些操作，这题就非常好写了。就是直接把板子套上去嘛！

AC Code：

#include <bits/stdc++.h>
using namespace std;
#define MAXN 200005
int n,q,e[MAXN];
vector<int> g[MAXN];
int dfn[MAXN],step,top[MAXN],size[MAXN],son[MAXN],f[MAXN],deep[MAXN];
void dfs1(int u,int fa){
    size[u]=1;
    f[u]=fa;
    deep[u]=deep[fa]+1;
    for(int i=0;i<g[u].size();i++){
        int v=g[u][i];
        if(v!=fa){
            dfs1(v,u);
            size[u]+=size[v];
            if(size[v]>size[son[u]]){
                son[u]=v;
            }
        }
    }
}
void dfs2(int u,int tp){
    top[u]=tp;
    dfn[u]=++step;
    if(son[u]){
        dfs2(son[u],tp);
        for(int i=0;i<g[u].size();i++){
            int v=g[u][i];
            if(son[u]!=v&&f[u]!=v){
                dfs2(v,v);
            }
        }
    }
}
int tree[MAXN*4];
void push_up(int rt){
    tree[rt]=tree[rt*2]^tree[rt*2+1];
}
void modify(int rt,int l,int r,int x,int k){
    if(l==r){
        tree[rt]=k;
    }else{
        int mid=(l+r)/2;
        if(x<=mid){
            modify(rt*2,l,mid,x,k);
        }else{
            modify(rt*2+1,mid+1,r,x,k);
        }
        push_up(rt);
    }
}
int query(int rt,int l,int r,int L,int R){
    if(L>R){return 0;}
    if(L<=l&&R>=r){
        return tree[rt];
    }else{
        int mid=(l+r)/2,ret=0;
        if(L<=mid){
            ret^=query(rt*2,l,mid,L,R);
        }
        if(R>mid){
            ret^=query(rt*2+1,mid+1,r,L,R);
        }
        return ret;
    }
}
int query_ans(int u,int v){
    int ret=0;
    while(top[u]!=top[v]){
        if(deep[top[u]]<deep[top[v]]){
            swap(u,v);
        }
        ret^=query(1,1,n,dfn[top[u]],dfn[u]);
        u=f[top[u]];
    }
    if(deep[u]>deep[v]){
        swap(u,v);
    }
    ret^=query(1,1,n,dfn[u],dfn[v]);
    return ret;
}
int main(){
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++){
        scanf("%d",e+i);
    }
    for(int i=1;i<=n-1;i++){
        int u,v,w;
        scanf("%d%d",&u,&v);
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs1(1,0);
    dfs2(1,1);
    for(int i=1;i<=n;i++){
        modify(1,1,n,dfn[i],e[i]);
    }
    for(int i=1;i<=q;i++){
        int op;
        scanf("%d",&op);
        if(op==1){
            int x,k;
            scanf("%d%d",&x,&k);
            modify(1,1,n,dfn[x],k);
        }else{
            int u,v;
            scanf("%d%d",&u,&v);
            printf("%d\n",query_ans(u,v));
        }
    }
    return 0;
}

完结撒花~