UVA11300 Spreading the Wealth 题解

题目

A Communist regime is trying to redistribute wealth in a village. They have have decided to sit everyone around a circular table. First, everyone has converted all of their properties to coins of equal value, such that the total number of coins is divisible by the number of people in the village. Finally, each person gives a number of coins to the person on his right and a number coins to the person on his left, such that in the end, everyone has the same number of coins. Given the number of coins of each person, compute the minimum number of coins that must be transferred using this method so that everyone has the same number of coins.

一个村庄重新分配财富。 他们已经决定让每个人围坐在一张圆桌旁。 首先，每个人都将其所有财产转换为等值的硬币，这样硬币的总数就可被村庄中的人数整除。 最后，每个人都给右边的人一些硬币，给左边的人一些硬币，每个人都有相同数量的硬币。 给定每个人的硬币数量，计算必须使用此方法转移的最小硬币数量，以便每个人都拥有相同数量的硬币。

输入格式

There is a number of inputs. Each input begins with \(n (n < 1000001)\), the number of people in the village. n lines follow, giving the number of coins of each person in the village, in counterclockwise order around the table. The total number of coins will fit inside an unsigned 64 bit integer.

有多组输入。 每个输入均以数字\(n（n <1000001）\)开头，即人数.接下来\(n\)行，以逆时针方向给出村庄中每个人的硬币数量。 硬币总数将是一个无符号的64位整数。

输出格式

For each input, output the minimum number of coins that must be transferred on a single line.

对于每组输入，输出转移的最小硬币数。

输入样例

3
100
100
100
4
1
2
5
4

输出样例

0
4

题解

这道题感觉有点像数学题啊

因为一个人只能左右传硬币,所以只需要考虑左右

而每个人最开始的硬币数和最终的硬币数都是已知的,所以列方程即可

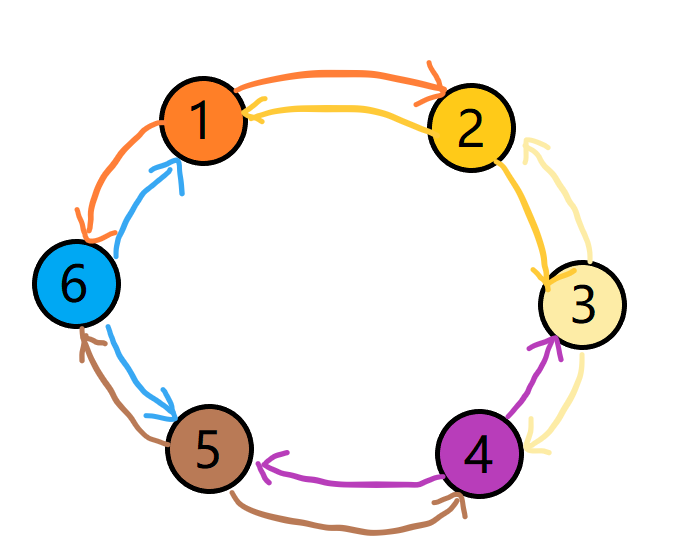
设\(coin_i\)为最开始每个人的硬币数量,\(pass_i\)为第\(i\)个人给逆时针方向的人(\(i-1\))的硬币数量,\(x\)为最终每个人的硬币数量.

这时候可能有的人就会疑惑了,为啥只给逆时针方向的人不给顺时针方向的人?

我们假设一下,\(1\)号给\(2\)号\(5\)个硬币,\(2\)号给\(1\)号\(3\)个硬币,一共转移了\(8\)个硬币,何必这么麻烦?直接让\(1\)号给\(2\)号\(2\)个硬币不就得了? 这样只需要转移\(2\)个硬币了.

注意,这个硬币数量可以是负数,也就是说,\(1\)号给\(6\)号\(-2\)个硬币,相当于6号给1号\(2\)个硬币

所以,相邻两人之间只会有一次硬币转移.

那我们擦去顺时针的:

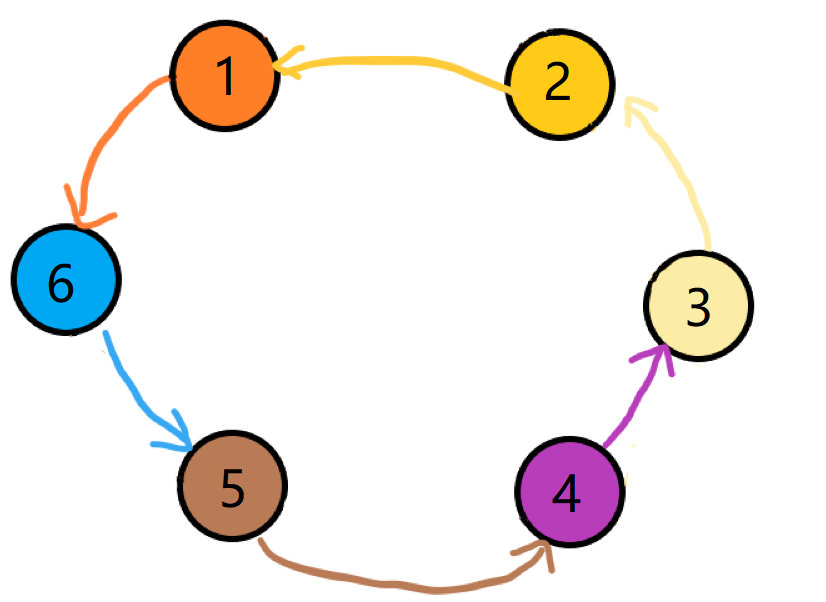
然后就可以开始列式子了:

\(x=coin_1+pass_2-pass_1\)

\(x=coin_2+pass_3-pass_2\)

\(\dots\)

\(x=coin_n+pass_1-pass_n\)

移项

\(pass_2=x-coin_1+pass_1\)

\(pass_3=x-coin_2+\bm{pass_2}
\\ \ \ \ \ \ \ \ \ \ \ = x-coin_2+\bm{x_1-coin_1+pass_1}
\)

\(\dots\)

由题意,我们应该让\(\sum_{i=1}^n pass_i\)最小

为了方便描述,再设一个数组\(b_i\),使\(b_0=0\),\(b_i=coin_i+b_{i-1}-x\)

这样就可以方便的表示\(pass_i\),再表示一遍

\(pass_2=pass_1+x-coin_1
\\ \ \ \ \ \ \ \ \ \ \ = pass_1 - (coin_1-x)
\\ \ \ \ \ \ \ \ \ \ \ = pass_1 - b_1
\)

\(pass_3=\bm{pass_2}+x-coin_2
\\ \ \ \ \ \ \ \ \ \ \ = \bm{pass_1 - b_1} +x - coin_2
\\ \ \ \ \ \ \ \ \ \ \ = pass_1 - (\bm{coin_2+b_1-x})
\\ \ \ \ \ \ \ \ \ \ \ = pass_1 - \bm{b_2}
\)

\(\dots\)

所以

\(\sum_{i=1}^npass_i = pass_1+pass_2+pass_3+\dots+pass_n
\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = |pass_1 - b_1|+|pass_1 - b_2| + \dots + |pass_1 - b_{n-1}|
\)

注意,这个式子相当于数轴上\(b_1,b_2,b_3,b_4\cdots\)到\(pass_1\)的距离之和,那么使这个距离之和最小即可

这里我们可以就用中位数的性质了:

在数轴上所有n个点中，中位数离所有点的距离之和最小

求出最小的和输出即可

理解

对于这个数轴,中位数为2,与其他点距离的和为6

如果不选择中位数,比如选择1,那么与其他点距离的和为7

形象的理解,当\(pass_1\)向左移动一个单位长度时,虽然有两个点的距离缩小了\(d\),但是有3个点的距离增加了\(d\),显然结果变大

若移动两个单位长度,同理结果大于移动一个单位长度,所以当选择中位数时,结果最小.

如果出现偶数个点,

\([2,3]\)中任意一个点皆可做\(pass_1\),由于\(pass_1\)为整数并且为了写代码方便,取端点值即可

证明

1. 给定一个从小到大的数列\(x_1,x_2,\dots x_n\)

2. 设\(x\)是从\(x1\)到\(x_n\)与其绝对差之和最小的数.

3. 当\(x\)在\(x_1\)与\(x_n\)之间,\(x\)与\(x_1\),\(x_n\)的距离和就是\(x_1\)到\(x_n\)的距离,
   
   若不在\(x_1\)与\(x_n\)之间,\(x\)与\(x_1\),\(x_n\)的距离和还要额外加上一段,
   
   则\(x\)位于\(x_1\)与\(x_n\)之间.

4. 由于\(x_1, x_n\)与它们之间的任意一点的距离之和(\(|x_i-x_1|+ |x_i- x_n\)|)都相等，等于\(x_n一x_1\)，因此不需要考虑\(x_1, x_n\).

5. 由第3点可得,\(x\)位于\(x_2\)与\(x_{n-1}\)之间,且\(x\)与\(x_2,x_{n-1}\)的距离和相等,不需要考虑.

6. 依次类推，\(x\)就是该数列中间的那个数，或者是中间的那两个数之一， 而这个数就是中位数.

代码

#include <algorithm>
#include <cstdio>
using namespace std;
const int maxn = 1000000 + 10;
long long coin[maxn], b[maxn], tot, x;
int main() {
    int n;
    while (~scanf("%d", &n)) {
        tot = b[0] = 0;
        for (int i = 1; i <= n; i++) {
            scanf("%lld", &coin[i]);
            tot += coin[i];
        }
        x = tot / n;
        for (int i = 1; i < n; i++) b[i] =  coin[i] + b[i - 1] - x;
        sort(b, b + n);
        long long mid = b[n / 2], ans = 0;
        for (int i = 0; i < n; i++) ans += abs(mid  - b[i]);
        printf("%lld\n", ans);
    }
    return 0;
}