蓝桥杯大学B组省赛2020模拟赛（一）题解与总结
题目链接：https://www.jisuanke.com/contest/6516
A：题目：
我们称一个数是质数,而且数位中出现了 5 的数字是有趣的。
例如 5, 59, 457。求1到100000中有趣的数的个数。
题解:无脑分解和暴力枚举素数即可。
代码：
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long ll;
const int mod = ;
bool check(int x)
{
int flag = ;
for (int i = ; i <= sqrt(x); i++)
if (x % i == )
flag = ;
if (flag == )return false;
else return true;
}
bool check2(int x)
{
int t;
while (x != )
{
t = x % ;
x = x / ;
if (t == )return true;
}
return false;
}
int main(void)
{
int num = ;
for (int i = ; i <= ; i++)
{
if (check(i) == true)
if (check2(i) == true)
num++;
}
cout << num << endl;
return ;
}
答案：3282
B：题目：
蒜头君要爬楼梯。楼梯一共有10层台阶。
因为腿长的限制，每次最多能上4层台阶。但是第5,7层楼梯坏掉了不能踩。求上楼梯的方案数。
题解：通过上一层转移，没啥坑。
代码：
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
typedef long long ll;
const int mod = ;
int dp[];
int main(void)
{
dp[] = ;
dp[] = dp[] + ;
dp[] = dp[] + dp[] + ;
dp[] = dp[] + dp[] + dp[] + ;
dp[] = ;
dp[] = dp[] + dp[] + dp[] + dp[];
dp[] = ;
for (int i = ; i <= ; i++)
dp[i] = dp[i - ] + dp[i - ] + dp[i - ] + dp[i - ];
cout << dp[] << endl;
return ;
}
答案：72
C：题目：求问在以下图案的大三角形内部添加五条直线最多可以将大三角形分成多少个区域。
请在下图的基础上添加五条直线。
题解：
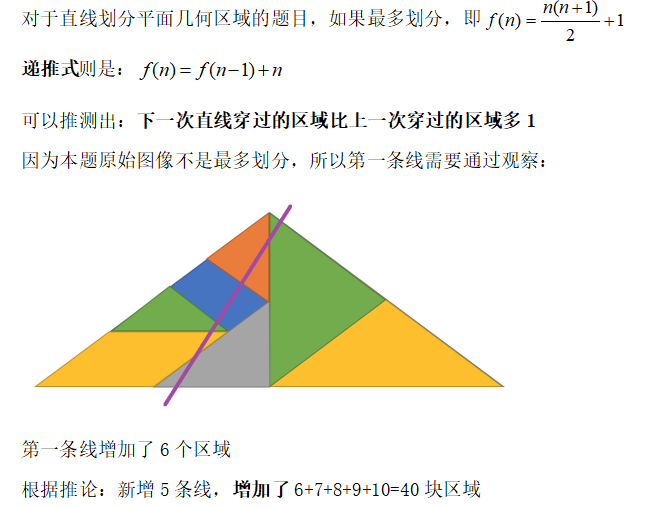
答案：47
D：题目：
有3030个篮子，每个篮子里有若干个苹果，篮子里的苹果数序列已经给出。
现在要把苹果分给小朋友们，每个小朋友要么从一个篮子里拿三个苹果，要么从相邻的三个篮子里各拿一个苹果。（苹果可以剩余）
比如对于序列3 1 3，可以分给两个小朋友变成0 1 0；也可以分给一个小朋友变成2 0 2，此时不能继续再分了。所以答案是2。
求问对于以下序列{7,2,12,5,9,9,8,10,7,10,5,4,5,8,4,4,10,11,3,8,7,8,3,2,1,6,3,9,7,1}最多分给几个小朋友？
题解：本题考虑贪心，贪心的策略是：从左到右取苹果，使浪费的苹果最少。篮子中大于等于3个苹果的直接取3个，取到小于3个为止。然后将此篮子当作1 1 1取法的左端点，继续取，直到无法操作。
这样确保每次都是局部最优，因而推出整体最优。
代码：
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
//尽可能少剩下的苹果最少为贪心思路
int main()
{
ios::sync_with_stdio(false);
int sum = ;
int a[] = { ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, };
int ans = ;
for (int i = ; i <= ; ++i)
{
ans += a[i] / ;
a[i] %= ;
/*
for (int i = 1; i <= 30; i++)
cout << a[i] << " ";
cout << endl;
*/
while (a[i] >= && a[i + ] >= && a[i + ] >= )
{
a[i]--; a[i + ]--; a[i + ]--;
ans++;
}
}
cout << ans << endl;
return ;
}
答案：62
E：题目：
广场上的小朋友们排成了整齐的方阵。具体来说，我们可以把每个小朋友看做是一个点，那么小朋友们就形成了n×n的点阵。
方阵中，小朋友A和小朋友B互相可以看见，当且仅当二人之间的连线不经过别的小朋友，且他们之间的距离不超过k。我们想知道有多少对小朋友互相可以看见。(A,B)与 (B,A)算同一对。
例如，n=2,k=1时答案为4，n=2,k=2 时答案为6，n=3,k=2时答案为20。
现在我们想要知道，当n=1000,k=500时的答案是多少。由于答案过大，请回答对10^9+7取模后的结果。
分析：本题是填空题中唯一有难度的一问，坑点较多。（ps：用了对拍才找到自己的错误）
题解：
代码：（正确代码）
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD = 1e9 + ;
int main()
{
int n, k;
cin >> n >> k;
ll ans = * n * (n - ) % MOD;//边框上的线数目
for(int x = ; x <= n; x++)
{
for(int y = ; y <= n; y++)
{
if(x * x + y * y > k * k)continue;
if(__gcd(x, y) != )continue;
ans = (ans + * (n - x) * (n - y)) % MOD;
}
}
cout<<ans;
return ;
}
解释：对于代码中ans的解释
暴力对拍代码：（直接跑可能要3000s才能出答案）
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD = 1e9 + ;
int main()
{
int n, k, ans = ;
cin >> n >> k;
///第一个点(sx, sy) 第二个点(tx, ty)
for(int sx = ; sx <= n; sx++)
{
for(int sy = ; sy <= n; sy++)
{
for(int tx = ; tx <= n; tx++)
{
for(int ty = ; ty <= n; ty++)
{
if(sx == tx && sy == ty)continue;
if((tx - sx) * (tx - sx) + (ty - sy) * (ty - sy) > k * k)continue;
if(__gcd(abs(tx - sx), abs(ty - sy)) != )continue;
ans++;
}
}
}
}
cout<<ans / ;
return ;
}
答案：916585708
F：题目：
题解：直接用map或者set存即可，数据范围不大，不会mle或者tle。
坑点：要把a0=1提前存入，不然就会只有13/15分。（别问为啥知道，问就是白给）
代码：
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <map>
using namespace std;
typedef long long ll;
const int mod = ;
ll A, B, C;
int a[];
map<int, int>m;
int main(void)
{
cin >> A >> B >> C;
int flag = ;
a[] = ;
m[] = ;
for (int i = ; i <= ; i++)
{
a[i] = (A * a[i - ] + a[i - ] % B) % C;
if (m[a[i]] == )
m[a[i]]++;
else
{
cout << i << endl;
return ;
}
}
cout << "-1" << endl;
return 0;
}
G：题目：
分析：一道稍微有点繁琐，题面有错的模拟。
输出的第一行，应该是被破坏的道路，房屋，田地的总数。（十分的蛋疼，比赛的时候完全按照题面只有2/20分）
注意：
①溅射伤害是高级炮弹击中的k*k区域的每一小块周围的8小块都会受到的伤害。
②该开long long的地方不要吝啬。
代码：（按照修改后的题意）
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <map>
using namespace std;
typedef long long ll;
const int mod = ;
const int maxn = ;
ll blood[];//三种血量
ll sum[];//三种受的伤
int mp[maxn][maxn];//编号地图
ll now[maxn][maxn];//血量地图
ll hurt[maxn][maxn];//基本伤害
int dx[] = { ,,,-,,,-,- };
int dy[] = { ,-,,,,-,,- };
int main(void)
{
ios::sync_with_stdio(false);
int n, m; cin >> n >> m;
cin >> blood[] >> blood[] >> blood[];
int k; ll w;//范围与溅射伤害
cin >> k >> w;
for (int i = ; i <= k; i++)
for (int j = ; j <= k; j++)
cin >> hurt[i][j];
for (int i = ; i <= n; i++)
for (int j = ; j <= m; j++)
{
cin >> mp[i][j];
now[i][j] = blood[mp[i][j]];
}
//计算攻击
int q; cin >> q;
while (q--)
{
int op, x, y;
cin >> op >> x >> y;//爆炸中心x y
int s1, s2, e1, e2;
s1 = max(, x - k / );//行开始
e1 = min(n, x + k / );//行结束
s2 = max(, y - k / );//列开始
e2 = min(m, y + k / );//列结束
for (int i = s1; i <= e1; i++)
{
for (int j = s2; j <= e2; j++)
{
int ii = (i - x) + (k + ) / ;//相对中心点的位置
int jj = (j - y) + (k + ) / ;
if (now[i][j] > )//在受到炸弹之前还有血
{
sum[mp[i][j]] += min(now[i][j], hurt[ii][jj]);
now[i][j] -= hurt[ii][jj];
if (now[i][j] < )
now[i][j] = ;
}
if (op == )//若有溅射伤害
{
for (int f = ; f < ; f++)
{
int i_new = i + dx[f];
int j_new = j + dy[f];
if (i_new< || i_new>n || j_new< || j_new>m) continue;
if (now[i_new][j_new] > )//在受到溅射之前还有血
{
sum[mp[i_new][j_new]] += min(now[i_new][j_new], w);
now[i_new][j_new] -= w;
if (now[i_new][j_new] < )
now[i_new][j_new] = ;
}
}
}
}
}
}
int ans[] = { };
for (int i = ; i <= n; i++)
for (int j = ; j <= m; j++)
ans[mp[i][j]] += (now[i][j] == );
cout << ans[] << " " << ans[] << " " << ans[] << endl;
cout << sum[] + sum[] + sum[] << endl;
return ;
}
H：题目：
分析：如果按位展开，每次都暴力计算判断是否乘除的话，必然拿不到满分（强数据会tle）。
所以在计算是否整除的时候做了以下优化：
①第一次计算总和时，借助了已经打好的按位取模后的乘权表
②之后双重for循环找交换的两位字母，在取模环境下，减去两个换前原字母所对应的值，加上两个换后字母对应的值进行O(1)的更新判断。
可行性分析：在无除法的运算过程中，加法和乘法的同余模定理确保了对每一步都取模后的结果不会让最后的答案不变。
代码：
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <cstring>
using namespace std;
typedef long long ll; ll f[];///f[i] = 26^i % M
int main(void)
{
string s;
cin >> s;
ll M;
cin >> M;
f[] = % M;
int n = s.size();
for (int i = ; i <= n; i++)
f[i] = f[i - ] * % M; ll sum = ;
for (int i = ; i < n; i++)
sum = (sum + f[n - - i] * (s[i] - 'A')) % M;
if (sum == )
{
cout << "0 0" << endl;
return ;
}
else
{
for (int i = ; i < s.size(); i++)
{
for (int j = i + ; j < s.size(); j++)
{
ll tmp = sum;
tmp = ((tmp - f[n - - i] * (s[i] - 'A')) % M + M) % M;
tmp = ((tmp - f[n - - j] * (s[j] - 'A')) % M + M) % M;
tmp = ((tmp + f[n - - i] * (s[j] - 'A')) % M + M) % M;
tmp = ((tmp + f[n - - j] * (s[i] - 'A')) % M + M) % M;
if (tmp == )
{
cout << i + << " " << j + << endl;
return ;
}
}
}
}
cout << "-1 -1" << endl;
return ;
}
注意：避免产生负数，取模之后的减法要加上模数，再取模确保计算结果为正。
I：题目：
分析：显然，这一题的数据不能一个点跑一次dijkstra。我们发现对于起点1到所有点的最短路，可以一次dijkstra完成。但如果此时，选择每一目的地出发，跑dijkstra，那需要再跑n-1次，显然不是明智的选择。
我们可以通过将边反存，这样所有从非起点指向1的边变成了1指向所有目的地。只要再dijkstra一次反向存边，便可计算出从目的地返回起点的最短路。
代码：
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <map>
#include <queue>
using namespace std;
typedef long long ll;
const int maxn = ;
const ll INF = 1e15;
struct edge
{
int v, w;///v表示终点 w表示边长
edge() {}
edge(int vv, int ww){v = vv;w = ww;}
};
struct Heapnode
{
int id;
ll d;///id表示节点的编号，d表示从s走到id的距离
Heapnode() {}
Heapnode(int id, ll d) :id(id), d(d) {}
bool operator <(const Heapnode& a)const
{
return d > a.d;
}
};
vector<edge>Map[][maxn];
int n, m;
///添加一条从u出发到v结束，边长为w的边
void addedge(int u, int v, ll w)
{
Map[][u].push_back(edge(v, w));
Map[][v].push_back(edge(u, w));///反向建图
}
ll d[][maxn];///d[i]表示从s出发，到达i的最短距离
bool vis[maxn];
void Dijkstra(int s, int id)
{
for (int i = ; i <= n; i++)d[id][i] = INF, vis[i] = ;
d[id][s] = ;
priority_queue<Heapnode>q;
q.push(Heapnode(s, ));
while (!q.empty())
{
Heapnode now = q.top();
q.pop();
int u = now.id;
if (vis[u])continue;
vis[u] = ;
for (int i = ; i < Map[id][u].size(); i++)
{
///u -> v 边长为w
int v = Map[id][u][i].v;
int w = Map[id][u][i].w;
if (d[id][u] + w < d[id][v])
{
d[id][v] = d[id][u] + w;
q.push(Heapnode(v, d[id][v]));
}
}
}
}
int main(void)
{
ios::sync_with_stdio(false);
int T;
cin >> T;
while (T--)
{
cin >> n >> m;
for (int i = ; i <= n; i++)
Map[][i].clear(), Map[][i].clear();
ll sum = ;
for (int i = ; i <= m; i++)
{
int u, v; ll w;
cin >> u >> v >> w;
addedge(u, v, w);
}
Dijkstra(, );
Dijkstra(, );
for (int i = ; i <= n; i++)
sum += d[][i] + d[][i];
cout << sum << endl;
}
return ;
}
注意：不确定数值大小的话，都用long long（除了恶心的多校之外，一般不会卡ll）；初始化的INF一定要大一些，如果使用0x3f3f3f3f会出错
J：题目：
分析：这是一题很棒的搜索题，题目中说确保每个点是至多是一个传送门的入口（仅仅只能说明传送门的出度是唯一的,即一个传送门对应一个目的地）
例如下图，
因此说明，传送门的传送位置是传送门；传送门死循环等状况也是可能的。
所以对于任意一点非障碍物a有以下情况：
（一）a是传送门
1：经过终点
2：传n次，落在合法位置
3：传n次，卡在障碍物
4：死循环
（二）a不是传送门
所以如果利用队列，我们需要将下一个即将压入队列的点进行预处理，才能当作正常bfs搜索操作。
难点处理：我们利用了map去映射传送门的起点对和终点对，写了函数Find_Next(a)去寻找点a进入传送门后的结果
1：正常情况：返回出口
2：卡在障碍物：返回-1,-1
3：死循环：返回-1,-1
4：只要经过终点：返回终点
代码：
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <map>
#include <queue>
#include <set>
using namespace std;
typedef long long ll;const int N = ;
const int inf = 0x3f3f3f3f;
char Mp[N][N];//地图
bool vis[N][N];//标记
int dx[] = { ,-,, };
int dy[] = { ,,,- };
int x, y;//目的地
int n, m;
typedef pair<int, int> Pair;
map<Pair, Pair>door;
struct node
{
int x, y, num;
node() {}
node(int xx, int yy, int nnum) { x = xx; y = yy; num = nnum; }
node(Pair a, int nnum)
{
x = a.first;
y = a.second;
num = nnum;
}
};
///a是传送门入口 返回传送门出口
///1：正常情况：返回出口
///2：卡在障碍物：返回-1,-1
///3：死循环：返回-1,-1
///4：只要经过终点：返回终点
Pair Find_Next(Pair a)
{
Pair start = a;
set<Pair>s;///走过的点全都塞入s中
while (true)
{
if (a.first == x && a.second == y)return make_pair(x, y);
if (Mp[a.first][a.second] == '*')return make_pair(-, -);
if (door.count(a))
{
if (s.count(a))return make_pair(-, -);
s.insert(a);
a = door[a];
}
else return a;
}
} int main()
{
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i = ; i <= n; i++)
cin >> (Mp[i] + );
int k;
cin >> k;
while (k--)
{
int a, b, c, d;
cin >> a >> b >> c >> d;
door[make_pair(a, b)] = make_pair(c, d);
}
cin >> x >> y;
Pair Start = make_pair(, );
if (Find_Next(Start).first == -)
{
cout << "No solution" << endl;
return ;
}
queue<node>q;
Start = Find_Next(Start);
q.push(node(Start, ));
vis[Start.first][Start.second] = ;
while (!q.empty())
{
node now = q.front();
q.pop();
if (now.x == x && now.y == y)
{
cout << now.num << endl;
return ;
}
for (int i = ; i < ; i++)
{
int xx = now.x + dx[i];
int yy = now.y + dy[i];
if (xx < || xx > n || yy < || yy > m)continue;
if (Mp[xx][yy] == '*')continue;
if (vis[xx][yy])continue;
Pair Next = Find_Next(make_pair(xx, yy));
//cout<<xx<<" "<<yy<<" "<<Next.first<<" "<<Next.second<<endl;
if (Next.first == -)continue;
q.push(node(Next, now.num + ));
vis[Next.first][Next.second] = ;
}
}
cout << "No solution" << endl;
return ;
}
Ps：题目数据似乎不强，没有涉及到传送门死循环的数据，但是处于严谨还是考虑上啦（毕竟补题）
蓝桥杯大学B组省赛2020模拟赛（一）题解与总结的更多相关文章
- (acwing蓝桥杯c++AB组）1.1 递归
(acwing蓝桥杯c++AB组)1.课程介绍+递归 文章目录 (acwing蓝桥杯c++AB组)1.课程介绍+递归 课程介绍 第一讲 递归与递推 递归 引入 递归的底层调用顺序 例题与练习 课程介绍 ...
- Java实现 第十一届 蓝桥杯 （本科组）省内模拟赛
有错误的或者有问题的欢迎评论 计算机存储中有多少字节 合法括号序列 无向连通图最少包含多少条边 字母重新排列 凯撒密码加密 反倍数 正整数的摆动序列 螺旋矩阵 小明植树 户户通电 计算机存储中有多少字 ...
- 2019第十届蓝桥杯C++B组题解（赛后重写的，不确保答案正确性，仅供参考）
先说一下这次的感受吧,我们考场比较乱,开始比赛了,还有的电脑有故障,(向这些人发出同情),第一次认真参加比赛,真正比赛的时候感觉没有那么正式,很乱,各种小问题,(例如博主就没找到题目在哪里,找到后又不 ...
- 第八届蓝桥杯java b组第六题
标题:最大公共子串 最大公共子串长度问题就是:求两个串的所有子串中能够匹配上的最大长度是多少. 比如:"abcdkkk" 和 "baabcdadabc",可以找 ...
- [18/12/3]蓝桥杯 练习系统 入门级别 Fibonacci数列求模问题 题解思路
前言略. 看到这个题目本来应该很高兴的,因为什么,因为太TM的基础了啊! 可是当你用常规方法尝试提交OJ时你会发现..hhh...运行超时..(开心地摇起了呆毛 //Fibonacci数列递归一般问题 ...
- 第六届蓝桥杯C++B组省赛
1.奖券数目 2.星系炸弹 3.三羊献瑞 4.格子中输出 5.九数组分数 6.加法变乘法 7.牌型种数 8.移动距离 9.垒骰子 10.生命之树 1.奖券数目 奖券数目有些人很迷信数字,比如带“4”的 ...
- 第三届蓝桥杯C++B组国(决)赛真题
解题代码部分来自网友,如果有不对的地方,欢迎各位大佬评论 题目1.星期几 1949年的国庆节(10月1日)是星期六. 今年(2012)的国庆节是星期一. 那么,从建国到现在,有几次国庆节正好是星期日呢 ...
- 第七届蓝桥杯C++B组省赛
1.煤球数目 2.生日蜡烛 3.凑算式 4.快速排序 5.抽签 6.方格填数 7.剪邮票 8.四平方和 9.交换瓶子 10.最大比例 今天是周三了,周天刚考完,这次做的还是不好(上次是全省最后一名). ...
- 2012年第三届蓝桥杯Java本科组省赛试题解析
题目地址:https://wenku.baidu.com/view/326f7b4be518964bcf847c96.html?rec_flag=default => 百度文档 题目及解析 ...
随机推荐
- 使用macaca抓页面元素，执行命令后报安装失败处理Error: Command failed: ……pm install -r "/data/local/tmp/com.macaca.android.testing"
最近换了小米手机做自动化测试,执行命令的时候报安装失败错误,错误如下 解决:设置小米允许USB安装就好了 pm install -r "/data/local/tmp/com.macaca. ...
- 09_EM算法
今天是2020年3月5日星期四.预计开学时间不会早于四月初,真是好消息,可以有大把的时间整理知识点(实际上发文章的时间都6月6号了,希望9月份能开学啊,不耽误找工作~).每次导师找,整个人会变的特别烦 ...
- iOS－字典转模型（单模型）的实现
用模型取代字典的好处 使用字典的坏处 一般情况下,设置数据和取出数据都使用“字符串类型的key”,编写这些key时,编译器不会有任何友善提示,需要手敲, eg:dict[@"name&quo ...
- MySQL查询优化利刃-EXPLAIN
有一个 ? 遇到这样一个疑问:当where中In一个索引字段,那么在查询中还会使用到索引吗? SELECT * FROM table_name WHERE column_index in (expr) ...
- 制作zipkin docker镜像
这里使用的zipkin知识基于内存的版本,没有接入外部存储 https://zipkin.io/ https://github.com/openzipkin/zipkin https://github ...
- jetty 启动项目在pom.xml 的配置
<build> <finalName>${artifactId}</finalName> <resources> <resource> &l ...
- JVM内存结构详解
从java编程语言说起... 1. Java编程语言简介 1.1 编程语言概述 系统级和应用级 系统级:C,C++,go,erlang 应用级:C#,Java,Python,Perl,Ruby,php ...
- Redis的持久化设计
Redis 持久化设计 持久化的功能:Redis是内存数据库,数据都是存储在内存中的,为了避免进程退出导致数据的永久丢失,要定期将Redis中的数据以某种形式从内存保存到硬盘,当下次Reids重启时, ...
- 附015.Kubernetes其他技巧
一 优化镜像源 1.1 国内镜像源 global proxy in China format example dockerhub (docker.io) dockerhub.azk8s.cn dock ...
- Laravel模板引擎Blade中section的一些标签的区别介绍
Laravel 框架中的 Blade 模板引擎,很好用,但是在官方文档中有关 Blade 的介绍并不详细,有些东西没有写出来,而有些则是没有说清楚.比如,使用中可能会遇到这样的问题: 1.@yield ...