奇怪DP之步步为零

题目

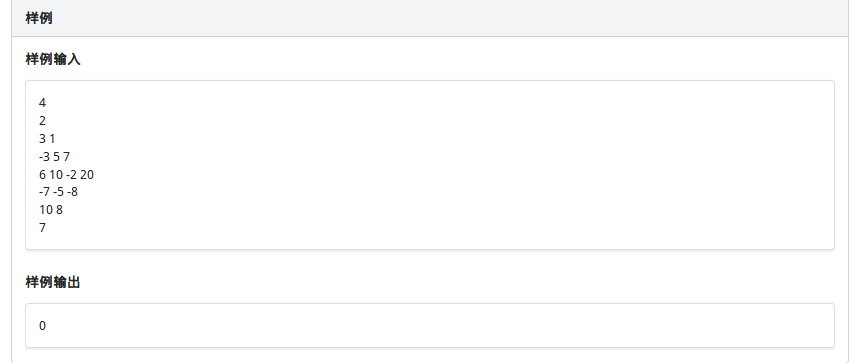
思路

很明显的dp就是不会跑啊，所以最后dfs救了一下场，不出所料，最后果然T了，现在说一下正解。

• 为什么说是奇怪dp呢，这道题的dp数组是布尔型的，f[i][j][k]代表在到第i行第j列之前是否能组成k，1（能）或者0（不能）;
• 这道题还有一个恶心的地方，就是原始数的存放，可以分n以及n前和n后两个部分来存
• 为了f数组的第三维不为负数（RE欢迎你），我们进行以下操作

• 将存入的数都换为正数，因为对于每一位都有加减两种操作
• 对于每一行，维护一个最大值Max，求\(tot=\sum_{i=1}^{2*n-1} Max_i\)，然后在第三维的基础值为tot（统一上移tot位）

• 然后就是dp了

for(int i=2*n-1;i>n;i--){
		for(int j=1;j<=2*n-i;j++){
			for(int k=0;k<=2*tot;k++){
				if(dp[i][j][k]){
					now=k+a[i][j];
					if(judge(now))dp[i-1][j][now]=dp[i-1][j+1][now]=1;
					now=k-a[i][j];
					if(judge(now))dp[i-1][j][now]=dp[i-1][j+1][now]=1;
				}
			}
		}
	}
	for(int i=n;i>=1;i--){
		for(int j=1;j<=i;j++){
			for(int k=0;k<=2*tot;k++){
				if(dp[i][j][k]){
					now=k+a[i][j];
					dp[i-1][j][now]=dp[i-1][j-1][now]=1;
					now=k-a[i][j];
					dp[i-1][j][now]=dp[i-1][j-1][now]=1;
				}
			}
		}
	}

分两部分，注意f存的是i行j列>>前<<能否组成k的情况！！如果可以，则就对当前状态进行转移，加或者减

代码

#include<bits/stdc++.h>
using namespace std;
int a[100][60];
int dp[100][60][6005];
int n,tot,Max;
bool judge(int x){
    if(x<0 || x>2*tot)return 0;
    return 1;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		int Max=0;
		for(int j=1;j<=i;j++){
			scanf("%d",&a[i][j]);
			a[i][j]=abs(a[i][j]);
			Max=max(a[i][j],Max);
		}
		tot+=Max;
	}
	for(int i=1;i<n;i++){
		int Max=0;
		for(int j=1;j<=n-i;j++){
			scanf("%d",&a[n+i][j]);
			a[n+i][j]=abs(a[n+i][j]);
			Max=max(a[n+i][j],Max);
		}
		tot+=Max;
	}
	dp[2*n-1][1][tot]=1;
	int now=0;
	for(int i=2*n-1;i>n;i--){
		for(int j=1;j<=2*n-i;j++){
			for(int k=0;k<=2*tot;k++){
				if(dp[i][j][k]){
					now=k+a[i][j];
					if(judge(now))dp[i-1][j][now]=dp[i-1][j+1][now]=1;
					now=k-a[i][j];
					if(judge(now))dp[i-1][j][now]=dp[i-1][j+1][now]=1;
				}
			}
		}
	}
	for(int i=n;i>=1;i--){
		for(int j=1;j<=i;j++){
			for(int k=0;k<=2*tot;k++){
				if(dp[i][j][k]){
					now=k+a[i][j];
					dp[i-1][j][now]=dp[i-1][j-1][now]=1;
					now=k-a[i][j];
					dp[i-1][j][now]=dp[i-1][j-1][now]=1;
				}
			}
		}
	}
	int ans=0x7f7f7f7f;
	for(int i=0;i<=2*tot;i++){
		if(dp[0][0][i]){
			ans=min(ans,abs(i-tot));
		}
		if(dp[0][1][i]){
			ans=min(ans,abs(i-tot));
		}
	}
	printf("%d\n",ans);
}