WPF3D立方体图形展开动画思路

WPF3D立方体图形展开动画

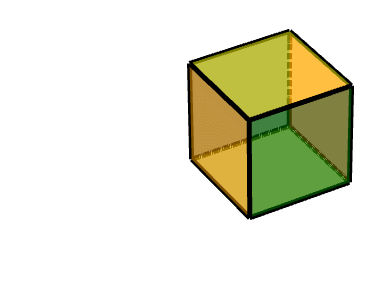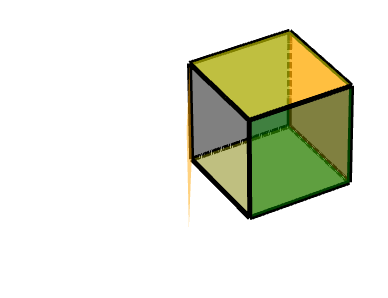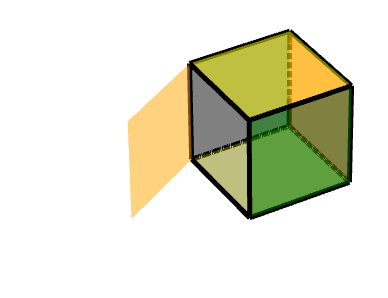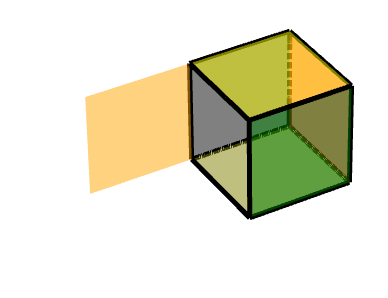
效果图:

规定：

立方体中心为（000），棱长为2，则（111）（-1-1-1）等1，-1三维组合的八个点为其顶点

坐标系：

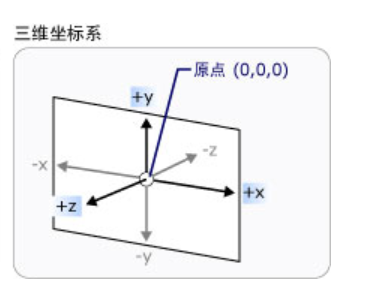
补充：

WPF 3D 分为中心对称旋转（RotateTransform3D），平移旋转（TranslateTransform3D）和比例缩减（ScaleTransform3D），立体图形展开目前只用到对称和平移变换

1 按轴旋转的面

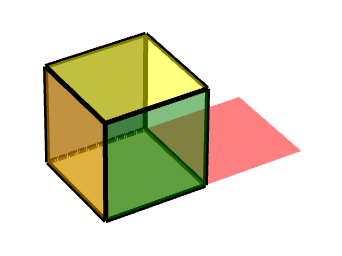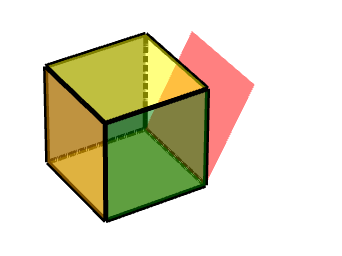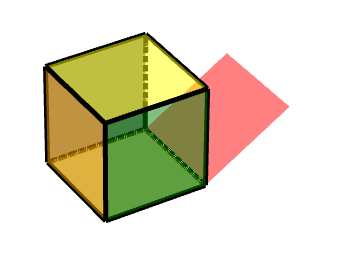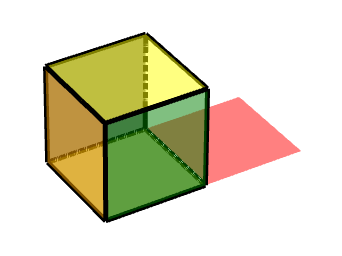
如图所示，则其是按照由（-1-1-1）到（1-1-1）的轴运动

换算成中心对称，也就是这条边的中点，则对称点为（0，-1，-1）

此动画可描述为，对点（0，-1，-1）做中心对称变换，沿X轴旋转90度。

Code:

			//设置对称中心
	    face0RotateTransform3D.CenterX = 0;
            face0RotateTransform3D.CenterY = -1;
            face0RotateTransform3D.CenterZ = -1;
			//设置旋转角度
            (face0RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(1, 0, 0);
            DoubleAnimation face0AxisAngleRotation3DAnimation = new DoubleAnimation();
            face0AxisAngleRotation3DAnimation.From = 0;
            face0AxisAngleRotation3DAnimation.To = -90;
            face0AxisAngleRotation3DAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));

同理可得另一个面：对点（1，-1，-1）做中心对称变换，沿Z轴旋转90度。

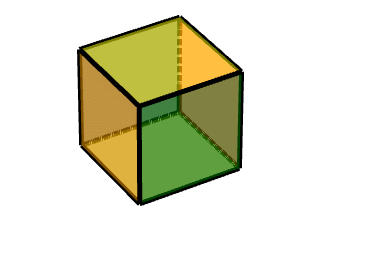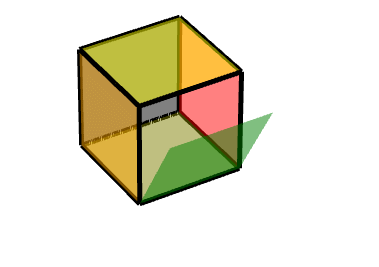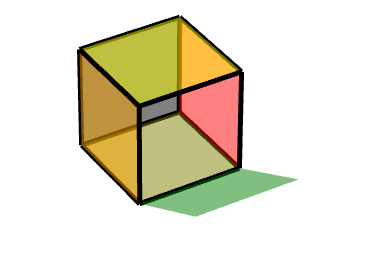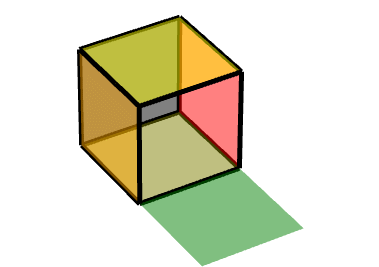
Code：

 	    face3RotateTransform3D.CenterX = 1;
            face3RotateTransform3D.CenterY = -1;
            face3RotateTransform3D.CenterZ = -1;
            (face3RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 0, 1);
            DoubleAnimation DoubleAnimation = new DoubleAnimation();
            DoubleAnimation.From = 0;
            DoubleAnimation.To = -90;

2 连接按轴旋转的面的面

即二级旋转面

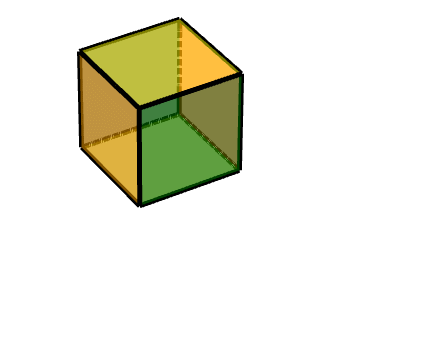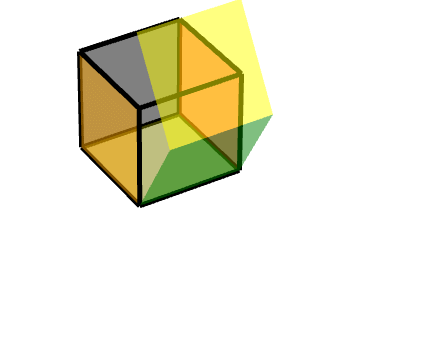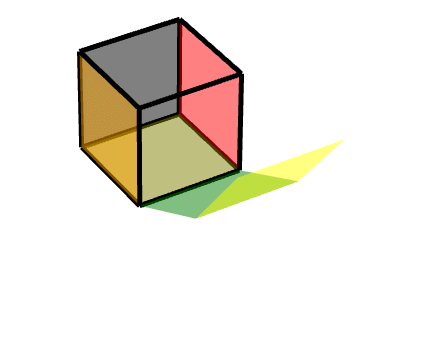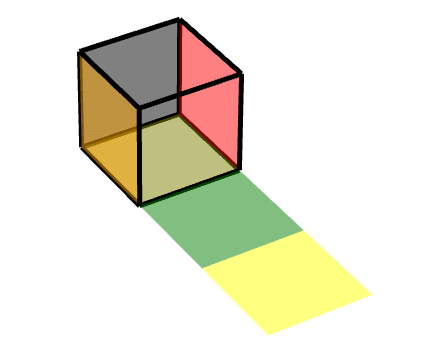
此时，我们可以把它理解为两个旋转的结合，一个轴对称旋转+一个平移旋转

1 轴对称旋转：

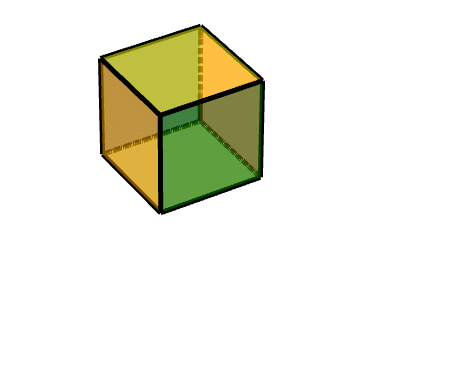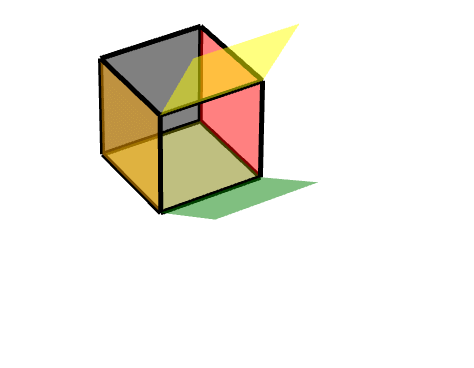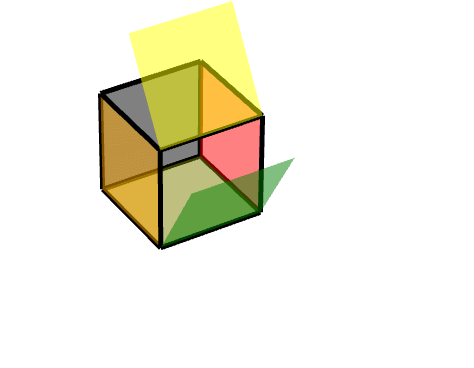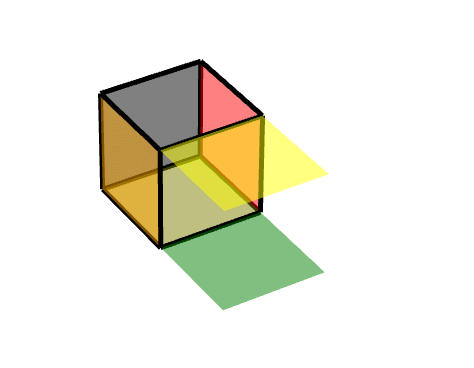
描述为，对点(11-1)进行旋转，沿Z轴旋转180度。

Code：

            face4RotateTransform3D.CenterX = 1;
            face4RotateTransform3D.CenterY = 1;
            face4RotateTransform3D.CenterZ = -1;
            (face4RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 0, 1);
            DoubleAnimation DoubleAnimation = new DoubleAnimation();
            DoubleAnimation.From = 0;
            DoubleAnimation.To = -180;

2 平移旋转：

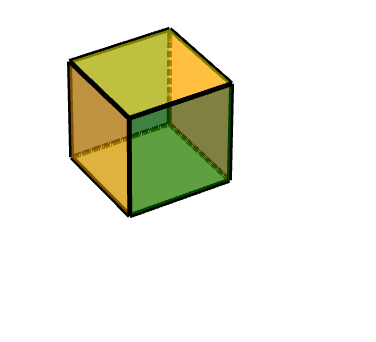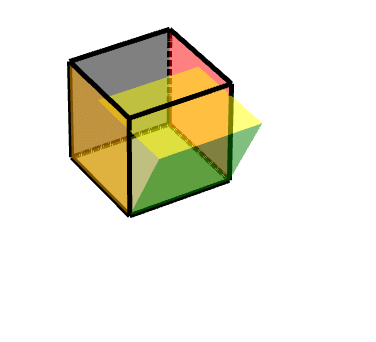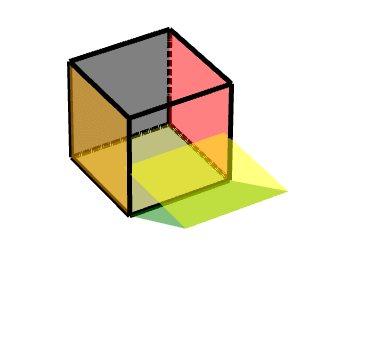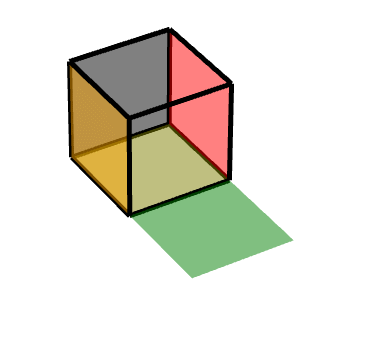
从侧面看的平移轨迹：

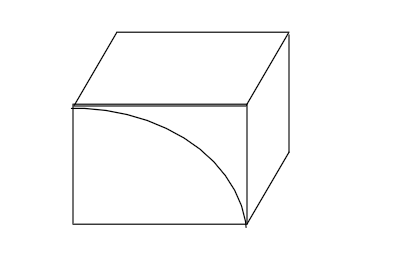
此平移按X和Y轴方向分解示意图：

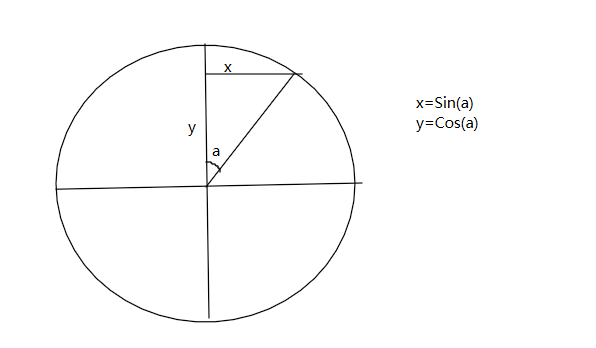
其中X方向可以描述为：

在t时间内，L为边长

x方向值为：x=L*Sin(a)

y方向值为：y=L*Cos(a)

其中角度a可描述为：(PI/2)*currentTime/totalAnimationDuration

如果我们将动画描述成帧动画，综上：

X方向平移动画帧

 LinearDoubleKeyFrame GetFace4OffsetXKeyFrame(double time)
        {
            return new LinearDoubleKeyFrame(borderLength * Math.Sin(time * (Math.PI / 2) / keyFrameAnimationTotalTimeM), KeyTime.FromTimeSpan(TimeSpan.FromSeconds(time)));
        }

Y方向平移动画帧

  LinearDoubleKeyFrame GetFace4OffsetYKeyFrame(double time)
        {
            return new LinearDoubleKeyFrame(-(borderLength - borderLength * Math.Cos(time * (Math.PI / 2) / keyFrameAnimationTotalTimeM)), KeyTime.FromTimeSpan(TimeSpan.FromSeconds(time)));
        }

3 三级旋转面

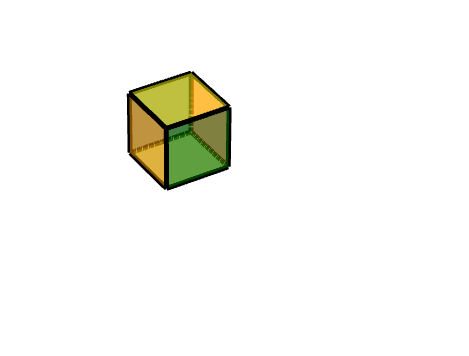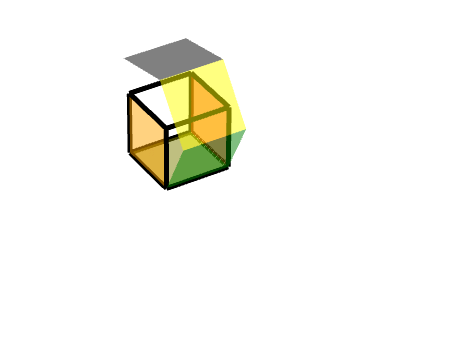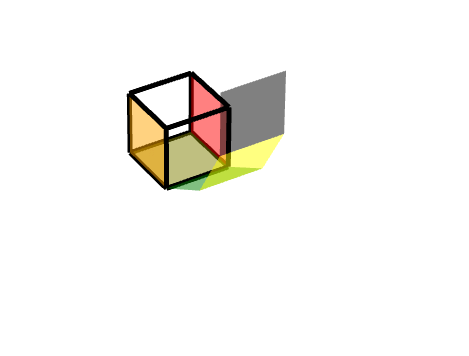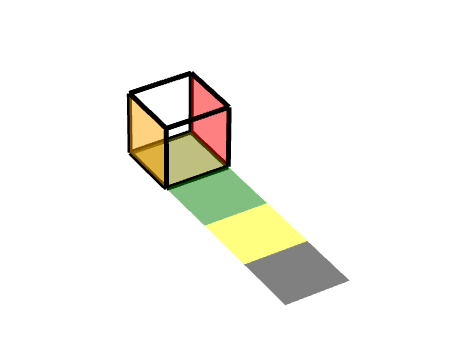
同理，我们可以把它理解为两个旋转的结合，一个轴对称旋转+一个平移旋转

轴对称旋转：

描述为，对点(-110)进行旋转，沿Z轴旋转270度。

Code：

            face1RotateTransform3D.CenterX = -1;
            face1RotateTransform3D.CenterY = 1;
            face1RotateTransform3D.CenterZ = 0;
            (face1RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 0, 1);
            DoubleAnimation DoubleAnimation = new DoubleAnimation();
            DoubleAnimation.From = 0;
            DoubleAnimation.To = -270;
            DoubleAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));

平移旋转：

平移旋转的量需要通过分解轴旋转来得出。

通过观察我们可以将其分为两个轴旋转，第一个旋转是该面沿着A轴的轴对称旋转（自身旋转），第二个是二级面的沿着B轴的轴对称旋转（相对面旋转）

A棱边沿着A·轨迹旋转，B棱边沿着B·轨迹旋转

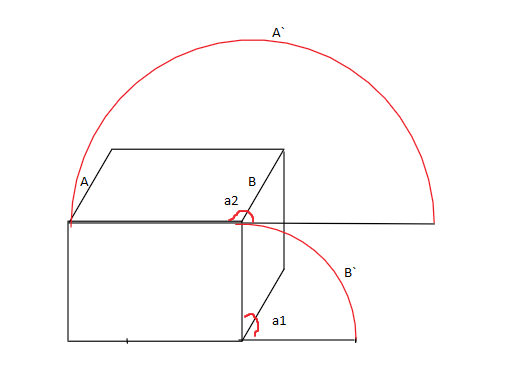
则沿着B轴的旋转，与二级面分解一样：

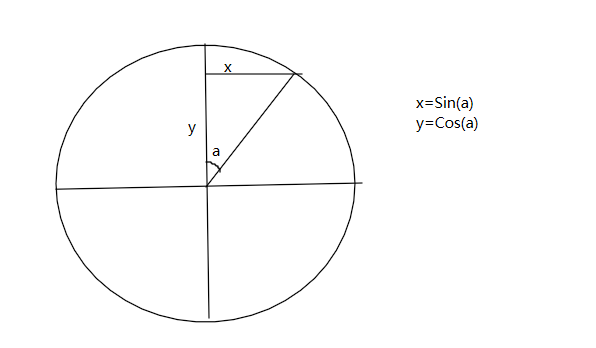
A轴旋转分解:

对于y，y=Sin(a2)

对于x，分为两种情况：

当a2处于0-PI/2时，x=Cos(a2)，

当a2处于PI/2-PI时，y=L-Cos(a2)

把上述两个分解加一起就得到了X=xa+xb，y=ya+yb，

Code：

X

 LinearDoubleKeyFrame GetFace1OffsetXKeyFrame(double time)
        {
            //自身边的定位坐标
            double angle = time / keyFrameAnimationTotalTimeM;
            double xa, xb;
            double xTotal;
            if (angle <= 1 / 2)
            {
                //0-1/2PI
                xa = borderLength * Math.Cos(Math.PI * time / keyFrameAnimationTotalTimeM);
            }
            else
            {
                //1/2PI-PI
                xa = borderLength - borderLength * Math.Cos(Math.PI * time / keyFrameAnimationTotalTimeM);
            }
            //前轴定位坐标
            xb = borderLength * Math.Sin((Math.PI / 2) * time / keyFrameAnimationTotalTimeM);
            xTotal = xa + xb;
            return new LinearDoubleKeyFrame(xTotal, KeyTime.FromTimeSpan(TimeSpan.FromSeconds(time)));
        }

Y

 Timeline Face1ExpandedAnimation_MoveOffsetY_UsingKeyFrames()
        {
            DoubleAnimationUsingKeyFrames DoubleAnimation = new DoubleAnimationUsingKeyFrames();
            DoubleAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));
            DoubleAnimation.Completed += ((sender, e) =>
            {
                faceStoryboard.Remove(tileButton);
            });
            Storyboard.SetTargetName(DoubleAnimation, "face1TranslateTransform3D");
            Storyboard.SetTargetProperty(DoubleAnimation,
                new PropertyPath(TranslateTransform3D.OffsetYProperty));

            for (double i = 0; i <= keyFrameAnimationTotalTimeM + keyFrameAnimationIntervalM; i += keyFrameAnimationIntervalM)
            {
                DoubleAnimation.KeyFrames.Add(GetFace1OffsetYKeyFrame(i));
            }
            return DoubleAnimation;
        }C

4 双重轴对称旋转+平移旋转面

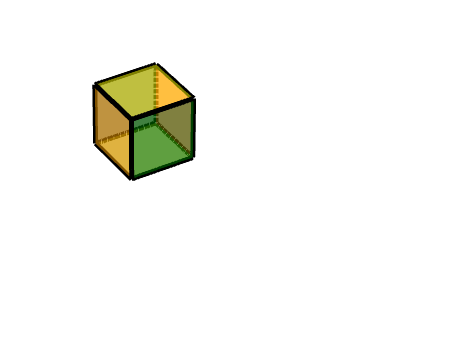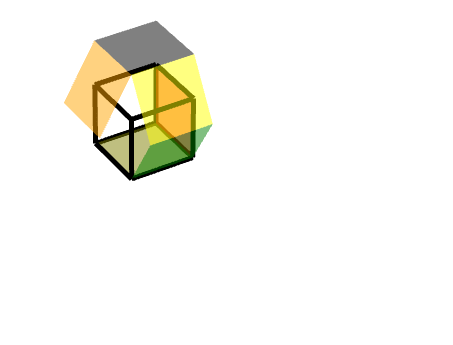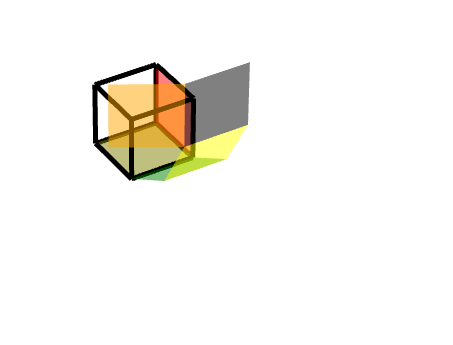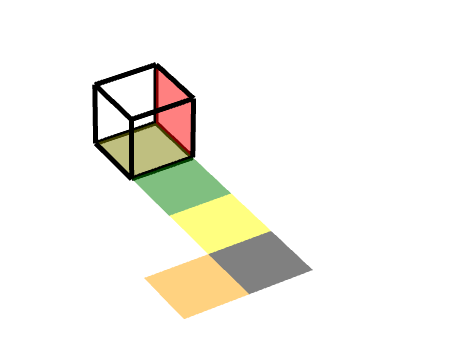
如图所示，左边这个橙色的面，在黑色的三级旋转面之上又增加一个沿着Z轴的旋转。

此时可以简单地分解为三级旋转面的旋转+沿着Z轴的旋转。

三级旋转面的旋转：

见上文

Z轴旋转

可描述为：对点(-1-11)进行旋转，沿Z轴旋转90度。

            face5RotateTransform3D.CenterX = -1;
            face5RotateTransform3D.CenterY = -1;
            face5RotateTransform3D.CenterZ = 1;
            (face5RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 1, 0);
            DoubleAnimation DoubleAnimation = new DoubleAnimation();
            DoubleAnimation.From = 0;
            DoubleAnimation.To = -90;
            DoubleAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));