T2695 桶哥的问题——送桶 题解

校内测试 ------T2

看完这个题，就觉得和贪心那一块的任务调度很像，于是思路就是贪心啦！

蒟蒻的我，也就只能想到用贪心了，但是不知道怎么用qwq

这是我考试当时的思路，数据水骗了80分qwq：

模拟了样例以后，发现了答案好像就是结束时间最大的那个再减去所有任务的时间（现在觉得有点不现实，数据是真的水）；

又试了几组，发现如果有某个任务的结束时间和所用时间相同，那么答案一定为0，然后我又加了这个条件进去，然后就80分了。

下面说正解：

首先题目说明了“保证答案大于等于0”，也就是说明一定有解，那么就是每一个任务一定会被完成！

考虑对于任何一个任务i，我们都要尽量往后来安排它，最好还是卡着它的结束时间点，这样的话才是最优解

Why？-----减小对其他任务的影响！

看下面这个例子，如果我们不是将任务一贴着结束时间点放，而是任意放的话，那么可能就会影响到其他的任务！

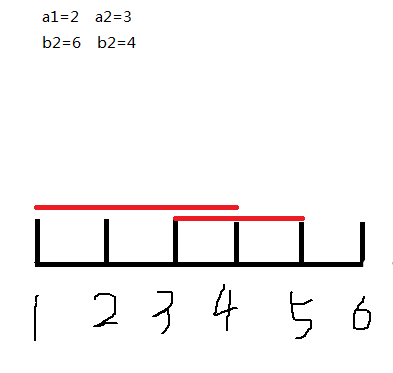
看下面的例子，这是一个所用时间为2，结束时间为6的任务，显然上面的解不是最优解，因为4到6的两个时间可以用来偷懒啊qwq，所以尽量贴着结束时间点；

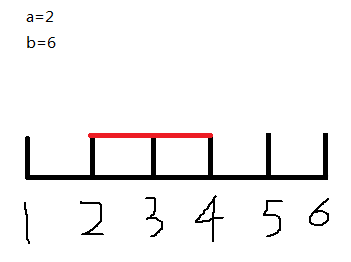
既然贴着结束时间点了，那么红色的那一部分我们就不用考虑了，因为做不了其他任务；

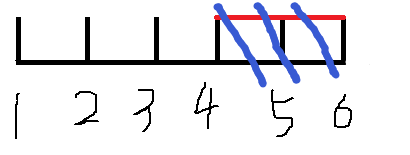
综合上面的几点，我们可以得到一个基本的做法了：

1.按照结束时间从大到小排序，让答案ans等于结束时间最大的那个；

2.ans减去该结束时间点所对应的任务所需的时间；

3.重点核心：若当前的ans值大于当前访问的结束时间点，让ans等于该结束时间点，再减去该任务所需的时间；

4.从结束时间大到小，重复第二步；

图解：

1.找到一个结束时间最大的任务---任务一（结束时间为6），此时ans=6；减去当前任务所需的时间，更新ans=6-2=4；

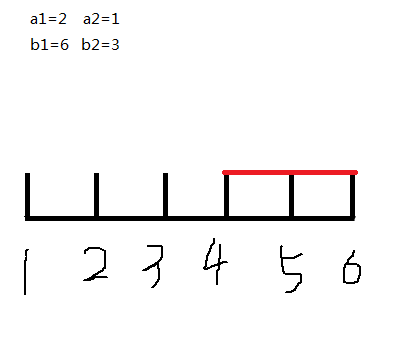
2.来到了第二个任务：发现该任务的结束时间点为3，比当前的ans要小！于是我们更新ans=b2=3，再减去当前任务的时间，更新ans=3-1=2；

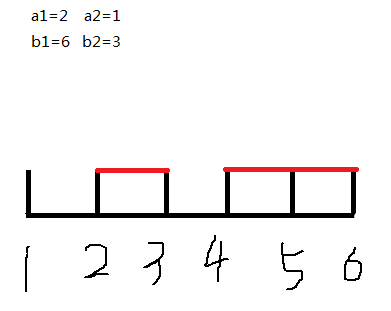
那么最后的答案就是2了！

多次模拟以后，我们就懂得其中的巧妙用意了：

还是上面的例子，如果第二步没有使ans=b2，那么我们就会这样放置第二个任务：

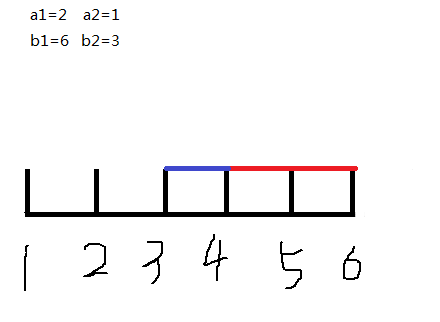
因为每一步都是贪心贴着结束时间点来放置的，所以这就使得结束点为3的任务在4的时候完成！这是不合法的！

所以我们还要每次看看当前ans值是否小于当前任务的结束时间点，来保证每一步都是合法的！

OK，理解到这里，代码就出来了，是那么的短：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int read()
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
    if(ch=='-') x=-x;
    ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=a*+(ch-'');
        ch=getchar();
    }
    return a*x;
}
int n;
struct tong
{
    int date,time;
}a[];
int cmp(tong x,tong y)
{
    return x.date>y.date;
}
int main()
{
    n=read();
    for(int i=;i<=n;i++)
    {
        a[i].time=read();
        a[i].date=read();
    }
    sort(a+,a++n,cmp);
    long long ans=a[].date;
    for(int i=;i<=n;i++)
    {
        if(ans>a[i].date) ans=a[i].date;
        ans-=a[i].time;
    }
    cout<<ans;
    return ;
}

对了，昨天没写完博客是因为8：25去看推荐生成绩了qwq（紧张 ，还好推荐生过了！！！

撒花祝贺qwq～～～