数据结构与算法（周测2-AVL树）
判断题
1.The inorder traversal sequence of an AVL tree must be in sorted (non-decreasing) order.
T
F
根据二叉搜索树性质，中序遍历一定是有序的，而且是递增的。
2.Insert 1, 2, 3, 4, 5, and 6 one by one into an initially empty AVL tree. Then the preorder traversal sequence of the resulting tree must be {4, 2, 1, 3, 5, 6}.
T
F
最终的AVL树：
3.For any node in an AVL tree, the height of the left subtree must be greater than that of the right subtree.
T
F
4.For an AVL tree, the balance factors of all the non-leaf nodes are 0 iff the tree is a complete binary tree.
T
F
只有完美二叉树满足这个定义。
5.If the depth of an AVL tree with nodes { 1, 2, 3, 4 } is 3 (the depth of the root is 1), then either node 2 or node 3 must have two children.
T
F
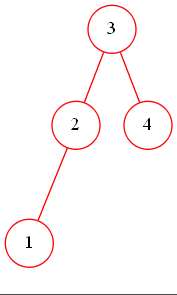
6.任何AVL树的中序遍历结果是有序的（从小到大）。
T
F
7.将1、2、3、4、5、6顺序插入初始为空的AVL树中，当完成这6个元素的插入后，该AVL树的先序遍历结果是：4、2、1、3、5、6。
T
F
见第二题。
8.For any node in an AVL tree, the height of the right subtree must be greater than that of the left subtree.
T
F
9.对AVL树中的任一结点，其左子树的高度一定比其右子树的高度要高。
T
F
10.An AVL tree with the balance factors of all the non-leaf nodes being 0 must be a perfect binary tree.
T
F
所有的非叶结点的平衡因子都是0，意味着左右子树的高度都相同，只有当树是完美二叉树的时候才满足。
11.对一棵平衡二叉树，所有非叶结点的平衡因子都是0，当且仅当该树是完全二叉树。
T
F
应该是完美二叉树，完全二叉树最后一层结点不一定要满，这样父结点中肯定会有平衡因子不为0的结点。
12.若一棵平衡二叉树的所有非叶结点的平衡因子都是0，则其必为完美二叉树。
T
F
同第10题
13.If the depth of an AVL tree with nodes { 1, 2, 3, 4 } is 3 (the depth of the root is 1), then it is possible for node 4 to be the root.
T
F
如果4是根结点，右子树上肯定没有元素，即使左子树上深度只能为1，而结点有3个，不可能。
14.如果由结点{ 1, 2, 3, 4 }组成的AVL树的深度是3（根结点的深度是1），则结点2或者结点3一定有两个子结点。
T
F
同第5题。
15.如果由结点{ 1, 2, 3, 4 }组成的AVL树的深度是3（根结点的深度是1），则结点4有可能是根结点。
T
F
同第13题。
选择题
1.Which of the following is TRUE for any node in an AVL tree?
B.The absolute value of the difference between the heights of left and right subtrees is no more than 1
C.The height of the left subtree is always greater than that of the right subtree
D.The height of the left subtree is always less than that of the right subtree
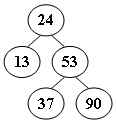
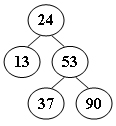
2.Insert key 48 into the balanced binary tree shown by the figure. Then in the resulting balanced tree, the left- and right-child of key 37 are:
B.24 and 48
C.24 and 53
D.24 and 90
插入后的树：
3.Insert 2, 1, 4, 5, 9, 3, 6, 7 into an initially empty AVL tree. Which one of the following statements is FALSE?
B.3 and 7 are siblings
C.2 and 6 are siblings
D.9 is the parent of 7
插入后的树：
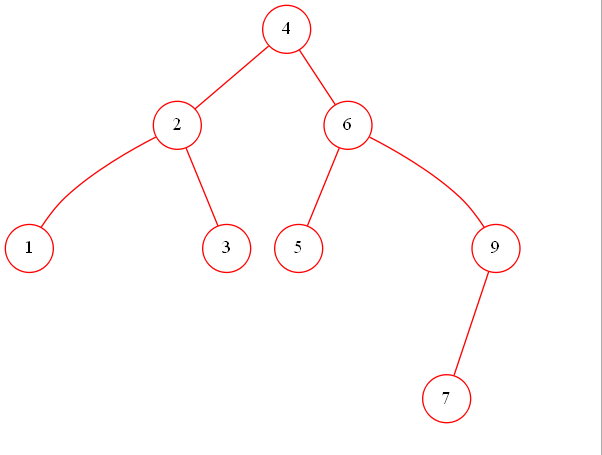
4.If the depth of an AVL tree is 5 (the depth of an empty tree is defined to be ?1), then the minimum possible number of nodes in this tree is:
B.20
C.33
D.64
根据递推公式F(N)=F(N-1)+F(N-2)+1，得到序列F(1)=1,F(2)=2,F(3)=4,F(4)=7,F(5)=12,F(6)=20。
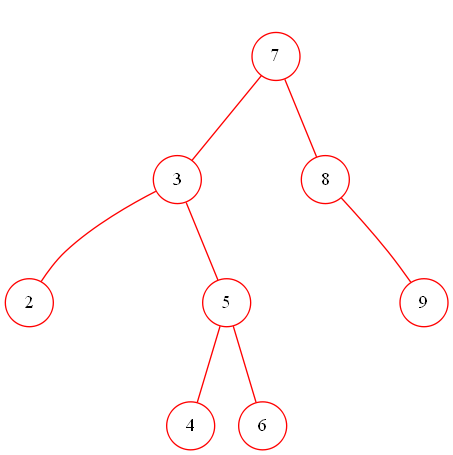
5.Insert { 9, 8, 7, 2, 3, 5, 6, 4} into an initially empty AVL tree. Which one of the following statements is FALSE?
B.2 and 5 are siblings
C.there are 2 nodes with their balance factors being -1
D.the height of the resulting AVL tree is 3
插入后的树：
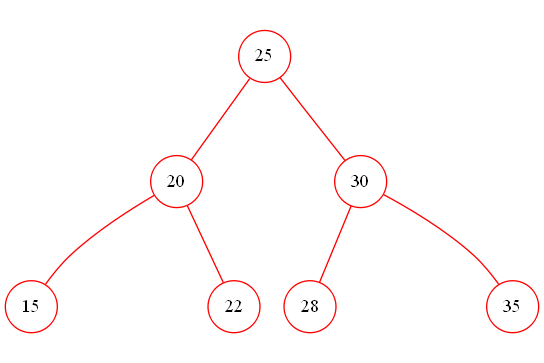
6.After inserting 28, 22, and 35 into the given AVL tree, the children of node 25 are __。
B.20 and 28
C.22 and 30
D.20 and 30
插入后的树：
7.下列二叉搜索树中，满足平衡二叉树定义的是：
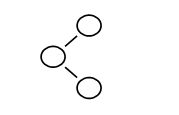
B.
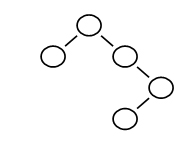
C.
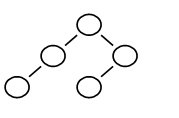
D.
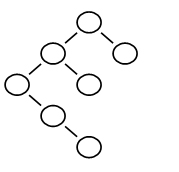
其他几个平衡因子太大了
8.在下列所示的平衡二叉树中，插入关键字48后得到一棵新平衡二叉树。在新平衡二叉树中，关键字37所在结点的左、右子结点中保存的关键字分别是：
B.24、48
C.24、53
D.24、90
同第2题
9.12个结点的AVL树的最大深度是？
B.4
C.5
D.6
类似第4题，但与第4题不同的是，一般认为空树深度是0，所以选5。
10.若AVL树的深度是6（空树的深度定义为-1），则该树的最少结点数是：
B.17
C.20
D.33
类似第4题。
11.Among the following trees, which one satisfies the definition of a balanced tree?
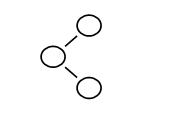
B.
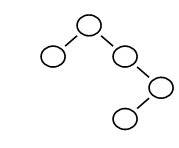
C.
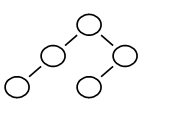
D.
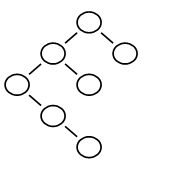
同第7题
12.The maximum possible depth of an AVL tree with 12 nodes is:
B.4
C.5
D.6
同第9题
13.Insert {88, 70, 61, 96, 120, 90} one by one into an initially empty AVL tree. Then the preorder traversal sequence of the resulting AVL tree is:
B.90,70,61,88,96,120
C.88,70,61,90,96,120
D.88,70,61,96,90,120
插入后的树：
14.If the depth of an AVL tree is 6 (the depth of an empty tree is defined to be -1), then the minimum possible number of nodes in this tree is:
B.17
C.20
D.33
同第14题
15.将 2, 1, 4, 5, 9, 3, 6, 7 顺序插入一棵初始为空的AVL树。下列句子中哪句是错的？
B.3 和 7 是兄弟
C.2 和 6 是兄弟
D.9 是 7 的父结点
同第3题
16.如果AVL树的深度为5（空树的深度定义为-1），则此树最少有多少个结点？
B.20
C.33
D.64
同第4题
17.如果AVL树的深度为6（空树的深度定义为-1），则此树最少有多少个结点？
B.20
C.33
D.64
类似第4题
18.将一系列数字顺序一个个插入一棵初始为空的AVL树。下面哪个系列的第一次旋转是"右-左"双旋？
B.6,5,4,3,2,1
C.4,2,5,6,3,1
D.3,1,4,6,5,2
A、B选项都是单旋转，C选项不用旋转
19.将 1, 2, 3, 6, 5, 4 顺序一个个插入一棵初始为空的AVL树，会经历下列哪些旋转？
B.一个"右-右"旋、一个"右-左"旋、一个"左-右"旋
C.一个"右-右"旋和两个"右-左"旋
D.两个"右-右"旋和一个"左-右"旋
当插入3的时候，结点全在右子树上，执行一次"右-右"旋；当插入5的时候，3、6、5需要执行一次"右-左"旋；当插入4时，2，5，6需要执行一次"右-左"旋
20.在任意一棵非空平衡二叉树（AVL 树）T1 中，删除某结点 v 之后形成平衡二叉树 T2，再将 v 插入 T2 形成平衡二叉树 T3。下列关于 T1 与 T3 的叙述中，正确的是：
- I、若 v 是 T1 的叶结点，则 T1 与 T3 可能不相同
- II、若 v 不是 T1 的叶结点，则 T1 与 T3 一定不同
- III、若 v 不是 T1 的叶结点，则 T1 与 T3 一定相同
B.仅 II
C.仅 I、II
D.仅 I、III
数据结构与算法（周测2-AVL树）的更多相关文章
- Java数据结构和算法（七）B+ 树
Java数据结构和算法(七)B+ 树 数据结构与算法目录(https://www.cnblogs.com/binarylei/p/10115867.html) 我们都知道二叉查找树的查找的时间复杂度是 ...
- 为什么我要放弃javaScript数据结构与算法（第八章）—— 树
之前介绍了一些顺序数据结构,介绍的第一个非顺序数据结构是散列表.本章才会学习另一种非顺序数据结构--树,它对于存储需要快速寻找的数据非常有用. 本章内容 树的相关术语 创建树数据结构 树的遍历 添加和 ...
- 看图轻松理解数据结构与算法系列(NoSQL存储-LSM树) - 全文
<看图轻松理解数据结构和算法>,主要使用图片来描述常见的数据结构和算法,轻松阅读并理解掌握.本系列包括各种堆.各种队列.各种列表.各种树.各种图.各种排序等等几十篇的样子. 关于LSM树 ...
- Android版数据结构与算法(七):赫夫曼树
版权声明:本文出自汪磊的博客,未经作者允许禁止转载. 近期忙着新版本的开发,此外正在回顾C语言,大部分时间没放在数据结构与算法的整理上,所以更新有点慢了,不过既然写了就肯定尽力将这部分完全整理好分享出 ...
- 数据结构系列（2）之 AVL 树
本文将主要讲解平衡二叉树中的 AVL 树,其中将重点讲解二叉树的重平衡方法,即左旋和右旋,以及 3+4 重构:这些方法都是后面要讲的 B 树,红黑树等 BBST 的重要基础:此外在看本文之前最好先看一 ...
- 17-看图理解数据结构与算法系列(NoSQL存储-LSM树)
关于LSM树 LSM树,即日志结构合并树(Log-Structured Merge-Tree).其实它并不属于一个具体的数据结构,它更多是一种数据结构的设计思想.大多NoSQL数据库核心思想都是基于L ...
- 【数据结构与算法】Trie（前缀树）模板和例题
Trie 树的模板 Trie 树的简介 Trie树,又称字典树,单词查找树或者前缀树,是一种用于快速检索的多叉树结构,如英文字母的字典树是一个26叉树,数字的字典树是一个10叉树.他的核心思想是空间换 ...
- [数据结构与算法]哈夫曼(Huffman)树与哈夫曼编码
声明:原创作品,转载时请注明文章来自SAP师太技术博客( 博/客/园www.cnblogs.com):www.cnblogs.com/jiangzhengjun,并以超链接形式标明文章原始出处,否则将 ...
- 10: java数据结构和算法: 构建哈夫曼树, 获取哈夫曼编码, 使用哈夫曼编码原理对文件压缩和解压
最终结果哈夫曼树,如图所示: 直接上代码: public class HuffmanCode { public static void main(String[] args) { //获取哈夫曼树并显 ...
- AVL树(三)之 Java的实现
概要 前面分别介绍了AVL树"C语言版本"和"C++版本",本章介绍AVL树的Java实现版本,它的算法与C语言和C++版本一样.内容包括:1. AVL树的介绍 ...
随机推荐
- PAT 甲级 1040 Longest Symmetric String (25 分)（字符串最长对称字串,遍历）
1040 Longest Symmetric String (25 分) Given a string, you are supposed to output the length of the ...
- Node.js ORM框架Sequelize使用示例
示例代码: const Sequelize = require('sequelize'); const sequelize = new Sequelize('database', 'username' ...
- [CareerCup] 2. Bomberman 炸弹人
We have a 2D grid. Each cell is either a wall, an enemy or empty. For example (0-empty, X-enemy, Y-w ...
- ELK之elasticsearch删除索引
参考文档:https://www.cnblogs.com/Dev0ps/p/9493576.html elasticsearch使用时间久了会产生大量索引占用磁盘空间,可以删除索引来释放 查看当前所有 ...
- 第八章 拦截器机制——《跟我学Shiro》
转发地址:https://www.iteye.com/blog/jinnianshilongnian-2025656 博客分类: 跟我学Shiro 跟我学Shiro 目录贴:跟我学Shiro目录贴 ...
- linux下的进程通信之信号量semaphore
概念: IPC 信号量和内核信号量非常相似,是内核信号量的用户态版本. 优点:每个IPC信号量可以保护一个或者多个信号量值的集合,而不像内核信号量一样只有一个值,这意味着同一个IPC资源可以保护多个独 ...
- 遵循统一的机器学习框架理解高斯混合模型（GMM）
遵循统一的机器学习框架理解高斯混合模型(GMM) 一.前言 我的博客仅记录我的观点和思考过程.欢迎大家指出我思考的盲点,更希望大家能有自己的理解. 本文参考了网络上诸多资料,特别是B站UPshuhua ...
- Nuget下载 MySql.Data 连接MySql数据库
打开VS项目,右键项目选择 右上角搜索框中搜索 MySql.Data 然后可以选择安装,但是可能会出现这个提示 这是因为版本的问题,所以,自己去官网重新下载,我这里选择的是这个版本, 官网地址: ht ...
- 基于Jquery ui 可复用的酒店 web页面选择入住日期插件
效果图: 代码: <!DOCTYPE html> <html> <head> <meta http-equiv="Content-Type" ...
- python 内置函数input/eval（22）
python的内置函数其实挺多的,其中input和eval算得上比较特殊,input属于交互式内置函数,eval函数能直接执行字符串表达式并返回表达式的值. 一.input函数 input是Pytho ...