JavaScript生成有序GUID或者UUID，这时就想到了雪花算法。

原理介绍：

snowFlake算法最终生成ID的结果为一个64bit大小的整数，结构如下图：

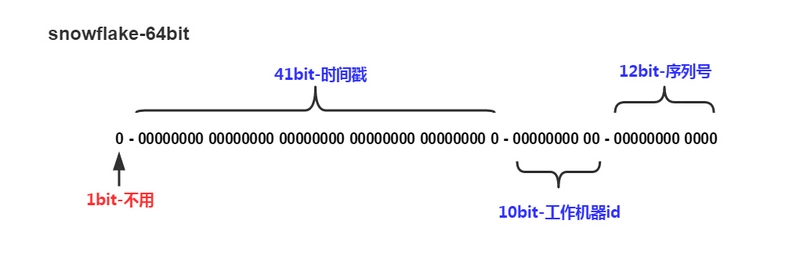
解释：

  • 1bit。二进制中最高位为1表示负数，但是我们最终生成的ID一般都是整数，所以这个最高位固定为0。
  • 41bit。用于记录时间戳（毫秒）
    • 41bit可以表示241-1个数字
    • 如果只用来表示正整数（计算机中正数包含0），可以表示的数值范围是0到241-1，减1是因为可表示的数值范围从0开始计算，而不是1.
    • 即41bit可以表示241-1个毫秒值转换为年为(241 - 1) / (1000 * 60 * 60 * 24 * 365) = 69.73年
  • 10bit。用于记录机器ID
    • 可以用于部署210=1024个节点，包含5bit 的 datacenterId 和5bit 的workerId
    • 5bit可以表示的最大正整数为25-1=31 即可以用0、1、2、3....31这32个数字来表示不同的datacenterId 和 workerId
  • 12bit。序列号用于记录相同毫秒内产生的不同ID
    • 12bit可以表示的最大正整数为212-1 = 4095，可以用0、1、2、3...4094这4095个数字来表示同一机器同一时间戳（毫秒）内产生的4095个ID序号

snowFlake算法可以保证：所有生成的ID按时间趋势递增；整个分布式系统内不会产生重复ID，由于5bit 的 datacenterId 和5bit 的workerId来区分。　

算法代码实现原理解释：

计算机中负数的二进制是用补码来表示的。

假设使用int类型来进行存储数字，int类型的大小是32bit二进制位，4个byte。(1byte = 8bit)

那么十进制中的3在二进制中的表示应该是：

00000000  00000000  00000000  00000011    // 3的二进制原码　　

那么数字 -3 在二进制中的表示应该是怎样的？试想： -3 + 3 = 0  在二进制运算中把 -3 的二进制看成未知数X来求解。

    00000000   00000000   00000000   00000011   // 3 原码

+   xxxxxxxx   xxxxxxxx   xxxxxxxx   xxxxxxxx   //  -3 补码

------------------------------------------------------

    00000000   00000000   00000000   00000000

反推X 即 二进制数从最低位开始逐位加1，使溢出的1不断向高位溢出，直到溢出到第33位，然后由于int类型最多只能保存32位二进制位，所以最高位的1溢出，剩余32位就成了0.

则：

    00000000   00000000   00000000   00000011   // 3 原码

+   11111111   11111111   11111111   11111101   //  -3 补码

---------------------------------------------------------

  1 00000000   00000000   00000000   00000000

总结公式：

  • 补码 = 反码 + 1
  • 补码 = (原码 - 1) 再取反码

workerIdBits = 5L;
maxWorkerId = -1L ^ (-1L << workerIdBits);

-1左移5位高位溢出的舍去后得到a，a与-1异或运算得到最终结果。

               11111111   11111111   11111111   11111111   // -1补码

       11111   11111111   11111111   11111111   11100000

---------------------------------------------------------------------

               11111111   11111111   11111111   11100000   //  高位溢出舍弃  
               11111111   11111111   11111111   11111111   // -1补码

    ^          11111111   11111111   11111111   11100000

---------------------------------------------------------------------

               00000000   00000000   00000000   00011111

24+23+22+21+20 = 16+8+4+2+1 = 31

-1L ^ (-1L << 5L) = 31 也就是 25-1 = 31， 该写法是利用位运算计算出5位能表示的最大正整数是多少。

用掩码mask防止溢出

seq = （seq  + 1) & seqMask

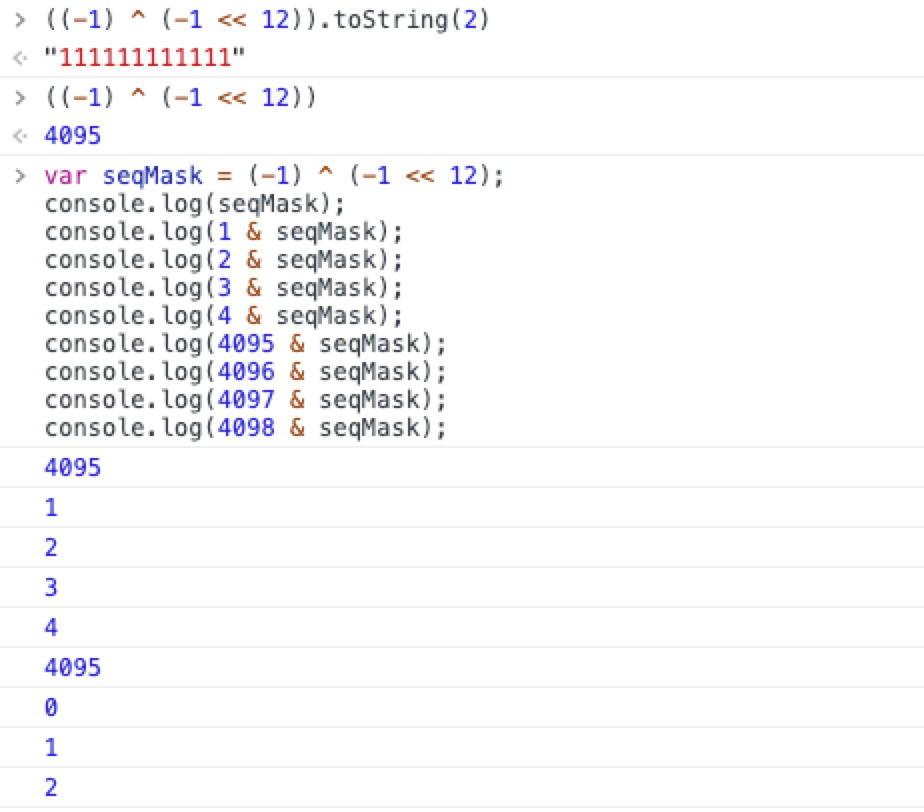
这段代码通过按位与运算保证计算的结果范围始终是0 - 4095.

按位运算结果：

return   ((timestamp - twepoch) << timestampLeftShift) |

            (datacnterId << datacenterIdShift) |

            (workerId << workerIdShift) |

            sequence;

解析：

var twepoch = 1571192786565; // 起始时间戳 用于当前时间戳减去这个时间戳得到偏移量

var workerIdBits = 5; // workId占用的位数5

var datacenterIdBit = 5;// datacenterId占用的位数5

var maxWorkerId = -1 ^ (-1 << workerIdBits); // workId可以使用的最大数值31

var maxDatacenterId = -1 ^ (-1 << datacenterIdBits); // datacenterId可以使用的最大数值31

var sequenceBit = 12;// 序列号占用的位数12

workerIdShift = sequenceBits; // 12

datacenterIdShift = sequenceBits + workerIdBits; // 12+5 = 17

timestampLeftShift = sequenceBits + workerIdBits + datacenterIdBits; // 12+5+5 = 22

sequenceMask = -1 ^ (-1 << sequenceBits); // 4095

lastTimestamp = -1;

　　

JavaScript中Number的最大值为Number.MAX_SAFE_INTEGER：9007199254740991。在雪花算法中，有的操作在JS中会溢出，所以选用BigInt实现雪花算法。

<!DOCTYPE html>

<html lang="en">

<head>

    <meta charset="UTF-8">

    <meta name="viewport" content="width=device-width, initial-scale=1.0">

    <meta http-equiv="X-UA-Compatible" content="ie=edge">

    <title>Snowflake</title>

</head>

<body>

<script>

　　var Snowflake = (function() {

            function Snowflake(_workerId, _dataCenterId, _sequence) {

                this.twepoch = 1288834974657n;

                //this.twepoch = 0n;

                this.workerIdBits = 5n;

                this.dataCenterIdBits = 5n;

                this.maxWrokerId = -1n ^ (-1n << this.workerIdBits); // 值为：31

                this.maxDataCenterId = -1n ^ (-1n << this.dataCenterIdBits); // 值为：31

                this.sequenceBits = 12n;

                this.workerIdShift = this.sequenceBits; // 值为：12

                this.dataCenterIdShift = this.sequenceBits + this.workerIdBits; // 值为：17

                this.timestampLeftShift = this.sequenceBits + this.workerIdBits + this.dataCenterIdBits; // 值为：22

                this.sequenceMask = -1n ^ (-1n << this.sequenceBits); // 值为：4095

                this.lastTimestamp = -1n;

                //设置默认值,从环境变量取

                this.workerId = 1n;

                this.dataCenterId = 1n;

                this.sequence = 0n;

                if (this.workerId > this.maxWrokerId || this.workerId < 0) {

                    throw new Error('_workerId must max than 0 and small than maxWrokerId-[' + this.maxWrokerId + ']');

                }

                if (this.dataCenterId > this.maxDataCenterId || this.dataCenterId < 0) {

                    throw new Error('_dataCenterId must max than 0 and small than maxDataCenterId-[' + this.maxDataCenterId + ']');

                }

                this.workerId = BigInt(_workerId);

                this.dataCenterId = BigInt(_dataCenterId);

                this.sequence = BigInt(_sequence);

            }

            Snowflake.prototype.tilNextMillis = function(lastTimestamp) {

                var timestamp = this.timeGen();

                while (timestamp <= lastTimestamp) {

                    timestamp = this.timeGen();

                }

                return BigInt(timestamp);

            };

            Snowflake.prototype.timeGen = function() {

                return BigInt(Date.now());

            };

            Snowflake.prototype.nextId = function() {

                var timestamp = this.timeGen();

                if (timestamp < this.lastTimestamp) {

                    throw new Error('Clock moved backwards. Refusing to generate id for ' +

                        (this.lastTimestamp - timestamp));

                }

                if (this.lastTimestamp === timestamp) {

                    this.sequence = (this.sequence + 1n) & this.sequenceMask;

                    if (this.sequence === 0n) {

                        timestamp = this.tilNextMillis(this.lastTimestamp);

                    }

                } else {

                    this.sequence = 0n;

                }

                this.lastTimestamp = timestamp;

                return ((timestamp - this.twepoch) << this.timestampLeftShift) |

                    (this.dataCenterId << this.dataCenterIdShift) |

                    (this.workerId << this.workerIdShift) |

                    this.sequence;

            };

            return Snowflake;

        }());

        console.time();

        var tempSnowflake = new Snowflake(1n, 1n, 0n);

        var tempIds = [];

        for (var i = 0; i < 10000; i++) {

            var tempId = tempSnowflake.nextId();

            console.log(tempId);

            if (tempIds.indexOf(tempId) < 0) {

                tempIds.push(tempId);

            }

        }

        console.log(tempIds.length);

        console.timeEnd();

    </script>

</body>

</html>

　　

　　

ID生成算法(一)——雪花算法的更多相关文章

  1. 分布式系统为什么不用自增id，要用雪花算法生成id???

    1.为什么数据库id自增和uuid不适合分布式id id自增:当数据量庞大时,在数据库分库分表后,数据库自增id不能满足唯一id来标识数据:因为每个表都按自己节奏自增,会造成id冲突,无法满足需求.  ...

  2. 分布式唯一ID自增（雪花算法）

    public class IdWorker { // ==============================Fields===================================== ...

  3. 凯哥带你用python撸算法之雪花算法

    import time class Snow(object): def __init__(self, idx=None): init_date = time.strptime('2010-01-01 ...

  4. 分布式ID生成策略 · fossi

    分布式环境下如何保证ID的不重复呢?一般我们可能会想到用UUID来实现嘛.但是UUID一般可以获取当前时间的毫秒数再加点随机数,但是在高并发下仍然可能重复.最重要的是,如果我要用这种UUID来生成分表 ...

  5. 雪花算法生成ID

    前言我们的数据库在设计时一般有两个ID,自增的id为主键,还有一个业务ID使用UUID生成.自增id在需要分表的情况下做为业务主键不太理想,所以我们增加了uuid作为业务ID,有了业务id仍然还存在自 ...

  6. 分布式ID生成 - 雪花算法

    雪花算法是一种生成分布式全局唯一ID的经典算法,关于雪花算法的解读网上多如牛毛,大多抄来抄去,这里请参考耕耘的小象大神的博客ID生成器,Twitter的雪花算法(Java) 网上的教程一般存在两个问题 ...

  7. 全局唯一iD的生成 雪花算法详解及其他用法

    一.介绍 雪花算法的原始版本是scala版,用于生成分布式ID(纯数字,时间顺序),订单编号等. 自增ID:对于数据敏感场景不宜使用,且不适合于分布式场景.GUID:采用无意义字符串,数据量增大时造成 ...

  8. 全局ID生成--雪花算法

    分布式ID常见生成策略: 分布式ID生成策略常见的有如下几种: 数据库自增ID. UUID生成. Redis的原子自增方式. 数据库水平拆分,设置初始值和相同的自增步长. 批量申请自增ID. 雪花算法 ...

  9. 基于雪花算法生成分布式ID(Java版)

    SnowFlake算法原理介绍 在分布式系统中会将一个业务的系统部署到多台服务器上,用户随机访问其中一台,而之所以引入分布式系统就是为了让整个系统能够承载更大的访问量.诸如订单号这些我们需要它是全局唯 ...

随机推荐

  1. 在论坛中出现的比较难的sql问题：37(动态行转列 某一行数据转为列名)

    原文:在论坛中出现的比较难的sql问题:37(动态行转列 某一行数据转为列名) 所以,觉得有必要记录下来,这样以后再次碰到这类问题,也能从中获取解答的思路.

  2. DevExtreme学习笔记(一) DataGrid中js分析

    1.overviewjs采用 $(function() { $("#gridContainer").dxDataGrid({ dataSource: { store: { type ...

  3. pinfinder

    pinfinder https://pinfinder.net https://github.com/gwatts/pinfinder 关于 Pinfinder是一个小型免费程序,可以使用iPhone ...

  4. js 单引号和双引号相互替换的实现方法

    1.双引号替换成单引号 var domo = JSON.stringify(address).replace(/\"/g,"'"); var a = {a:1,b:2}; ...

  5. SAP-参数（条件表）配置教程–GS01/GS02/GS03

    转载:http://www.baidusap.com/abap/others/2849 在SAP开发中,某段代码运行可能需要满足某个条件,通常解决办法有两种:一种是在代码中写死限制条件,此种方式当限制 ...

  6. PX4/Pixhawk uORB

    PX4/Pixhawk的软件体系结构主要被分为四个层次 应用程序的API:这个接口提供给应用程序开发人员,此API旨在尽可能的精简.扁平及隐藏其复杂性 应用程序框架:这是为操作基础飞行控制的默认程序集 ...

  7. SSM - SpringBoot - SpringCloud

    SSM框架 Spring + Spring MVC + MyBatis:标准MVC模式 继 SSH (Struts+Spring+Hibernate)之后,主流的 Java EE企业级 Web应用程序 ...

  8. SQL SERVER-数据库备份及记录

    --完整备份 BACKUP DATABASE JINWEI TO DISK='D:\BAK\JINWEIFULL.bak' --日志备份 BACKUP LOG JINWEI TO DISK='D:\B ...

  9. 【清单】值得「等待」的12个指示加载状态的 js 库

    以下优选 GitHub 上高 star 的指示加载状态的 JavaScript 库.另外这里还有10个有意思的 JavaScript 实战小项目供大家学习. 上期入口:一份数据分析学习清单.xls M ...

  10. Linux命令——source

    参考:What does 'source' do? 前言 当我们修改了/etc/profile文件,并想让它立刻生效,而不用重新登录,就可以使用source命令,如source /etc/profil ...