loj #2319

noip2017列队 - resolve

标签：题解

---

\(n * m\) 的矩阵，每个元素 \((i, j)\) 的标号为 \((i - 1) * m + j\), 每次给出 \((x, y)\), 表示将查询此时处在 \(x\) 行 \(y\) 列元素的标号，并且删除此元素，接下来 \(x\) 行， \(y\) 列以后的元素左移，\(m\) 列，\(x\) 行以后的元素前移，显然此时 \((n, m)\) 空，将原先删除的 \((x, y)\) 元素放到 \((n, m)\)

输出每次查询

---

首先考虑一条链的情况

线段树维护 \(0 / 1\) 序列

将 \(x\) 列的元素放到最后

不考虑元素左移的情况（一条链只存在左移），这样的话如果一个元素被放到最后的位置，只需将第 \(x\) 个 \(1\) 变为 \(0\), 并且在线段树的最后的位置加入一个 \(1\), 这样的话区间的和就是区间元素的个数

列：

元素：1 2 3 4 5 6

维护：1 1 1 1 1 1

将第 3 列的数放到序列的最后

1 - 3 4 5 6 2

1 0 1 1 1 1 1

将第 3 列的数放到序列的最后

首先找到第 \(3\) 列的数，也就是第 \(3\) 个 \(1\) 的位置，此时这个位置的数为 \(4\)

1 - 3 - 5 6 2 4

1 0 1 0 1 1 1 1

推广

对每一行的前 \(m - 1\) 个元素开一颗线段树， 对最后一列开一颗线段树。

总共 \(n + 1\) 颗线段树

每颗线段树都维护这样的 \(0 / 1\) 序列代表每个位置元素的有无

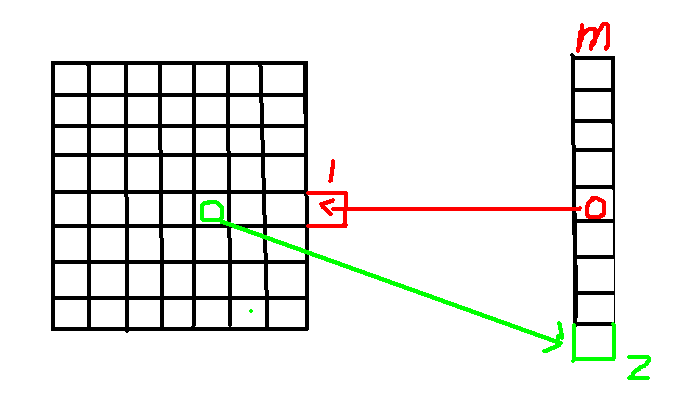
操作：

对于询问是否是 \(m\) 列的有关询问分类处理

现在需要查询绿色区域，那么就将绿色区域的元素放到2号区域，相应地，绿色区域变成 \(0\), 2号区域变成 \(1\), 然后查询 \(m\) 列 \(x\) 行的元素放到1号区域，相应地红色区域变成 \(0\)， 1号区域变为 \(1\)

如何处理元素的编号：

将每个点的编号记录下来是不可能的，这里只记录位置发生过改变的元素的编号，由于不会发生移动操作，所以没有改变的元素的编号是可以由行列的坐标得到的。只有发生元素的移动才会记录元素的编号。

对于空间

动态开节点

---

#include <bits/stdc++.h>

using namespace std;
const int N = 6e5 + 10;

int Lson[N * 30], Rson[N * 30], Size[N * 30], Root[N];
int Long[N];
int Seg;
int n, m, q;
int Len;

#define LL long long
LL Data[N * 30];

#define gc getchar()
inline int read() {int x = 0; char c = gc; while(c < '0' || c > '9') c = gc;
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = gc; return x;}
#undef gc

int now_x, now_y;

int Calc_size(int l, int r) {
	if(now_y != m) {
		if(r > Long[now_x]) return Long[now_x] - l + 1;
		else return r - l + 1;
	} else {
		if(r > Long[n + 1]) return Long[n + 1] - l + 1;
		else return r - l + 1;
	}
}

LL Ans;

void Poi_A(int &rt, int l, int r, int x) {
	if(!rt) {
		rt = ++ Seg;
		Size[rt] = Calc_size(l, r);
	}
	Size[rt] --;
	if(l == r) {
		if(Data[rt] != 0) Ans = Data[rt];
		else {
			if(now_y != m) Ans = (1ll * now_x - 1) * m + r;
			else Ans = 1ll * r * m;
		}
		return ;
	}
	int mid = (l + r) >> 1;
	int s_ = Lson[rt] ? Size[Lson[rt]] : Calc_size(l, mid);
	if(x <= s_) Poi_A(Lson[rt], l, mid, x);
	else if(Lson[rt]) Poi_A(Rson[rt], mid + 1, r, x - Size[Lson[rt]]);
	else Poi_A(Rson[rt], mid + 1, r, x - Calc_size(l, mid));
}

void Poi_G(int &rt, int l, int r, int x, LL val) {
	if(!rt) {
		rt = ++ Seg;
		Size[rt] = Calc_size(l, r);
	} else Size[rt] ++;
	if(l == r) {
		Data[rt] = val;
		return ;
	}
	int mid = (l + r) >> 1;
	if(x <= mid) Poi_G(Lson[rt], l, mid, x, val);
	else Poi_G(Rson[rt], mid + 1, r, x, val);
}

int main() {
	n = read(), m = read(), q = read();
	Len = max(n, m) + q;
	for(int i = 1; i <= n; i ++) Long[i] = m - 1;
	Long[n + 1] = n;
	for(; q; q --) {
		int xx = read(), yy = read();
		now_x = xx, now_y = yy;
		if(yy == m) {
			Poi_A(Root[n + 1], 1, Len, xx);
			cout << Ans << "\n";
			Poi_G(Root[n + 1], 1, Len, ++ Long[n + 1], Ans);
		} else {
			Poi_A(Root[xx], 1, Len, yy);
			cout << Ans << "\n";
			LL Ans1 = Ans;
			now_y = m;
			Poi_A(Root[n + 1], 1, Len, xx);
			now_y = yy;
			Poi_G(Root[xx], 1, Len, ++ Long[xx], Ans);
			now_y = m;
			Poi_G(Root[n + 1], 1, Len, ++ Long[n + 1], Ans1);
		}
	}
	return 0;
}