容器--TreeMap

一、概述

　　在Map的实现中，除了我们最常见的KEY值无序的HashMap之外，还有KEY有序的Map，比较常用的有两类，一类是按KEY值的大小有序的Map，这方面的代表是TreeMap，另外一种就保持了插入顺序的Map，这类的代表是LinkedHashMap. 本文介绍TreeMap.

　　Java提供了两种可以用来排序的接口，分别是Comparable和Comparactor, 两者分别说明如下：

　　1. Comparable

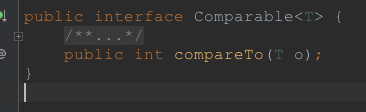
　 目前这是一个泛型接口，只有一个方法compareTo,  参与比较的类需要实现这个接口，这样该类便具备了可比较性，该方法的参数表示用来比较的对象。根据这个接口的返回值是 > 0, 小于0还是等于0决定了两个比较对象之间的大小关系。

　 如果一个类实现了这个接口，则该类的所有对象都是可比较的，也就是说，自身具备了比较的能力。JDK中的自带的一些类，比如Integer, Long等都具备比较的能力，原因就是它们实现了这个接口。

　　这种方式适合那些比较功能是类的特点之一的类，比如前面说到的Integer.

　　2. Comparator

　　除了Comparable，JDK还提供了一个接口用来比较，这就是Comparator，其接口定义如下：

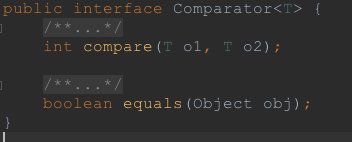
　　定义了两个方法，其中equals方法可以理解为是Object.equals的增加版本，功能和equal类似，用于比较的方法是compare, 其接收两个参数，这两个参数不需要实现任何接口，本方法负责根据一定的规则来比较两个对象的大小。

　　打个比较，这个接口的实现者好比是裁判，两个待比较的对象找它来比较大小，它根据自己定义的规则，结合两个对象的自身的数据，通过计算得出一个值，从而来决定哪个对象大哪个对象小。其本身并不参与比较。

　　有的时候待比较的对象并不需要具备可比较性，只是在某些场合下需要对它们的一个序列进行比较，或者说，可能会按多种规则对同一组序列进行比较，这个时候，用comparator构造构建器就非常合适，首先它不会侵入原类，另外，多种规则就是多个比较器，非常方便。

　　在JAVA里有关比较的下操作中，如集合排序等都提供了这两种方式的比较，我们可以根据情况进行选择。

二、实现原理分析

　　顾名思议，TreeMap的实现是基于Tree的数据结构，JAVA中可以用来排序的Tree，最有名的莫过于红黑树，而TreeMap的实现也正是基于红黑树，为了更好的理解红黑树，前面我们已经分了两篇来详细说明红黑树，在此不再细说。本文主要从各个方面分析TreeMap的构建和使用。

　　1. 创建

　　创建一个TreeMap，总共有四种方式，如下：

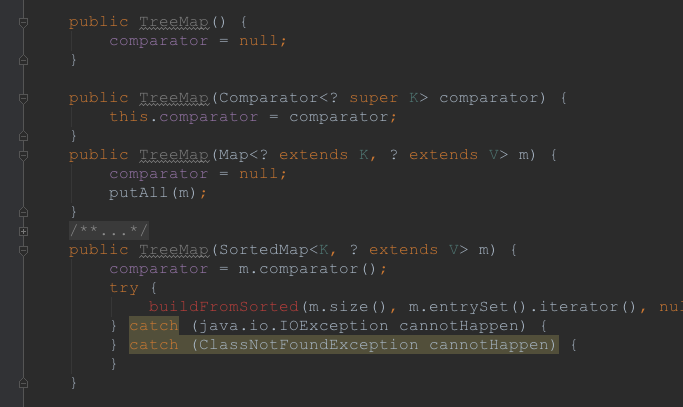
　　我们可以看到，TreeMap的这四种方式中其实主要分了两种，一是comparator为null的，一种是不为null的，作为一个有序的Map，如果comparator不为NULL，则自然是使用这个来比较，否则，KEY应该继承Comparable接口，这个也是前面解释过的。

　　作为一个红黑树，那么整个数据的存储则必是一颗树，TreeMap的实现也遵守了这一点，我们可以看一下对于树的构造。

　　首先，有一个表示根节点的变量。

　　

　　其次，我们看一下节点的定义，也具备红黑树节点的性质

　　

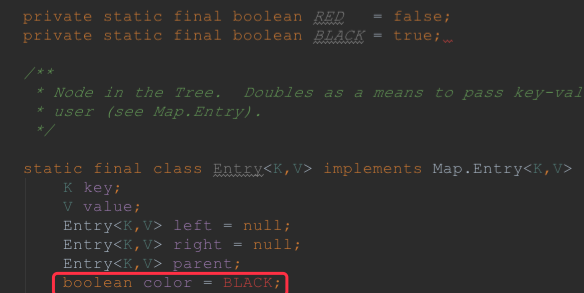
　　可以看到节点的定义中除了有key和value之外，还有左孩子，右孩子，父节点，以及节点的颜色，根据这三个属性，我们可以很方便的从任何一个节点向上一级或者向下一级导航。通过对节点设置颜色，很容易实现红黑树的相关算法。

　　2. 添加

　　添加指添加一个新节点到树的合适位置。那么这个分类两个部分，首先是要找到合适的节点，这个可以通过二叉树的查找算法来完成，查找之后有两个结果，如果找到相同的KEY了，则做更新操作，如果没有找到，则需要把节点和原来的树关联，关联之后，由于可能会破坏红黑树的性质，所以还要根据情况再做一次调整。

　　具体的算法如下：

　　

 public V put(K key, V value) {
         Entry<K,V> t = root;
         if (t == null) {
             compare(key, key); // type (and possibly null) check

             root = new Entry<>(key, value, null);
             size = 1;
             modCount++;
             return null;
         }
         int cmp;
         Entry<K,V> parent;
         // split comparator and comparable paths
         Comparator<? super K> cpr = comparator;
         if (cpr != null) {
             do {
                 parent = t;
                 cmp = cpr.compare(key, t.key);
                 if (cmp < 0)
                     t = t.left;
                 else if (cmp > 0)
                     t = t.right;
                 else
                     return t.setValue(value);
             } while (t != null);
         }
         else {
             if (key == null)
                 throw new NullPointerException();
             Comparable<? super K> k = (Comparable<? super K>) key;
             do {
                 parent = t;
                 cmp = k.compareTo(t.key);
                 if (cmp < 0)
                     t = t.left;
                 else if (cmp > 0)
                     t = t.right;
                 else
                     return t.setValue(value);
             } while (t != null);
         }
         Entry<K,V> e = new Entry<>(key, value, parent);
         if (cmp < 0)
             parent.left = e;
         else
             parent.right = e;
         fixAfterInsertion(e);
         size++;
         modCount++;
         return null;
     }

　　上面的代码就是整个添加的过程，关键的地方进行了加粗显示，可以看到，在查找的时候，实现时根据比较器是否存在来决定采用哪一种方式进行比较，如果比较之后没有找到对应的节点，则parent变量记录了最后一个不为叶子节点的节点，该节点即为新节点的父节点。新增后，需要对树重新做调整。

　　调整算法已经在红黑树部分介绍过了，所以这里就不再细说。

　　3. 删除

　　删除的话同样也是先通过二叉树的查找算法找到对应的节点，如果节点有两个孩子节点，则需要进一步查找其直接后继，然后针对其后继节点做删除操作。这样可以保证被删除的元素只有最多不超过一个节点。

　　删除完成后，根据被删除节点的后继节点的情况做相应的删除修复操作，以保证删除后，原树还是一个红黑树，删除的完整代码如下：

private void deleteEntry(Entry<K,V> p) {
        modCount++;
        size--;

        // If strictly internal, copy successor's element to p and then make p
        // point to successor.
        if (p.left != null && p.right != null) {
            Entry<K,V> s = successor(p);
            p.key = s.key;
            p.value = s.value;
            p = s;
        } // p has 2 children

        // Start fixup at replacement node, if it exists.
        Entry<K,V> replacement = (p.left != null ? p.left : p.right);

        if (replacement != null) {
            // Link replacement to parent
            replacement.parent = p.parent;
            if (p.parent == null)
                root = replacement;
            else if (p == p.parent.left)
                p.parent.left  = replacement;
            else
                p.parent.right = replacement;

            // Null out links so they are OK to use by fixAfterDeletion.
            p.left = p.right = p.parent = null;

            // Fix replacement
            if (p.color == BLACK)
                fixAfterDeletion(replacement);
        } else if (p.parent == null) { // return if we are the only node.
            root = null;
        } else { //  No children. Use self as phantom replacement and unlink.
            if (p.color == BLACK)
                fixAfterDeletion(p);

            if (p.parent != null) {
                if (p == p.parent.left)
                    p.parent.left = null;
                else if (p == p.parent.right)
                    p.parent.right = null;
                p.parent = null;
            }
        }
    }

　　修复的操作在前面的红黑树中已经介绍了，就不再详细分析了。

　　4. 遍历操作

　　和普通的Map相比，作为一个排序Map，TreeMap也提供了各种遍历的操作，如headMap, tailMap,descendingMap等，我们可以方便的进行正序或倒序的遍历，这得益于节点的双向关联。在此不再一一描述

三、总结

　　至此，基于红黑数的TreeMap就算是完全分析完了，这是一种很经典的实现，通过对其源码的分析我们可以更深刻的理解红黑树，也可以学习到一些好的设计思想。同时，也有助于我们正确地使用红黑树