xDeepFM

1. xDeepFM优势

　　自动高效的学习隐式和显示的高维特征交互

　　设计一个新的CIN网络可以显示学习高阶特征交互，且为Vector-Wise

2. xDeepFM整体算法框架 

　　　　　　　　 

　　整个网络结构主要分为两部分：压缩交互网络和DNN网络。压缩交互网络主要是实现自动学习显示的高阶特征交互，DNN网络主要是实现隐式的学习高阶特征。

3. 压缩交互网络（Compressed Interaction Network,CIN）

　　CIN中每一层的神经元都是根据前一层的隐层及原特征向量计算而来，其数学表达式为：

　                                             　

　　其整个过程分为两步：

　　　　利用前一层的隐层状态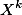和原始特征矩阵，计算出中间结果，其维度为三维。

　　　　CIN卷积操作，Feature Map为向量而非矩阵

　　　　　　　　　　

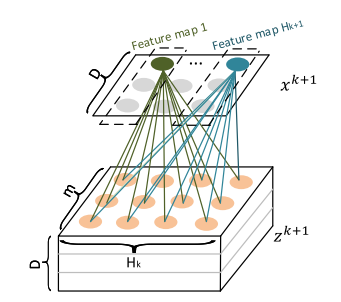
　　　　每一层隐层都是通过一个池化操作连接到输出层

　　　　　　　　　　　　

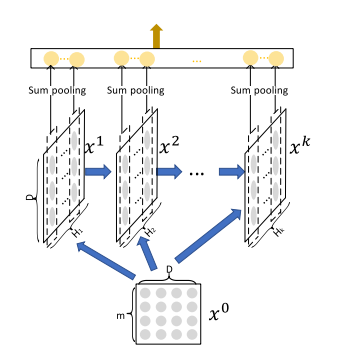
 4. 参考博客

　　https://zhuanlan.zhihu.com/p/83784018

https://daiwk.github.io/posts/dl-dl-ctr-models.html