剑指offer4：重建二叉树（后序遍历）

1. 题目描述

　　输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

2. 思路和方法

　　（1）先序遍历序列的第一个元素必定是根节点，可以由此获取二叉树的根节点。

　　（2）根据根节点，中序遍历序列中查找该节点，由中序遍历的性质可知，中序遍历中该根节点左边的序列必定在根节点的左子树中，根节点右边的序列必定在右子树中。由此可以知道先序遍历中左子树以及右子树的起止位置。

　　（3）分别对左子树和右子树重复上述的过程，直至所有的子树的起止位置相等时，说明已经到达叶子节点，遍历完毕。
　　（4）先序+中序->后序，中序+后序->先序，层次+中序->。

例子：

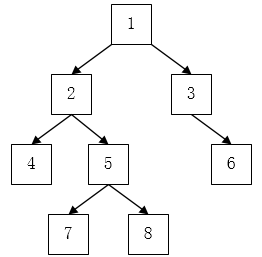
　　先序遍历：1 2 4 5 7 8 3 6 （根左右）

　　中序遍历：4 2 7 5 8 1 3 6（左根右）

　　后序遍历：4 7 8 5 2 6 3 1（左右根）

　　层次遍历：1 2 3 4 5 6 7 8 （共4层，与广度搜索一样，即广度遍历）

特殊例子：

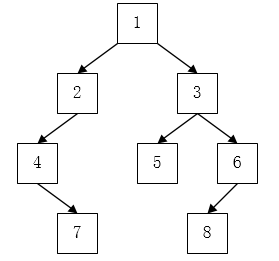
先序遍历：1, 2, 4, 7, 3, 5, 6, 8 （根左右）

中序遍历：4, 7, 2, 1, 5, 3, 8, 6 （左根右）

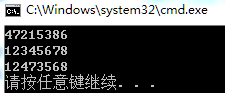
后序遍历：7 4 2 5 8 6 3 1（左右根）

层次遍历：1 2 3 4 5 6 7 8 （共4层，与广度搜索一样，即广度遍历）

3. 核心代码

 /**

  * Definition for binary tree

  * struct TreeNode {

  *     int val;

  *     TreeNode *left;

  *     TreeNode *right;

  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}

  * };

  */

 class Solution {

 public:

     TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {

         int len=vin.size();

         if (len==)

             return NULL;

         vector<int> left_pre,right_pre,left_vin,right_vin;

         TreeNode* head = new TreeNode(pre[]);

         int gen = ;

         for(int i=;i<len;i++)

         {

             if(vin[i]==pre[])

             {

                 gen = i;

                 break;

             }

         }

         for(int i=;i<gen;i++)

         {

             left_pre.push_back(pre[i+]);

             left_vin.push_back(vin[i]);

         }

         for(int i=gen+;i<len;i++)

         {

             right_pre.push_back(pre[i]);

             right_vin.push_back(vin[i]);

         }

         head->left = reConstructBinaryTree(left_pre,left_vin);

         head->right = reConstructBinaryTree(right_pre,right_vin);

         return head;

     }

 };

4. C++完整实现

 #include <vector>

 #include <iostream>

 #include <string>

 #include <stdlib.h>

 #include <algorithm>

 using namespace std;

 struct TreeNode {

     int val;

     TreeNode *left;

     TreeNode *right;

     TreeNode(int x) :val(x), left(nullptr), right(nullptr) {}

 } ;

 //打印节点/访问函数

 void PrintNode(TreeNode* T)

 {

     if (T->val != -)

         cout << T->val << " ";

 }

 //先序遍历

 void PreOrder(TreeNode* T)

 {

     if (T != NULL)

     {

         //访问根节点

         PrintNode(T);

         //访问左子结点

         PreOrder(T->left);

         //访问右子结点

         PreOrder(T->right);

     }

 }

 //中序遍历

 void InOrder(TreeNode* T)

 {

     if (T != NULL)

     {

         //访问左子结点

         InOrder(T->left);

         //访问根节点

         PrintNode(T);

         //访问右子结点

         InOrder(T->right);

     }

 }

 //后序遍历

 void PostOrder(TreeNode* T)

 {

     if (T != NULL)

     {

         //访问左子结点

         PostOrder(T->left);

         //访问右子结点

         PostOrder(T->right);

         //访问根节点

         PrintNode(T);

     }

 }

 TreeNode* reConstructBinaryTree(vector<int> pre, vector<int> vin)

 {

     if (pre.size() ==  || pre.size() != vin.size())

         return nullptr;

     TreeNode *newNode = new TreeNode(pre[]);

     //如果只剩一个节点了，那么可以直接返回

     if (pre.size() == )

         return newNode;

     auto posi = find(vin.begin(), vin.end(), pre[]);

     //错误检测

     if (posi == vin.end()) {

         return nullptr;

     }

     int leftSize = posi - vin.begin();

     int rightSize = vin.end() - posi - ;

     //递归求解

     //这里取前序和后序遍历的左右子树可能有点绕，可以好好思考一下

     newNode->left = reConstructBinaryTree(vector<int>(pre.begin() + , pre.begin() +  + leftSize),

         vector<int>(vin.begin(), vin.begin() + leftSize));

     newNode->right = reConstructBinaryTree(vector<int>(pre.begin() +  + leftSize, pre.end()),

         vector<int>(vin.begin() + leftSize + , vin.end()));

     return newNode;

 }

 int main()

 {

     vector<int> pre{ , , , , , , ,  };

     vector<int> vin{ , , , , , , ,  }; ////7 4 2 5 8 6 3 1

     TreeNode *posTraversal = reConstructBinaryTree(pre, vin);

     cout << "后序遍历：";

     PostOrder(posTraversal);

     cout << endl;

     cout << "先序遍历：";

     PreOrder(posTraversal);

     cout << endl;

     cout << "先序遍历：";

     InOrder(posTraversal);

     cout << endl;

     system("pause");

     return ;

 }

5 扩展

5.1 给出中序和后序，得到二叉树

后序和先序（左右根，根左右），因此后序的根的位置为pos[pos.size()-1].

main函数中的代码如下：

cout << "给出中序和后序，构建二叉树" << endl;
//vector<int> pre{ 1, 2, 4, 7, 3, 5, 6, 8 };

vector<int> vin1{ 4, 7, 2, 1, 5, 3, 8, 6 };

vector<int> pos1{ 7, 4, 2, 5, 8, 6, 3, 1 };

TreeNode* preTraversal = reConstructBinaryTree1(pos1, vin1);

cout << "中序遍历：";

InOrder(preTraversal);

cout << endl;

C++核心代码

 TreeNode* reConstructBinaryTree1(vector<int> pos, vector<int> vin)

 {

     if (pos.size() ==  || pos.size() != vin.size())

         return nullptr;

     int poslen = pos.size();

     TreeNode *newNode = new TreeNode(pos[poslen-]);

     //如果只剩一个节点了，那么可以直接返回

     if (poslen == )

         return newNode;

     auto posi = find(vin.begin(), vin.end(), pos[poslen-]);

     if (posi == vin.end())

         return nullptr;

     int leftSize = posi - vin.begin();

     int rightSize = vin.end() - posi - ;

     newNode->left = reConstructBinaryTree1(vector<int>(pos.begin(), pos.begin() + leftSize), vector<int>(vin.begin(), vin.begin() + leftSize));

     newNode->right = reConstructBinaryTree1(vector<int>(pos.begin() + leftSize, pos.end()-), vector<int>(vin.begin() + leftSize + , vin.end()));

     return newNode;

 }

5.2 给出中序和层次构建二叉树

参考资料：https://blog.csdn.net/yanyanwenmeng/article/details/77833274（一般C++程序）

参考资料：https://blog.csdn.net/sinat_30324577/article/details/82688414（Python）

核心思想：对于子树，其在层次遍历最前面的点即为根节点，故重建过程包括以下两步：
1.利用层次遍历确定子树的根节点；
2.根据根节点在中序中的位置划定左右子树，递归重建。

一般C++程序

 #include<iostream>

 #include<string>

 using namespace std;

 string s1, s2;

 void calc(int l1, int r1, int l2, int r2)

 {

     int i, j;

     for (i = l2; i <= r2; i++)//找层次遍历中优先输出根节点的位置

     {

         int b = ;

         for (j = l1; j <= r1; j++)

         {

             if (s2[i] == s1[j])

             {

                 cout << s1[j];//输出根节点

                 b = ;

                 break;

             }

         }

         if (b) break;

     }

     if (j>l1) calc(l1, j - , , r2);//遍历左子树

     if (j<r1) calc(j + , r1, , r2);//遍历右子树

 }

 int main()

 {

     cin >> s1 >> s2;

     calc(, s1.length() - , , s2.length() - );

     cout << endl;

     return ;

 }

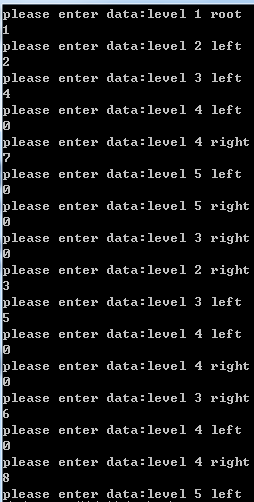
运行：输入输出

C++核心程序（vector<int>）

 TreeNode* reConstructBinaryTree2(vector<int> level, vector<int> vin)

 {

     if (level.size() ==  || vin.size() == )

         return nullptr;

     vector<int> lst;

     for (int i = ; i < vin.size(); i++){

         lst.push_back(find(level.begin(), level.end(), vin[i]) - level.begin());

     }

     int minPosition = min_element(lst.begin(), lst.end()) - lst.begin();

     cout << "vin[minPosition]=" << vin[minPosition] << endl;

     TreeNode *newNode = new TreeNode(vin[minPosition]);

     newNode->left = reConstructBinaryTree2(vector<int>(level.begin(), level.end()),

         vector<int>(vin.begin(), vin.begin() + minPosition));

     newNode->right = reConstructBinaryTree2(vector<int>(level.begin(), level.end()),

         vector<int>(vin.begin() + minPosition + , vin.end()));

     return newNode;

 ｝

输出：

6. 二叉树构建参考资料：用先序构建，https://blog.csdn.net/u014453898/article/details/54894796

C++代码

 #include<iostream>

 #include<string>

 using namespace std;

 /*二叉树的结构体*/

 typedef struct BTree

 {

     int val;

     struct BTree *left, *right;

 }BTree;

 /*二叉树的类，包含着操作二叉树的各种方法*/

 class Tree

 {

 public:

     BTree *create_node(int level, string pos);

     void PreOrder(BTree *t);  //先序遍历

     void InOrder(BTree *t);  //中序遍历

     void PostOrder(BTree *t);  //后序遍历 

     BTree *root;

 };

 /*用先序遍历的方法递归构造一课二叉树*/

 BTree* Tree::create_node(int level, string pos)

 {

     int data;

     BTree *node = new BTree;

     cout << "please enter data:level " << level << " " << pos << endl;

     cin >> data;

     //若输入的数据为0，则把该结点的子结点置为空

     if (data == )

     {

         return NULL;

     }

     node->val = data;

     /*create_node（）的    参数用于在给二叉树赋值时表明

     现在赋值的是哪个结点*/

     node->left = create_node(level + , "left");

     node->right = create_node(level + , "right");

     return node;

 }

 void Tree::PreOrder(BTree *t)

 {

     if (t)

     {

         cout << t->val << endl;;

         PreOrder(t->left);

         PreOrder(t->right);

     }

 }

 void Tree::InOrder(BTree *t)

 {

     if (t)

     {

         InOrder(t->left);

         cout << t->val << endl;;

         InOrder(t->right);

     }

 }

 void Tree::PostOrder(BTree *t)

 {

     if (t)

     {

         PostOrder(t->left);

         PostOrder(t->right);

         cout << t->val << endl;

     }

 }

 int main()

 {

     Tree tree;

     tree.root = tree.create_node(, "root");

     cout << "Pre" << endl;

     tree.PreOrder(tree.root);

     cout << "In" << endl;

     tree.InOrder(tree.root);

     cout << "Post" << endl;

     tree.PostOrder(tree.root);

     system("pause");

     return ;

 }

7. 完整C++程序

 #include <vector>

 #include <iostream>

 #include <string>

 #include <stdlib.h>

 #include <algorithm>

 using namespace std;

 struct TreeNode {

     int val;

     TreeNode *left;

     TreeNode *right;

     TreeNode(int x) :val(x), left(nullptr), right(nullptr) {}

 };

 //打印节点/访问函数

 void PrintNode(TreeNode* T)

 {

     if (T->val != -)

         cout << T->val << " ";

 }

 //先序遍历

 void PreOrder(TreeNode* T)

 {

     if (T != NULL)

     {

         //访问根节点

         PrintNode(T);

         //访问左子结点

         PreOrder(T->left);

         //访问右子结点

         PreOrder(T->right);

     }

 }

 //中序遍历

 void InOrder(TreeNode* T)

 {

     if (T != NULL)

     {

         //访问左子结点

         InOrder(T->left);

         //访问根节点

         PrintNode(T);

         //访问右子结点

         InOrder(T->right);

     }

 }

 //后序遍历

 void PostOrder(TreeNode* T)

 {

     if (T != NULL)

     {

         //访问左子结点

         PostOrder(T->left);

         //访问右子结点

         PostOrder(T->right);

         //访问根节点

         PrintNode(T);

     }

 }

 TreeNode* reConstructBinaryTree(vector<int> pre, vector<int> vin)

 {

     if (pre.size() ==  || pre.size() != vin.size())

         return nullptr;

     TreeNode *newNode = new TreeNode(pre[]);

     //如果只剩一个节点了，那么可以直接返回

     if (pre.size() == )

         return newNode;

     auto posi = find(vin.begin(), vin.end(), pre[]);

     if (posi == vin.end())

         return nullptr;

     int leftSize = posi - vin.begin();

     int rightSize = vin.end() - posi - ;

     newNode->left = reConstructBinaryTree(vector<int>(pre.begin() + , pre.begin() +  + leftSize),

         vector<int>(vin.begin(), vin.begin() + leftSize));

     newNode->right = reConstructBinaryTree(vector<int>(pre.begin() +  + leftSize, pre.end()),

         vector<int>(vin.begin() + leftSize + , vin.end()));

     return newNode;

 }

 TreeNode* reConstructBinaryTree1(vector<int> pos, vector<int> vin)

 {

     if (pos.size() ==  || pos.size() != vin.size())

         return nullptr;

     int poslen = pos.size();

     TreeNode *newNode = new TreeNode(pos[poslen - ]);

     //如果只剩一个节点了，那么可以直接返回

     if (poslen == )

         return newNode;

     auto posi = find(vin.begin(), vin.end(), pos[poslen - ]);

     if (posi == vin.end())

         return nullptr;

     int leftSize = posi - vin.begin();

     int rightSize = vin.end() - posi - ;

     newNode->left = reConstructBinaryTree1(vector<int>(pos.begin(), pos.begin() + leftSize), vector<int>(vin.begin(), vin.begin() + leftSize));

     newNode->right = reConstructBinaryTree1(vector<int>(pos.begin() + leftSize, pos.end() - ), vector<int>(vin.begin() + leftSize + , vin.end()));

     return newNode;

 }

 TreeNode* reConstructBinaryTree2(vector<int> level, vector<int> vin)

 {

     if (level.size() ==  || vin.size() == )

         return nullptr;

     vector<int> lst;

     for (int i = ; i < vin.size(); i++){

         lst.push_back(find(level.begin(), level.end(), vin[i]) - level.begin());

     }

     int minPosition = min_element(lst.begin(), lst.end()) - lst.begin();

     //cout << "vin[minPosition]=" << vin[minPosition] << endl;

     TreeNode *newNode = new TreeNode(vin[minPosition]);

     newNode->left = reConstructBinaryTree2(vector<int>(level.begin(), level.end()),

         vector<int>(vin.begin(), vin.begin() + minPosition));

     newNode->right = reConstructBinaryTree2(vector<int>(level.begin(), level.end()),

         vector<int>(vin.begin() + minPosition + , vin.end()));

     return newNode;

 //if not level or not vin :

 //return None

 //lst = []

 //for num in vin :

 //    lst.append(level.index(num))

 //idx = lst.index(min(lst))

 //

 //root = TreeNode(vin[idx])

 //left = vin[0:idx]

 //right = vin[idx + 1:]

 //root.left = restruct(level, left)

 //root.right = restruct(level, right)

 //return root

 }

 int main()

 {

     //层次遍历是1 2 3 4 5 6 7 8

     cout << "给出先序和中序，构建二叉树" << endl;

     vector<int> pre0{ , , , , , , ,  };

     vector<int> vin0{ , , , , , , ,  }; ////7 4 2 5 8 6 3 1

     TreeNode* posTraversal = reConstructBinaryTree(pre0, vin0);

     cout << "后序遍历：";

     PostOrder(posTraversal);

     cout << endl;

     cout << "先序遍历：";

     PreOrder(posTraversal);

     cout << endl;

     cout << "中序遍历：";

     InOrder(posTraversal);

     cout << endl;

     cout << "给出中序和后序，构建二叉树" << endl;

     //vector<int> pre{ 1, 2, 4, 7, 3, 5, 6, 8 };

     vector<int> vin1{ , , , , , , ,  };

     vector<int> pos1{ , , , , , , ,  };

     TreeNode* preTraversal = reConstructBinaryTree1(pos1, vin1);

     cout << "后序遍历：";

     PostOrder(preTraversal);

     cout << endl;

     cout << "先序遍历：";

     PreOrder(preTraversal);

     cout << endl;

     cout << "中序遍历：";

     InOrder(preTraversal);

     cout << endl;

     cout << "给出中序和层次，构建二叉树" << endl;

     //vector<int> pre{ 1, 2, 4, 7, 3, 5, 6, 8 };

     //vector<int> pos1{ 7, 4, 2, 5, 8, 6, 3, 1 };

     vector<int> level2{ , , , , , , ,  };

     vector<int> vin2{ , , , , , , ,  };

     TreeNode* Traversal = reConstructBinaryTree2(level2, vin2);

     cout << "后序遍历：";

     PostOrder(Traversal);

     cout << endl;

     cout << "先序遍历：";

     PreOrder(Traversal);

     cout << endl;

     cout << "中序遍历：";

     InOrder(Traversal);

     cout << endl;

     system("pause");

     return ;

 }

 //class TreeNode : # 定义二叉树节点类

 //    def __init__(self, val) :

 //    self.val = val

 //    self.left = None

 //    self.right = None

 //

 //    def restruct(level, vin) :

 //if not level or not vin :

 //return None

 //lst = []

 //    for num in vin :

 //    lst.append(level.index(num))

 //        print("lst" + str(lst))

 //        idx = lst.index(min(lst))

 //        print("idx--" + str(idx))

 //

 //        root = TreeNode(vin[idx])

 //        left = vin[0:idx]

 //        right = vin[idx + 1:]

 //        root.left = restruct(level, left)

 //        root.right = restruct(level, right)

 //        return root

 //

 //        lst1 = []

 //        lst2 = []

 //

 //        def pre_traverse(root) :

 //    if not root :

 //    return None

 //        lst1.append(root.val)

 //        pre_traverse(root.left)

 //        pre_traverse(root.right)

 //        return lst1

 //

 //        def leaf(root) :

 //    if not root :

 //    return None

 //    if not root.left and not root.right :

 //        lst2.append(root.val)

 //        leaf(root.left)

 //        leaf(root.right)

 //        return lst2

 //

 //        b = restruct([1, 2, 3, 4, 5, 6, 7, 8], [4, 7, 2, 1, 5, 3, 8, 6])

 //

 //        print(pre_traverse(b))

参考资料

https://blog.csdn.net/My_Jobs/article/details/43451187

https://blog.csdn.net/wtyvhreal/article/details/45644843

https://blog.csdn.net/m0_37950361/article/details/82531649

https://blog.csdn.net/u014453898/article/details/54894796

https://blog.csdn.net/sinat_30324577/article/details/82688414