B树，B+树的原理及区别

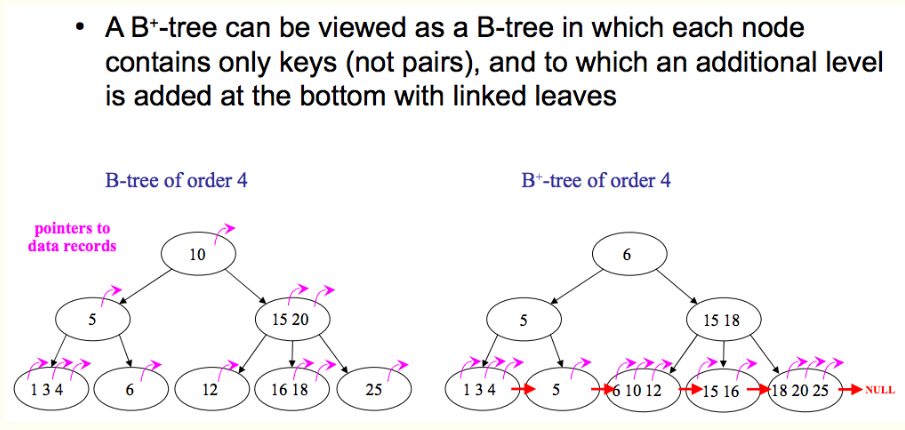
如图所示，区别有以下两点：

　　1. B+树中只有叶子节点会带有指向记录的指针（ROWID），而B树则所有节点都带有，在内部节点出现的索引项不会再出现在叶子节点中。

　　2. B+树中所有叶子节点都是通过指针连接在一起，而B树不会。

B树的原理：

　　就是为了存储设备或者磁盘设计的一种平衡查找树；通过对树高度的降低可以提升查找效率，尤其是在大量数据进行存储的时候会存储到外部磁盘，通过对外部磁盘的读取时需要快速的查找到对应的位置，所以需要一种高效的外村数据结构。

B树的优点：

　　对于在内部节点的数据，可直接得到，不必根据叶子节点来定位。

B+树的原理：

　　B+树是B树的一种变形，它把数据都存储在叶子节点，内部只存关键字（其中叶子节点的最小值作为索引）和孩子指针，简化了内部节点；B+树的遍历高效，将所以叶子节点串联成链表即可从头到尾遍历，

B+树的优点：

　　1. 非叶子节点不会带上ROWID，这样，一个块中可以容纳更多的索引项，一是可以降低树的高度。二是一个内部节点可以定位更多的叶子节点。

　　2. 叶子节点之间通过指针来连接，范围扫描将十分简单，而对于B树来说，则需要在叶子节点和内部节点不停的往返移动。

为什么B+树比B树更适合做系统的数据库索引和文件索引
1）B+树的磁盘读写代价更低
因为B+树内部结点没有指向关键字具体信息的指针，内部结点相对B树小
2）B+树的查询更加稳定
因为非终端结点并不是指向文件内容的结点，仅仅是作为叶子结点的关键字索引，因此所有的关键字查询都会走一条从根节点到叶子结点的路径。即s所有关键字查询的长度是一样的，查询效率稳定。