IDEA 2019中一些有偏好设置
1.取消启动时自动进入上一次工程:
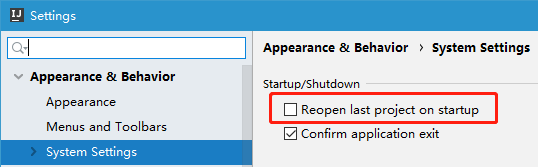
路径:Setting ——> Appearance & Behavior ——> System Setting
取消勾选Reopen last project on startup
IDEA 2019中一些有偏好设置的更多相关文章
- iOS开发之数据存储之Preference(偏好设置)
1.概述 很多iOS应用都支持偏好设置,比如保存用户名.密码.字体大小等设置,iOS提供了一套标准的解决方案来为应用加入偏好设置功能. 每个应用都有个NSUserDefaults实例,通过它来存取偏好 ...
- Xcode6与Xcode5中沙盒的变动以及偏好设置目录的变动
1.Xcode6模拟器路径与Xcode5模拟器路径对比: (1)Xcode5中模拟器路径为:/Users/用户名/Library/Application Support/iPhone Simulato ...
- iOS中偏好设置的创建,数据写入与读取
NSUserDefaults与NSDictinary? 应用通过NSUserDefaults用键值对的方式来读取和保存偏好设置数据,与通过键从NSDictionary对象中获取数据一样,不同之处在于N ...
- MongoDB 读偏好设置中增加最大有效延迟时间的参数
在某些情况下,将读请求发送给副本集的备份节点是合理的,例如,单个服务器无法处理应用的读压力,就可以把查询请求路由到可复制集中的多台服务器上.现在绝大部分MongoDB驱动支持读偏好设置(read pr ...
- iOS-数据持久化-偏好设置
一.简单介绍 很多iOS应用都支持偏好设置,比如保存用户名.密码.字体大小等设置,iOS提供了一套标准的解决方案来为应用加入偏好设置功能 每个应用都有个NSUserDefaults实例,通过它来存取偏 ...
- 持久化存储——偏好设置,plist,归档---学习笔记二
//一. 本地持久化 //1.沙盒 //1.1 应用程序包:存放的是应用程序的源文件,包括资源文件和可执行文件 NSString *path = [[NSBundle mainBundle]bundl ...
- iOS开发——UI进阶篇(十一)应用沙盒,归档,解档,偏好设置,plist存储,NSData,自定义对象归档解档
1.iOS应用数据存储的常用方式XML属性列表(plist)归档Preference(偏好设置)NSKeyedArchiver归档(NSCoding)SQLite3 Core Data 2.应用沙盒每 ...
- iOS数据持久化文件读写之偏好设置
很多iOS应用都支持偏好设置,比如保存用户名.密码.字体大小等设置,iOS提供了一套标准的解决方案来为应用加入偏好设置功能.每个应用都有个NSUserDefaults实例,通过它来存取偏好设置.比如, ...
- IOS第13天(2,私人通讯录,plist存储,偏好设置,归档)
***************plist存储 // 当点点击保存的时候调用 //保存 - (IBAction)save:(id)sender { // 获取沙盒的根路径 // NSString *ho ...
随机推荐
- log4j2 日志打两遍的问题
在使用log4j2的时候,一般都需要不同的日志分类打印不同的日志等级,如下面的配置 <!-- 用于指定log4j自动重新配置的监测间隔时间,单位是秒 --> <configurati ...
- 二叉堆的应用——查找长度为N数组中第M大数
看到这个题目首先想到是排序,那么时间复杂度自然就是O(NlgN).那么使用二叉堆如何解决呢? 对于下面一个数组,共有12个元素,我们的目标就是找出第5大元素——12 首先建立一个具有M个元素的最小堆, ...
- Java笔记(基础第四篇)
Java集合类 集合类概述 Java 语言的java.util包中提供了一些集合类,这些集合类又被称为容器.常用的集合有List集合.Set集合.Map集合,其中List与Set实现了Collecti ...
- ubuntu系统升级PHP版本
https://blog.csdn.net/qq_16885135/article/details/79747045 升级PHP7.2 https://www.cnblogs.com/lalal ...
- PHP mysqli_num_rows() 函数
<?php // 假定数据库用户名:root,密码:123456,数据库:RUNOOB $con=mysqli_connect("localhost","root& ...
- Can't load Microsoft.ReportViewer.ProcessingObjectModel.dll
本机的时候是能正常看到report,但deploy到别的机器上却不行,按说从本机拷个dll过去就可以,但怎么也找不到. 原来要在cmd那里输入C:\WINDOWS\assembly\GAC_MSIL ...
- java实现上传文件夹
我们平时经常做的是上传文件,上传文件夹与上传文件类似,但也有一些不同之处,这次做了上传文件夹就记录下以备后用. 首先我们需要了解的是上传文件三要素: 1.表单提交方式:post (get方式提交有大小 ...
- HGOI 20191031am 题解
Problem A Divisors 给出$m$个不同的正整数$a_i$,设数论函数 $f(k) = \sum\limits_{i = 1}^{n} [(\sum\limits_{j = 1}^ ...
- 5.使用Ribbon实现客户端侧负载均衡
Ribbon实现客户端侧负载均衡 5.1. Ribbon简介 Ribbon是Netflix发布的开源项目,主要功能是提供客户端的软件负载均衡算法 ...
- Leetcode题目53.最大子序和(动态规划-简单)
题目描述: 给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和. 示例: 输入: [-2,1,-3,4,-1,2,1,-5,4],输出: 6解释: 连 ...
