poj 1279 -- Art Gallery (半平面交)
鏈接:http://poj.org/problem?id=1279
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 5337 | Accepted: 2277 |
Description
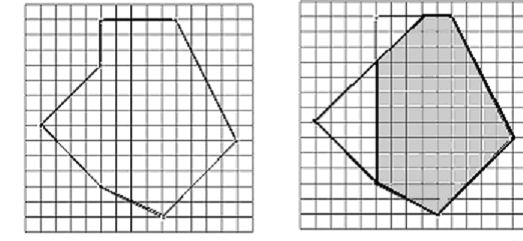
Input
Output
Sample Input
1
7
0 0
4 4
4 7
9 7
13 -1
8 -6
4 -4
Sample Output
80.00
Source
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm> #define eps 1e-8
#define MAXX 1510 typedef struct point
{
double x;
double y;
}point; point p[MAXX],s[MAXX]; using namespace std;
bool dy(double x,double y)
{
return x>y+eps;
}
bool xy(double x,double y)
{
return x<y-eps;
}
bool dyd(double x,double y)
{
return x>y-eps;
}
bool xyd(double x,double y)
{
return x<y+eps;
}
bool dd(double x,double y)
{
return fabs(x-y)<eps;
} double crossProduct(point a,point b,point c)
{
return (c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x);
} point IntersectPoint(point u1,point u2,point v1,point v2)
{
point ans=u1;
double t = ((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x))/
((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x));
ans.x += (u2.x-u1.x)*t;
ans.y += (u2.y-u1.y)*t;
return ans;
} double Area(point p[],int n)
{
double ans=0.0;
for(int i=; i<n-; i++)
{
ans += crossProduct(p[],p[i],p[i+]);
}
return fabs(ans)/2.0;
} double dist(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
} bool cmp(point a,point b)
{
double tmp=crossProduct(p[],a,b);
if(dd(tmp,0.0))
return dy(dist(p[],a),dist(p[],b));
return xy(tmp,0.0);
} point Getsort(int n)
{
int tmp=;
for(int i=; i<n; i++)
{
if(xy(p[i].x,p[tmp].x) || dd(p[i].x,p[tmp].x)&&xy(p[i].y,p[tmp].y))
{
tmp=i;
}
}// printf("%d^^",tmp);
swap(p[],p[tmp]);
sort(p+,p+n,cmp);
} void cut(point p[],point s[],int n,int &len)
{
point tp[MAXX];
p[n]=p[];
for(int i=; i<=n; i++)
{
tp[i]=p[i];
}
int cp=n,tc;
for(int i=; i<n; i++)
{
tc=;
for(int k=; k<cp; k++)
{
if(xyd(crossProduct(p[i],p[i+],tp[k]),0.0))
s[tc++]=tp[k];
if(xy(crossProduct(p[i],p[i+],tp[k])*
crossProduct(p[i],p[i+],tp[k+]),0.0))
s[tc++]=IntersectPoint(p[i],p[i+],tp[k],tp[k+]);
}
s[tc]=s[];
for(int k=; k<=tc; k++)
tp[k]=s[k];
cp=tc;
}
len=cp;
} int main()
{
int t,n,m,i,j;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=; i<n; i++)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
}
//point tmp=IntersectPoint(p[0],p[1],p[2],p[3]);
//printf("%lf %lf\n",tmp.x,tmp.y);
Getsort(n);//for(i=0; i<n; i++)printf("%lf**%lf*\n",p[i].x,p[i].y);
int len;
cut(p,s,n,len);//for(i=0; i<len; i++)printf("%lf==%lf=\n",s[i].x,s[i].y);
double area=Area(s,len);
printf("%.2lf\n",area);
}
return ;
}
利用面积正负来判断顺or逆,这种代码是以逆时针为主,我的面积顺时针为正,
需要改变方向
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm> #define eps 1e-8
#define MAXX 1510 typedef struct point
{
double x;
double y;
}point; point p[MAXX],s[MAXX]; using namespace std;
bool dy(double x,double y)
{
return x>y+eps;
}
bool xy(double x,double y)
{
return x<y-eps;
}
bool dyd(double x,double y)
{
return x>y-eps;
}
bool xyd(double x,double y)
{
return x<y+eps;
}
bool dd(double x,double y)
{
return fabs(x-y)<eps;
} double crossProduct(point a,point b,point c)
{
return (c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x);
} point IntersectPoint(point u1,point u2,point v1,point v2)
{
point ans=u1;
double t = ((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x))/
((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x));
ans.x += (u2.x-u1.x)*t;
ans.y += (u2.y-u1.y)*t;
return ans;
} double Area(point p[],int n)
{
double ans=0.0;
p[n]=p[];
point tmp;
tmp.x=,tmp.y=;
for(int i=; i<n; i++)
{
ans += crossProduct(tmp,p[i],p[i+]);
}
return ans/2.0;
} void changeWise(point p[],int n)
{
for(int i=; i<n/; i++)
swap(p[i],p[n-i-]);
} double dist(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
/*
bool cmp(point a,point b)
{
double tmp=crossProduct(p[0],a,b);
if(dd(tmp,0.0))
return dy(dist(p[0],a),dist(p[0],b));
return xy(tmp,0.0);
} point Getsort(int n)
{
int tmp=0;
for(int i=1; i<n; i++)
{
if(xy(p[i].x,p[tmp].x) || dd(p[i].x,p[tmp].x)&&xy(p[i].y,p[tmp].y))
{
tmp=i;
}
}// printf("%d^^",tmp);
swap(p[0],p[tmp]);
sort(p+1,p+n,cmp);
}
*/
void cut(point p[],point s[],int n,int &len)
{
point tp[MAXX];
p[n]=p[];
for(int i=; i<=n; i++)
{
tp[i]=p[i];
}
int cp=n,tc;
for(int i=; i<n; i++)
{
tc=;
for(int k=; k<cp; k++)
{
if(xyd(crossProduct(p[i],p[i+],tp[k]),0.0))
s[tc++]=tp[k];
if(xy(crossProduct(p[i],p[i+],tp[k])*
crossProduct(p[i],p[i+],tp[k+]),0.0))
s[tc++]=IntersectPoint(p[i],p[i+],tp[k],tp[k+]);
}
s[tc]=s[];
for(int k=; k<=tc; k++)
tp[k]=s[k];
cp=tc;
}
len=cp;
} int main()
{
int t,n,m,i,j;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=; i<n; i++)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
}
double tmp=Area(p,n);
if(dy(tmp,0.0))
changeWise(p,n);
//point tmp=IntersectPoint(p[0],p[1],p[2],p[3]);
//printf("%lf %lf\n",tmp.x,tmp.y);
//Getsort(n);for(i=0; i<n; i++)printf("%lf**%lf*\n",p[i].x,p[i].y);
int len;
cut(p,s,n,len);//for(i=0; i<len; i++)printf("%lf==%lf=\n",s[i].x,s[i].y);
double area=Area(s,len);
printf("%.2lf\n",fabs(area));
}
return ;
}
poj 1279 -- Art Gallery (半平面交)的更多相关文章
- POJ 1279 Art Gallery 半平面交/多边形求核
http://poj.org/problem?id=1279 顺时针给你一个多边形...求能看到所有点的面积...用半平面对所有边取交即可,模版题 这里的半平面交是O(n^2)的算法...比较逗比.. ...
- POJ 1279 Art Gallery 半平面交求多边形核
第一道半平面交,只会写N^2. 将每条边化作一个不等式,ax+by+c>0,所以要固定顺序,方便求解. 半平面交其实就是对一系列的不等式组进行求解可行解. 如果某点在直线右侧,说明那个点在区域内 ...
- POJ 1279 Art Gallery(半平面交)
题目链接 回忆了一下,半平面交,整理了一下模版. #include <cstdio> #include <cstring> #include <string> #i ...
- POJ 1279 Art Gallery 半平面交 多边形的核
题意:求多边形的核的面积 套模板即可 #include <iostream> #include <cstdio> #include <cmath> #define ...
- poj 1279 Art Gallery - 求多边形核的面积
/* poj 1279 Art Gallery - 求多边形核的面积 */ #include<stdio.h> #include<math.h> #include <al ...
- poj 1279 Art Gallery (Half Plane Intersection)
1279 -- Art Gallery 还是半平面交的问题,要求求出多边形中可以观察到多边形所有边的位置区域的面积.其实就是把每一条边看作有向直线然后套用半平面交.这题在输入的时候应该用多边形的有向面 ...
- POJ 1279 Art Gallery(半平面交求多边形核的面积)
题目链接 题意 : 求一个多边形的核的面积. 思路 : 半平面交求多边形的核,然后在求面积即可. #include <stdio.h> #include <string.h> ...
- [POJ]1279: Art Gallery
题目大意:有一个N边形展馆,问展馆内有多少地方可以看到所有墙壁.(N<=1500) 思路:模板题,半平面交求出多边形的核后计算核的面积. #include<cstdio> #incl ...
- POJ 1279 Art Gallery【半平面交】(求多边形的核)(模板题)
<题目链接> 题目大意: 按顺时针顺序给出一个N边形,求N边形的核的面积. (多边形的核:它是平面简单多边形的核是该多边形内部的一个点集该点集中任意一点与多边形边界上一点的连线都处于这个多 ...
随机推荐
- 作为WEB工程师,我们是不是应该积极的推进一下用户浏览器的使用体验?
为什么会写这篇文章,其实是有原因的.目前我工作的公司的Web网站仅支持IE8以上的版本,然后我们经常接到客户的反馈,说为什么在他浏览器当中flash怎么显示不了,或者为什么在他浏览器中有这样那样的问题 ...
- cornerstone的简单使用
第一步打开工具点击左下角那个加号,弹出的选项中选Add Repository..或者直接点中间显示的Add Repository...是一样的 第二步: 下面填的内容是你经理给你的账号和密码,你只要c ...
- android 在应用中切换语言
场景: 在设置中切换中英文,然后跳转MainActivity....步骤: 1.在MyApplication 中初始化语言 public class MyApplication extends App ...
- SURF
推荐:http://www.cnblogs.com/tornadomeet/archive/2012/08/17/2644903.html SURF-Speeded Up Robust Feature ...
- java事务的类型——面试被问到
Java事务的类型有三种:JDBC事务.JTA(Java Transaction API)事务.容器事务. 1.JDBC事务 JDBC 事务是用 Connection 对象控制的.JDBC Conne ...
- [HTML]DIV+CSS 文字垂直居中
在说到这个问题的时候,也许有人会问CSS中不是有vertical-align属性来设置垂直居中的吗?即使是某些浏览器不支持我只需做少许的CSS Hack技术就可以啊!所以在这里我还要啰嗦两句,CSS中 ...
- Oracle找出非数字
可以这样判断: select translate('99999999999999', '\1234567890', '\') from dual; 返回的是空 select translate(' ...
- JS获取非行间样式
我们都知道用offset函数获取元素样式是一件很方便的事,但是offset只能获取行间样式,而无法获得非行间样式,这是它的瓶颈所在. 我们都知道js获取行间样式的方法,那么js是如何获取行距样式的呢? ...
- Unity-Animator深入系列---剪辑播放后位置预判(Animator.Target)
回到 Animator深入系列总目录 animator.SetTarget(...);可以在播放前预判剪辑播放后的位置,但只限于人形动画 参数1是预判的关节,参数2是映射的剪辑时间 调用后通过targ ...
- mediastream2使用指南(转载)
http://blog.sina.com.cn/s/blog_59d649610100diui.html 定义 Filter: 媒体库中处理数据的组件.一个filter有0到数个输入流和0到数个输出流 ...
