B-树

定义：

　　B-树是一种平衡的多路查找树，在文件系统中有所应用。主要用作文件的索引。

特性：（M为层数）

　　1.定义任意非叶子结点最多只有M个儿子；且M>2；

　　2.根结点的儿子数为[2, M]；

　　3.除根结点以外的非叶子结点的儿子数为[M/2, M]；

　　4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字,根节点至少一个关键字）；

　　5.非叶子结点的关键字个数=指向儿子的指针个数-1；

　　6.非叶子结点的关键字：K[1], K[2], …, K[m-1]，m<M+1；且K[i]< K[i+1] ；

　　7.非叶子结点的指针：P[1], P[2], …, P[m]；其中P[1]指向关键字小于K[1]的子树，P[m]指向关键字大于K[m-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

　　8.所有叶子结点位于同一层；

 

时间复杂度：（M为设定的非叶子结点最多子树个数，N为关键字总数）

　　　

 

基本操作：

     1.B-树的插入操作(重点判断是否满足n<=m-1)

　　　　a.利用前述的B-树的查找算法查找关键字的插入位置。若找到，则说明该关键字已经存在，直接返回。否则查找操作必失败于某个最低层的非终端结点上。

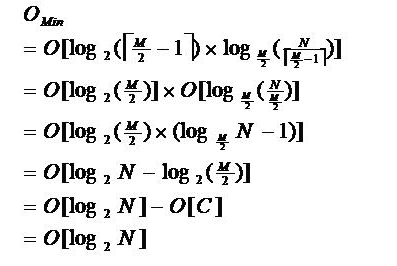
　　b.判断该结点是否还有空位置。即判断该结点的关键字总数是否满足n<=m-1。若满足，则说明该结点还有空位置，直接把关键字k插入到该结点的合适位置上。若不满足，说明该结点己没有空位置，需要把结点分裂成两个。　

　　　　分裂的方法是：生成一新结点。把原结点上的关键字和k按升序排序后，从中间位置把关键字（不包括中间位置的关键字）分成两部分。左部分所含关键字放在旧结点中，右部分所含关键字放在新结点中，中间位置的关键字连同新结点的存储位置插入到父结点中。如果父结点的关键字个数也超过（m-1），则要再分裂，再往上插。直至这个过程传到根结点为止。

　　（2）B-树的删除操作(重点判断删除所在结点及其兄弟结点，父结点中n>ceil(m/2)-1，n=ceil(m/2)-1，n<ceil(m/2)-1)

　　　　　　方法：在B-树上删除关键字K的过程也可以分为两步完成

　　　　　　a.利用前述的B-树的查找算法找出该关键字所在的结点。然后根据 k所在结点是否为叶子结点有不同的处理方法。

　　　　　　b.若该结点为非叶结点，且被删关键字为该结点中第i个关键字key[i]，则可从指针son[i]所指的子树中找出最小关键字Y，代替key[i]的位置，然后在叶结点中删去Y。因此，把在非叶结点删除关键字k的问题就变成了删除叶子结点中的关键字的问题了。

　　　　在B-树叶结点上删除一个关键字的方法是

　　　　　　首先将要删除的关键字 k直接从该叶子结点中删除。然后根据不同情况分别作相应的处理，共有三种可能情况：

　　　　　　a.如果被删关键字所在结点的原关键字个数n>=ceil(m/2)，说明删去该关键字后该结点仍满足B-树的定义。这种情况最为简单，只需从该结点中直接删去关键字即可。

　　　　　　b.如果被删关键字所在结点的关键字个数n等于ceil(m/2)-1，说明删去该关键字后该结点将不满足B-树的定义，需要调整。

　　　　　调整过程为：如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的右（左）兄弟结点中的关键字数目大于ceil(m/2)-1。则可将右（左）兄弟结点中最小（大）关键字上移至双亲结点。而将双亲结点中小（大）于该上移关键字的关键字下移至被删关键字所在结点中。

　　　　　　c.如果左右兄弟结点中没有“多余”的关键字，即与该结点相邻的右（左）兄弟结点中的关键字数目均等于ceil(m/2)-1。这种情况比较复杂。需把要删除关键字的结点与其左（或右）兄弟结点以及双亲结点中分割二者的关键字合并成一个结点,即在删除关键字后，该结点中剩余的关键字加指针，加上双亲结点中的关键字K_i一起，合并到A_i（即双亲结点指向该删除关键字结点的左（右）兄弟结点的指针）所指的兄弟结点中去。如果因此使双亲结点中关键字个数小于ceil(m/2)-1，则对此双亲结点做同样处理。以致于可能直到对根结点做这样的处理而使整个树减少一层。

　　　　总之，设所删关键字为非终端结点中的Ki，则可以指针Ai所指子树中的最小关键字Y代替Ki，然后在相应结点中删除Y。对任意关键字的删除都可以转化为对最下层关键字的删除。

如图示：

a、被删关键字Ki所在结点的关键字数目不小于ceil(m/2)，则只需从结点中删除Ki和相应指针Ai，树的其它部分不变。

b、被删关键字Ki所在结点的关键字数目等于ceil(m/2)-1，则需调整。调整过程如上面所述。

c、被删关键字Ki所在结点和其相邻兄弟结点中的的关键字数目均等于ceil(m/2)-1，假设该结点有右兄弟，且其右兄弟结点地址由其双亲结点指针Ai所指。则在删除关键字之后，它所在结点的剩余关键字和指针，加上双亲结点中的关键字Ki一起，合并到Ai所指兄弟结点中（若无右兄弟，则合并到左兄弟结点中）。如果因此使双亲结点中的关键字数目少于ceil(m/2)-1，则依次类推.